Relations and rectangular coordinate system

RELATIONS AND THE RECTANGULAR COORDINATE SYSTEM

Many things in daily life are related. For example, a student’s grade in a course usually is related to the amount of time spent studying, while the number of miles per gallon of gas used on a car trip depends on the speed of the car. Driving at 55 mph might give 31 miles per gallon, while driving at 65 mph might reduce the gas mileage to 28 miles per gallon.

     Pairs of related numbers, such as 55 and 31 or 65 and 28 in the gas mileage illustration, can be written as ordered pairs. An ordered pair of numbers consists of two numbers, written inside parentheses, in which the sequence of the numbers is important. For example, (4, 2) and (2, 4) are different ordered pairs because the order of the numbers is different. Notation such as (3, 4) has already been used in this book to show an interval on the number line. Now the same notation is used to indicate an ordered pair of numbers. In virtually every case, the intended use will be clear from the context of the discussion.

RELATIONS  A set of ordered pairs is called a relation. The domain of a relation is the set of first elements in the ordered pairs, and the range of the relation is the set of all possible second elements. In the driving example above, the domain is the set of all possible speeds and the range is the set of resulting miles per gallon. In this text, we confine domains and ranges to real number values.

  Ordered pairs are used to express the solutions of equations in two variables.

For example, we say that (1, 2) is a solution of 2x -y = 0, since substituting 1 for x and 2 for y in the equation gives

                                      2(1)-2=0
                                                    0=0

a true statement. When an ordered pair represents the solution of an equation with the variables x and y, the y-value is written first.

   Although any set of ordered pairs is a relation, in mathematics we are most interested in those relations that are solution sets of equations. We may say that an equation defines a relation, or that it is the equation of the relation. For simplicity, we often refer to equations such as

                           y=3x+5 or x^2 + y^2 = 16
as relations, although technically the solution set of the equation is the relation.

Example 1 FINDING ORDERED PAIRS, DOMAINS, AND RANGES

For each relation defined below, give three ordered pairs that belong to the relation, and state the domain and the range of the relation.
 (a) {(2, 5), (7, -1), (10, 3), (-4, 0), (0, 5)}

Three ordered pairs from the relation are any three of the five ordered pairs in the set. The domain is the set of first elements,
                              {2, 7, 10, -4, 0},
and the range is the set of second elements,
                                   {5, -1, 3, 0},

(b) y= 4x - 1

  To find an ordered pair of the relation, choose any number for x or y and substitute in the equation to get the corresponding value of the other variable. For ex-
ample, let x=-2. Then

                          y = 4(-2) -1= -9,

giving the ordered pair (-2, -9). If y = 3, then

                                       3=4x-1

                                        4=4x

                                        1 =x,
and the ordered pair is (1, 3). Verify that (0, -1) also belongs to the relation. Since x and y can take any real-number values, both the domain and range are (-inf,inf),

(c) x=root(y-1)

  Verify that the ordered pairs (1,2), (0, 1), and (2,5) belong to the relation. Since x equals the principal square root of y - 1, the domain is restricted to (0,inf). Also, only non-negative numbers have a real Square root, so the range is determined by the inequality

                                           y-1>=0

                                                 y>=1,

giving (1,inf) as the range. 

THE RECTANGULAR COORDINATE SYSTEM  Since the study of relations often involves looking at their graphs, this section includes a brief review of the coordinate plane. As mentioned in Chapter 1, each real number corresponds to a point on a number line. This correspondence is set up by establishing a coordinate system for the line. This idea is extended to the two dimensions of a plane by drawing two perpendicular lines, one horizontal and one vertical. These lines intersect at a point o called the origin. The horizontal line is called the x-axis, and the vertical line is called the y-axis.

      Starting at the origin, the x-axis can be made into a number line by placing positive numbers to the right and negative numbers to the left. The y-axis can be made into a number line with positive numbers going up and negative numbers going down.

The x-axis and y-axis together make up a rectangular coordinate system, or Cartesian coordinate system (named for one of its co-inventors, René Descartes; the other co-inventor was Pierre de Fermat). The plane into which the coordinate system is introduced is the coordinate plane, or xy-plane. The x-axis and y-axis divide the plane into four regions, or is quadrants, labeled as shown in Figure 3.1. The points on the x-axis and y-axis belong to no quadrant.

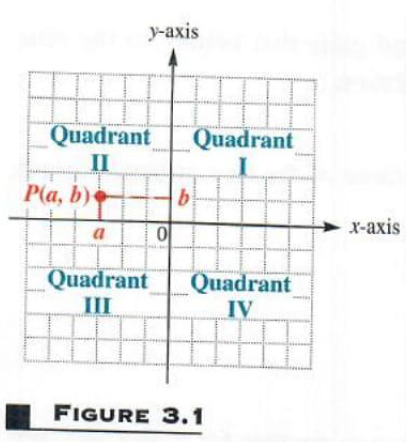
Each point P in the xy-plane corresponds to a unique ordered pair (a, b) of real numbers. The numbers a and b are the coordinates of point P. To locate on the xy-plane the point corresponding to the ordered pair(3, 4), for example, draw a vertical line through 3 on the x-axis and a horizontal line through 4 on the y-axis. These two lines cross at point A in Figure 3.2. Point A corresponds to the ordered pair (3, 4). Also in Figure 3.2, B corresponds to the ordered pair (-5, 6), C to (-2, -4), D to (4, -3), and E to (-3, 0). The point Pcorresponding to the ordered pair (a, b) often is written as P(a, b) as in Figure 3.1 and referred to as “the point (a, b).”

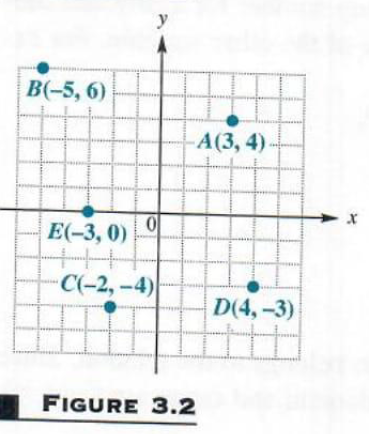
As we shall see later in this chapter the graph of a relation is the set of points in the plane that corresponds to the ordered pairs of the relation.

Two formulas, the distance and midpoint formulas, will be useful in our study of relations in this chapter.

THE DISTANCE FORMULA  By using the Pythagorean theorem, we can develop a formula to find the distance between any two points in a plane. For example, Figure 3.3 shows the points P(-4, 3) and R(8, -2).

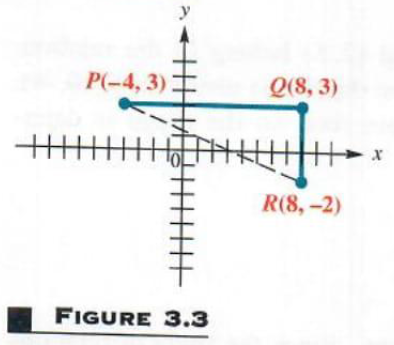
To find the distance between these two points, complete a right triangle as shown in the figure. This right triangle has its 90° angle at (8, 3). The horizontal side of the triangle has length

                                     |8 - (-4)| =12,

where absolute value is used to make sure that the distance is not negative. The vertical side of the triangle has length
                                       |3 - (-2)| = 5
By the Pythagorean theorem, the length of the remaining side of the triangle is
           root(12^2+5^2)=root(144+25)=root(169)=13
The distance between (-4,3) and (8,-2) is 13.

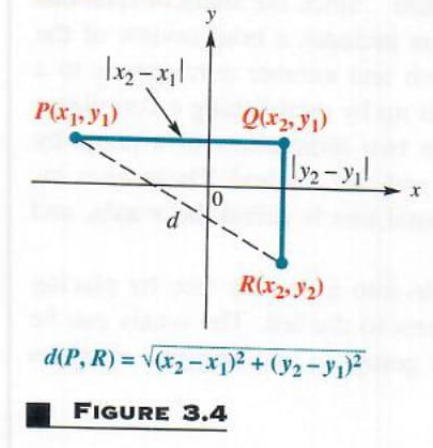
  To obtain a general formula for the distance between two points on a coordinate plane, let P(x_1, y_1) and R(x_2,y_2) be any two distinct points in a plane, as shown in Figure 3.4. Complete a triangle by locating point Q with coordinates (x_2,y_1). Using the Pythagorean theorem gives the distance between P and R, written d(P,R), as

                  d(P,R)=root((x_2-x_1)^2+(y_2-y_1)^2   

NOTE The use of absolute value bars is not necessary in this formula, since for all real numbers a and b, |a-b|^2 =(a-b)^2.
The distance formula can be summarized as follows.

DISTANCE FORMULA  Suppose that P(x_1, y_1) and R(x_2,y_2) are two points in a coordinate plane. Then the distance between P and R, written d(P,R), is given by the distance formula                                                                           d(P,R)=root((x_2-x_1)^2+(y_2-y_1)^2 

Although the proof of the distance formula assumes that P and R are not on a horizontal or vertical line, the result is true for any two points.

Example 2 USING THE DISTANCE FORMULA

Find the distance between P(-8,4) and Q(3,-2).
According to the distance formula,

  d(P,Q)=root([3-(-8)^2]+(-2-4)^2                                  x_1=-8,y_1=4,x_2=3,y_2=-2

                      =root(11^2+(-6)^2

                      =root(121+36)=root(157)

NOTE As shown in Example 2, it is customary to leave the distance between two points in radical form rather than approximating it with a calculator (unless, of course, it is otherwise specified).

  A statement of the form “If p, then q” is called a conditional statement. The related statement “If q, then p” is called its converse. In Chapter 2 we studied the Pythagorean theorem. The converse of the Pythagorean theorem is also a true statement: If the sides a, b, and c of a triangle satisfy then the triangle is a right triangle with legs having lengths a and b and hypotenuse having length c. This can be used to determine whether three points are the vertices of a right triangle, as shown in the next example.

Example 3 DETERMINING WHETHER THREE POINTS ARE THE VERTICES OF A RIGHT TRIANGLE 

Are the three points M(-2,5), N(12,3), and , M(10,-11) the vertices of a right triangle? 
  A triangle with the three given points as vertices is shown in Figure 3.5. This triangle is a right triangle if the square of the length of the longest side equals the sum of the squares of the lengths of the other two sides. Use the distance formula to find the length of each side of the triangle.
                    

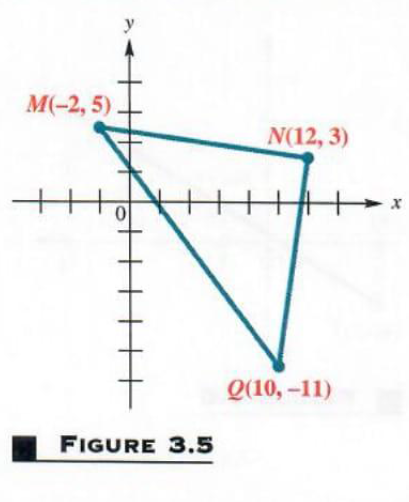
d(M,N)=root([12-(-2)^2]+(3-5)^2)=root(196+4)=root(200)                                                                                                                                                                             d(M,Q)=root([10-(-2)^2]+(-11-5)^2)=root(144+256)=root(400)=20                                                                                                                                                                                                                                                                    d(N,Q)=root((10-12)^2+(-11-3)^2)=root(4+196)=root(200)

By these results,              

             [d(M,Q)]^2=[d(M,N)]^2+[d(N,Q)]^2

since 20^2=root(200)+root((200)^2), or 400=400, is a true Statement.

This proves that the triangle is a right triangle with hypotenuse connecting M and Q.
    Using a procedure similar to that of Example 3, it can be determined whethe three points lie on a Straight line. Points that lie on a line are called collinear. Three points are collinear if the sum of the distances between two Pairs of the points is equal to the distance between the remaining pair of points.

Example 4 DETERMINING WHETHER THREE POINTS ARE COLLINEAR

Are the points (-1, 5), (2, -4), and (4, -10) collinear?

 The distance between (-1, 5) and (2, -4) is

root((-1-2)^2+[5-(-4)]^2)=root(9+81)=root(90)=3root(10)

 The distance between (2, -4) and (4, -10) is

root((2-4)^2+[-4-(-10)]^2)=root(4+36)=root(40)=2root(10)

Finally, the distance between the remaining pair of points, (-1, 5) and (4, -10)is

root((-1-4)^2+[5-(-10)]^2)=root(25+225)=root(250)=5root(10)

Because 3root(10)+2root(10)=5root(10), the three points are collinear. 

THE MIDPOINT FORMULA  The midpoint formula is used to find the coordinates of the midpoint of a line segment. (Recall that the midpoint of a line segment is equidistant from the endpoints of the segment.) To develop the midpoint formula, let (x_1,y_1) and (x_2,y_2) be any two distinct points in a plane. (Although Figure 3.6 shows (x_1<y_2), no particular order is required.) Assume that the two points are not on a horizontal or vertical line. Let (x,y) be  the midpoint of the segment connecting (x_1,y_1) and (x_2,y_2). Draw vertical lines from each of the three points to the x-axis, as shown in Figure 3.6.
  Since (x,y) is the midpoint of the line segment connecting (x_1,y_1)
and (x_2,y_2), the distance between x and x_1, equals the distance between x and x_2 so that

                                       x_2-x=x-x_1

                                          x_2+x_1=2x

                                           x=(x_1+x_2)/2

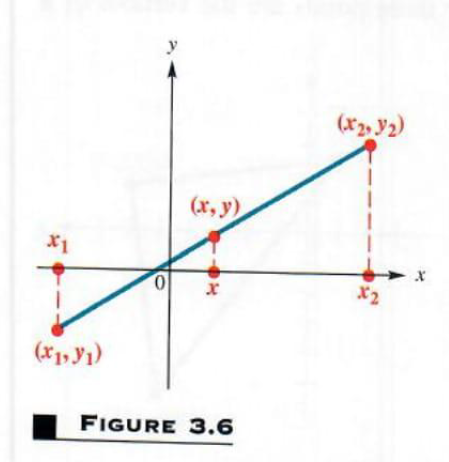
By this result, the x-coordinate of the midpoint is the average of the -coordinates of the endpoints of the segment. In a similar manner, the y-coordinate of the midpoint is (y_1+y_2)/2, proving the following statement.

MIDPOINT FORMULA The midpoint of the line segment with endpoints (x_1,y_1)) and (x_2,y_2) is

                         ((x_1+x_2)/2,(y_1+y_2)/2)

In other words, the midpoint formula says that the coordinates of the midpoint of a segment are found by calculating the average of the x-coordinates and the average of the y-coordinates of the endpoints of the segment. In Exercise 43, you are asked to verify that the coordinates above satisfy the definition of midpoint.

Example 5  : USING THE MIDPOINT FORMULA

Find the midpoint M of the segment with endpoints(8, -4)  and (-9, 6).
Use the midpoint formula to find that the coordinates of M are

                          (8+(-9))/2,(-4+6)/2)=(-1/2,1)

Example 6 USING THE MIDPOINT FORMULA 

A line segment has an endpoint at (2, -8)and midpoint at (-1, -3)Find the other endpoint of the segment.

The formula for the x-coordinate of the midpoint is (x_1+x_2)/2. Here the x-coordinate of the midpoint is -1. Letting x_1=2 gives

                                    -1=(2+x_2)/2

                                    -2=2+x_2             

                                    -4=x_2

In the same way,y_2=2 and the endpoint is (-4,2).