Using equations and inequalities to solve algebra story problems
NUMBER RELATION PROBLEMS
OBJECTIVES
Upon completing this section you should be able to:
- Identify a problem as being a number relation problem.
- Express relationships between unknowns and determine an equation to solve a number relation problem.
- Apply formulas to solve certain types of number relation problems.
Read the following three problems carefully:
- Jim is two years older than Sue and four years younger than Hugh. The sum of their ages is 59. Find the age of each.
- The length of rope is 59 meters. It is cut in three pieces such that the first is two meters longer than the second and four meters shorter than the third. Find the length of each piece.
- There are three numbers such that the first is two more than the second and four less than the third. If their sum is 59, find the numbers.
At first glance these may seem to be three different problems. However, closer examination shows that they are actually the same. For all three a possible outline is
The equation (x + 2) + (x) + (x + 6) = 59 will lead to the solutions.
Problems such as these are classified as number relation problems. If you recognize a problem in this class, then the outline for solving it must show a relation between the numbers. The equation will then be based on a statement about the sum, difference, and so on.
The problems you solved in the last section were all number relation problems. They all involved comparing two or more numbers.
| Again, x does not have to be used to represent the second number. It could be used to represent one of the other numbers. We would then have a different set of expressions for the three numbers. Work this problem if x = first first number = 19 |
Problems comparing age, height, weight, and so forth are number relation problems.
| Work this problem if x = Janet's age. |
The field of business contains number relation problems.
| Remember the five steps in solving a verbal problem. |
Example 4 A customer purchases a stereo radio for $306.80, including a 4% sales tax. Find the price of the radio and the amount of sales tax.
Solution
If x represents the price of the radio, then the sales tax is found by multiplying the price of the radio by 4%. Thus, we have
| Note the tax is on the price of the radio and not on $306.80. |
Then the total sale is the sum of the price of the radio and the sales tax.
x + .04x = 306.80
| Remember, to change a percent to a decimal divide by 100. |
Solving the equation, we obtain
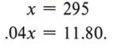
| Solve the equation x + .04x = 306.80 here in the margin. It will give you practice in solving equations involving decimals. |
Check: The total of $295.00 and $11.80 is $306.80.
Some number relation problems require prior knowledge of a formula to set up the equation.
Example 5 In a certain rectangle the length is two more than the width. If the length is increased by three and the width by two, the perimeter of the new rectangle will be twice that of the original. Find the length and width of the original rectangle.
Solution
Notice that to solve the problem, you must know that P = 2l + 2w is the formula for the perimeter of a rectangle. We outline this as
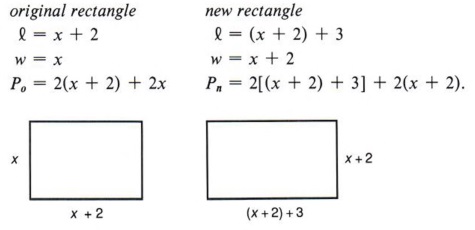
| The perimeter of a rectangle is twice the length added to twice the width. |
| Re-read the original problem to see if the expression for the dimensions of the two rectangles make sense. |
Notice that we used subscripts o and n to distinguish the original perimeter from the new perimeter. The equation comes from the statement that 
| Po represents the original perimeter. Pn represents the new perimeter. Recall the order of operations in removing grouping symbols. |
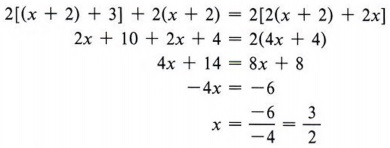
Since x represents the width, we have
Thus, the perimeter of the new rectangle is twice that of the original rectangle, and the answer checks.
| Again, just solving for x does not solve the problem. Once the length and width are determined, the check will tell if they are correct. |
Example 6 An individual invests $8,000 for one year. Part is invested at 6% and the rest at 5%. If the total interest at the end of the year is $460, how much was invested at each rate?
Solution
Here we must use the interest formula I = prt, where I represents the interest, r represents the rate of interest, p represents the principal amount invested, and t is the time in years. We let x = amount invested at 5% and 8,000 - x = amount invested at 6%. Then, the interest earned at 5% is
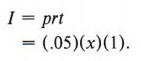
The rate of interest r is expressed as a decimal number. Change 5% to a decimal number. |
The interest earned at 6% is
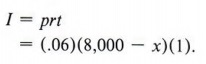
The equation representing the total interest is
.05x + .06(8,000 - x) = 460.
Solving the equation gives
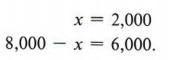
Thus, $2,000 was invested at 5% and $6,000 at 6%.
Check: 5% of $2,000 is $100 and 6% of $6,000 is $360. The two interest amounts total $460.
Notice that it is important that (8,000 - x) be enclosed in parentheses since 6% is multiplying the entire expression. |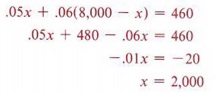
Example 7 The interest due on a two-year $300 loan amounted to $90. What annual rate of interest was charged?
Solution
Again, the formula I = prt is useful. Here I = $90, p = $300, and t = 2 years. Therefore,
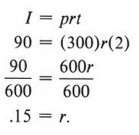
Thus, the rate of interest was 15%.
Check: $300 at 15% for 2 years yields $90 interest.
Percent problems come in three basic forms. Each is easily translated to algebraic equations as shown below.
|
DISTANCE-RATE-TIME PROBLEMS
OBJECTIVES
Upon completing this section you should be able to:
- Identify distance-rate-time problems.
- Apply the distance formula to solve problems in this group.
Another formula often found in verbal problems is
d = rt (distance = rate X time),
which is the distance formula for constant rate. Given the rate at which an object is moving and the time that it moves at this rate, we can find the distance the object moves.
Example 1 A car travels at the rate of 55 mph for four hours. How far does it travel?
Solution
Using the formula d = rt, substitute r = 55 and t = 4, obtaining
d = (55)(4) = 220.
Thus, the distance traveled is 220 miles.
| How far would the car travel in one hour? In two hours? In three hours? |
If the distance and rate are both given, we can find the time.
Example 2 How long will it take a plane whose ground speed is 530 mph to travel 2,120 miles?
Solution
In this case, let d = 2,120 and r = 530 in the formula
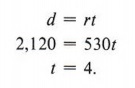
It will therefore take four hours to travel the distance.
| Always check to see that the units agree. That is, if the speed is given in miles per hour then the distance must also be in miles. |
We can also solve for the rate if we are given the distance and time.
Example 3 A person walked 21 miles in 
hours. What was the person's average rate?
Solution
We substitute d = 21 and t = 3.5 in the formula
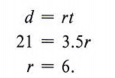
The person's average rate was six miles per hour.
One type of distance problem involves two objects leaving from the same point and traveling in the same direction.
You could also leave the time in fraction form. Then |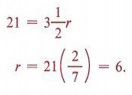
Example 4 A bank robber leaves town heading north at an average speed of 120 kilometers per hour. The sheriff leaves two hours later in a plane that travels at 200 kilometers per hour. How long will it take the sheriff to catch the robber?
Solution
We outline as follows:
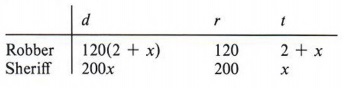
In this table x represents the time the sheriff takes to catch the robber. Notice that the distance 120(x + 2) and 200x come from the formula d = rt.
| Use a table such as this one when two or more moving objects are involved. It allows for easy comparisons. |
The equation comes from the fact that the sheriff and the robber will have traveled the same distance when the sheriff catches the robber. Thus,
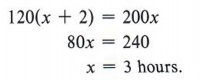
The sheriff will catch the robber in three hours.
| Notice that since the sheriff left two hours later, the robber will have been on the run for x + 2 hours when he is caught. When the sheriff catches the robber, they will each have traveled the same distance. |
Check: The bank robber has traveled for five hours at 120 km/ hr for a distance of 5(120) = 600 km.
The sheriff has traveled for three hours at 200 km/hr for a distance of 3(200) = 600 km.
Another type of distance problem involves two objects leaving from the same point and traveling in opposite directions.
Example 5 Pamela and Sue start at the same point and walk in opposite directions. The rate at which they are moving away from one another is 11 mph. At the end of three hours Pamela stops and Sue continues to walk for another hour. At the end of that time Pamela has walked twice as far as Sue. How far apart are they?
Solution
We use the following table:
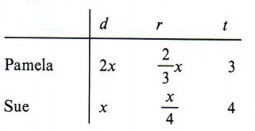
The problem tells us the time and lets us represent the distance. To represent the value for r we divide the distance by the time.  |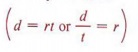
The sum of their rates is 11 mph.
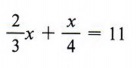
Solving, we obtain
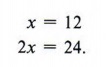
Thus, they are 36 miles apart.
Check: Pamela's rate is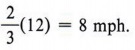 
Sue's rate is 
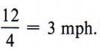Their total rate is 11 mph. Also, Pamela's distance (24) is twice Sue's distance (12).
| Again, check to make sure the answers agree with the original problem. |
Still another type of distance problem involves two objects that leave from two different points and travel toward each other.
Example 6 Juan and Steven started 36 miles apart and walked toward each other, meeting in three hours. If Juan walked two miles per hour faster than Steven, find the rate of each.
Solution
| If we let x represent the rate at which Steven walked, then Juan's rate would be represented by x + 2. |
First set up the following table:
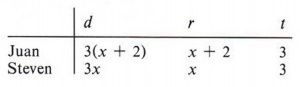
| We represent the distance as the product of the rate and time (d = rt). |
The total distance they have traveled is 36 miles. Thus,
3(x + 2) + 3x = 36.
Solving, we obtain
x = 5
x + 2 = 7.
The answers are
Juan's rate = 7 mph
Steven's rate = 5 mph.
Check: Juan's rate (7) is two miles per hour faster than Steven's (5). Also 3(7) + 3(5) = 21 + 15 = 36.
Within the class of problems using d = rt is a subclass of problems concerned with parallel and opposing forces.
Parallel forces travel in the same direction, and opposing forces travel in opposite directions. The normal speed of the plane will be reduced by the speed of the wind. |
Example 7 A plane, whose speed in still air is 550 mph, flies against a headwind of 50 mph. How long will it take to travel 1,500 miles?
Solution
We use the formula d = rt. The distance is 1,500 miles and the rate of the plane against the wind will be its still air speed (550 mph) reduced by the headwind (50 mph).
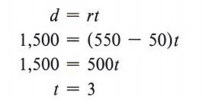
Thus, it will take three hours to travel the distance.
Check: 3(550 - 50) = 3(500) = 1,500
Example 8 Mike can row his boat from the hunting lodge upstream to the park in five hours. He can row back from the park to the lodge downstream in three hours. If Mike can row x kilometers per hour in still water, and if the stream is flowing at the rate of two kilometers per hour, how far is it from the lodge to the park?
Solution
In working the problem we assume that the rate of the stream will increase or decrease the rate of the boat by two kilometers per hour. Since x represents Mike's speed in still water, we obtain
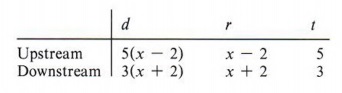
Setting the distance upstream equal to the distance downstream, we obtain
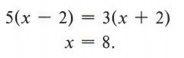
Notice that x is not the solution to the problem but is Mike's rate of rowing in still water. However, the question asked is "What is the distance from the lodge to the park?" To answer this use either the distance upstream or downstream since they are the same. Using the upstream distance, we have
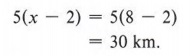
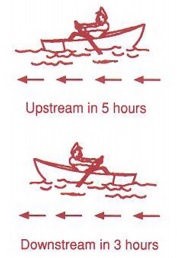
| When Mike is rowing upstream, he is opposing the direction of the current. When he rows downstream, he is parallel to the stream's current. |
| See if you get the same answer using the distance downstream. |
MIXTURE PROBLEMS
OBJECTIVES
Upon completing this section you should be able to:
- Identify mixture problems.
- Construct an outline which allows for easy comparison of items and the formation of an equation.
- Find the solution to mixture problems.
The final type of problem we will discuss in this chapter is the mixture problem. Mixture problems come in various settings. They may involve mixing candy, coffee, coins, liquids, and so on. They all have a central concept however, which helps in solving them.
Example 1 A merchant has one brand of coffee that sells for $1.80 per pound and a second brand that sells for $2.20 per pound. The merchant wishes to make a blend of the two coffees. How many pounds of each price coffee must be used to make 20 pounds of a mixture that would sell for $ 1.90 per pound?
Solution
We set up the following table from the information given in the problem.
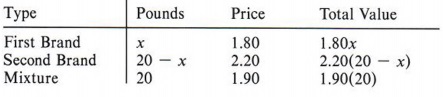
Looking at the "total value" column of the table, notice that the sum of the total values of the two brands must equal the total value of the mixture. This fact gives us the equation
1.80x + 2.20(20 - x) = 1.90(20).
| If x represents the number of pounds of the first brand, then 20 - x must represent the number of pounds of the second brand. |
Solving, we obtain
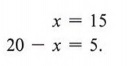
Thus, the merchant must use 15 pounds of the first brand and 5 pounds of the second brand.
| Always check your answers against the original problem. |
Example 2 A total of 100 coins in nickels and quarters has a value of $14.40. How many of each type of coin are there?
Solution
From the given information we set up the following table:
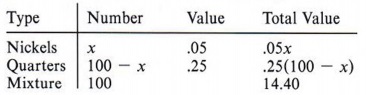
Looking at the "total value" column of the table, notice that theAgain we see that the sum of the total value of nickels and the total value of quarters is equal to the total value of the mixture ($14.40). We therefore write the equation
.05x + .25(100 - x) = 14.40.
| If there are x nickels and each nickel is worth $.05, then the total value of the nickels is .05x. |
Solving, we obtain
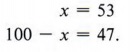
Thus, there are 53 nickels and 47 quarters.
Check: .05(53) + .25(47) = 2.65 + 11.75 = 14.40
Example 3 A merchant has three types of hard candy. The first sells for $1.10 per kilogram, the second for $1.50 per kilogram, and the third for $1.60 per kilogram. How many kilograms of each candy would be used to make 100 kilograms that would sell for $1.36 per kilogram, if twice as much of the second type must be used as the third?
Solution
We may outline as follows:
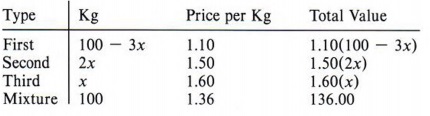
| Again, in this type of problem the use of a table will allow easy comparisons. |
Notice that the equation must come from the value column. Any equation must have like quantities on each side. You can never equate pounds with value, number of coins with the dollar value of the coins, and so forth.
| We can only compare like quantities. |
The equation is
1.10(100 - 3x) + 1.50(2x) + 1.60(x) = 136.
| Solve this equation. See if your answers agree. |
| Again the check provides the opportunity to see if the answers are correct. |
Example 4 How much pure alcohol must be added to nine quarts of water to obtain a mixture of 40% alcohol?
Solution
We set up the table.
| We could also work this problem equating water instead of alcohol. We would start with 9 quarts that are 100% water and end up with x + 9 quarts that are 60% water. Solve: 1.00(9) = .60(x + 9). |
Notice that the amount of alcohol in the mixture will be equal to the amount added. We can therefore write the equation
x = .40(x + 9).
Solving, we obtain
x = 6.
Therefore, six quarts of alcohol must be added.
Check: If we add 6 quarts to 9 quarts, there will be a total of 15 quarts in the mixture, of which 6 quarts, or 40%, is alcohol.
Example 5 The capacity of a car's radiator is nine liters. The mixture of antifreeze and water is 30% antifreeze. How much of the mixture in the radiator must be drawn off and replaced with pure antifreeze to raise the percentage of the mixture to 65% antifreeze?
Solution
| In this problem the number of liters of solution remains constant. Before we set up a table outline, we must decide whether to talk about antifreeze or water. |
In outlining this problem again keep in mind that the equation must equate like quantities. We can choose to make an equation equating antifreeze with antifreeze, or water with water, but not water with antifreeze. If we choose to equate antifreeze with antifreeze, we proceed as follows. If x represents the number of liters of the mixture to be drawn off, the outline would be:
| Do this problem again, equating water with water. Set up a similar table only this time label the heading water instead of antifreeze. Obtain the equation and solve it. Your answer should be the same. |
Note that the original amount of antifreeze, less the amount of antifreeze drained off, plus the amount of antifreeze added back will equal the final amount of antifreeze. Thus,
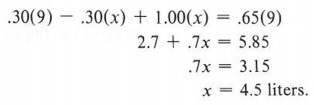
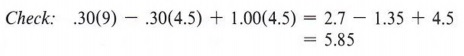
| In this case solving for x solves the problem. |
SUMMARY
Key Words
- An outline expresses all unknowns in a problem in terms of one unknown.
- Number relation problems involve comparing two or more numbers.
- Distance-rate-time problems involve the distance formula for a constant rate given by d = rt.
- Mixture problems involve combining quantities of various concentrations.
Procedures
- Translate from words to algebraic expressions to properly outline a word problem.
- Outline a problem completely and accurately before attempting to solve it.
- To solve a word problem follow these steps:
Step 1 Write an expression for the unknown.
Step 2 Write an equation that relates the unknowns to each other.
Step 3 Solve the equation.
Step 4 Make sure you have answered the question.
Step 5 Check your answers to make sure they agree with the original problem.