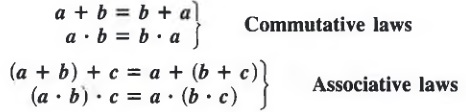WHOLE NUMBERS, FRACTIONS AND THEIR REPRESENTATION

NUMBERS AND THEIR GRAPHS

KINDS OF NUMBERS

The numbers we use to count things are called natural numbers. The numbers

are natural numbers, whereas 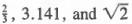are not.

A prime number is a natural number greater than 1 that is exactly divisible only by itself and 1 - that is, a multiple of no natural number other than itself and 1. For example,

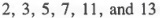
are prime numbers, whereas 4 and 21 are not since 4 is divisible by 2 and 21 is divisible by 7 and 3. We exclude 1 from the set of prime numbers for reasons we will explain later.

Example 1 Which of the following are prime numbers?
a. 5
b. 15
c. 29

Solution
a. 5 is prime (because it is exactly divisible only by 1 and itself).
b. 15 is not prime (because it is divisible by 3 and 5).
c. 29 is prime (because it is exactly divisible only by 1 and itself).

When the number 0 is included with the natural numbers, the numbers in the enlarged collection

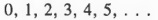
are called whole numbers. Thus, we can refer to numbers such as 2, 3, and 6 as natural numbers or whole numbers. Of course, we can also call 2 and 3 prime numbers.

The natural numbers 2, 4, 6, ... are called even numbers, and the natural numbers 1, 3, 5, ... are called odd numbers. The even numbers are always multiples of 2. (We can think of the whole number 0 as being even, since 0 is a multiple of 2.) A number is odd if it leaves a remainder 1 when it is divided by 2.

EQUALITY STATEMENTS

Statements about numbers such as 4 = 2 x 2, 7 - 2 + 3 = 8 and 6 + 5 = 11 are called equality statements. In an equality statement, the symbols on the left-hand side of the equals sign (=) name the same number as the symbols on the right-hand side. Thus, 4 and 2x2 name the same natural number, and 7 - 2 + 3 and 8 name the same number. We use the symbol # when the left-hand side does not equal the right-hand side. For example,

5 ≠ 2 x 2 and 7 - 3 ≠ 2.

NUMBER LINE

The whole numbers are ordered. That is, we can always say that a particular whole number is greater than, equal to, or less than another. We can use a number line to represent the relative order of a set of whole numbers.

To construct a number line:

1. Draw a straight line.
2. Decide on a convenient unit of scale and mark off units of this length on the line, beginning on the left.
3. On the bottom side of the line, label enough of these units to establish the scale, usually two or three points. The point representing 0 is called the origin.
4. Add a small arrow pointing to the right to indicate that numbers are larger to the right.
5. On the top side of the line, label the numbers to be graphed. Graph the numbers by placing dots at the appropriate places on the line.

Example 2 Graph the following numbers on a number line.
a. The prime numbers less than 8.
b. The first four natural numbers divisible by 2.

ORDER SYMBOLS

Given any two numbers, the number whose graph on a number line is to the left is less than the number whose graph is to the right. In Figure 1.1, the graph of 3 is to the left of the graph of 7. Therefore, 3 is less than 7. We could also state this relationship as "7 is greater than 3."

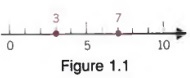
We use special symbols to indicate the order relationship between two numbers:

< means "is less than";
> means "is greater than."

For example,2 < 5 is read "2 is less than 5,"
and 5 > 2 is read "5 is greater than 2."

Note that the point of the symbols < and > always points to the smaller number.

Example 3 For the graph shown, replace the comma in each pair with the proper symbol: < , > , or = .

a. p, n
b. m, p
c. r, r

Solutions
a. p > n (The graph of p is to the right of the graph of n.)
b. m < p (The graph of m is to the left of the graph of p.)
c. r = r

SUMS AND PRODUCTS

Mathematics is a language. As such, it shares a number of characteristics with any other language. For instance, it has verbs, nouns, pronouns, phrases, sentences, and many other concepts that are normally associated with a language. They have different names in mathematics, but the ideas are similar.

In language, we use pronouns such as he, she, or it to stand in the place of nouns. In mathematics, we use symbols such as x, y, z, a, b, c, and the like, to stand in the place of numbers. Letters used in this way are called variables. In this chapter, variables will always represent whole numbers.

In a language, the verbs are action words, expressing what happens to nouns. In mathematics, operations such as addition, multiplication, subtraction, or division express an action involving numbers. The symbols we use for these operations, and the properties these operations have, are the same in algebra as in arithmetic.

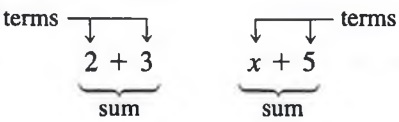
SUMS

When we add two numbers a and b, the result is called the sum of a and b. We call the numbers a and b the terms of the sum.

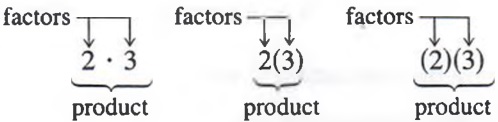
PRODUCTS

When we multiply two numbers a and b, the result is called the product of a and b. We call numbers a and b the factors of the product. In arithmetic, we used the symbol X to represent multiplication. But in algebra, the symbol x may sometimes be confused with the variable x, which we use so frequently. So in algebra we usually indicate multiplication either by a dot between the numbers or by parentheses around one or both of the numbers.

Multiplication of variables may be written the same way or may be written with the symbols side by side. For example,

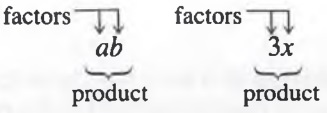
where

ab means "the number a times the number b," and
3x means "the number 3 times the number".

PRIME FACTORS

If we multiply 3 by 4, we obtain 12. We might also obtain 12 by multiplying the natural numbers 2 and 6, or 12 and 1, or 2, 2, and 3. In this book, we are interested primarily in the prime factors of a number. Prime factors are factors that are prime numbers. If we now ask for the prime factors of 12, we are restricted to the single set 2, 2, and 3. This is the reason we do not include 1 in the set of prime numbers. If 1 were included, another set of prime factors of 12 would be 1, 2, 2, and 3.

Example 1 Write each number as the product of prime factors.

a. 22 = 2 * 11
b. 21 = 3 * 7
c. 18 = 2 * 3 * 3
d. 45 = 5 * 3 * 3

PROPERTIES OF ADDITION AND MULTIPLICATION

A basic property of addition and multiplication, called the commutative law, states the following:

The order in which the terms of a sum (or factors of a product) are paired does not change the sum (or product).

Thus, it is always true that

and

Example 2 a. 5 + 3 = 3 + 5 by the commutative law.
b. 5 * 3 = 3 * 5 by the commutative law.

Another useful property of addition and multiplication, called the associative law, states the following:

The way in which three terms in a sum (or three factors in a product) are grouped for addition (or multiplication) does not change the sum (or product).

Thus, it is always true that

and

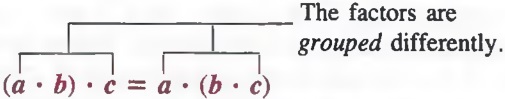
Example 3 a. (2 + 3) + 4 = 2 + (3 + 4) by the associative law.
b. 2 * (3 * 4) = (2 * 3) * 4 by the associative law.

In the above example, we used parentheses to indicate grouping. In (2 + 3) + 4, the parentheses indicated that die 2 and 3 are added first. In 2 + (3 + 4), the parentheses indicated that the 3 and 4 are added first. Brackets [ ] can be used in the same way that we use parentheses.

ALGEBRAIC EXPRESSIONS

An algebraic expression, or simply, an expression, is any meaningful collection of numbers, variables, and signs of operation. For example,
4x, 2 > x + y, and 2(x + 3)

are algebraic expressions. An important part of algebra involves translating word phrases into algebraic expressions.

Example 4

By the commutative law, 5 * y = y * 5 and 3 * (x + y) = (x + y) * 3. However, it is customary to write products with the numeral first.

DIFFERENCES AND QUOTIENTS

DIFFERENCES

In subtracting one number from another, say, 5 - 3, we are seeking a number 2, which when added to 3 equals 5. In general,

the difference a - b is the number d such that b + d = a.

Example 1 a. 9 - 5 = 4 because 5 + 4 = 9.
b. 20 - 13 = 7 because 13 + 7 = 20.
c. 10 - 0 = 10 because 0 + 10 = 10.

Note that while the sum of two whole numbers a + b is always a whole number, an expression such as a - b does not always represent a whole number. For example,

2 - 5 and 5 - 8

do not represent whole numbers.

QUOTIENTS

In dividing one number by another, say, 6 -r 3, we are seeking a number 2, which when multiplied by 3 equals 6. We call 6 the dividend and 3 the divisor. We can indicate division by using the division symbol or a fraction bar.

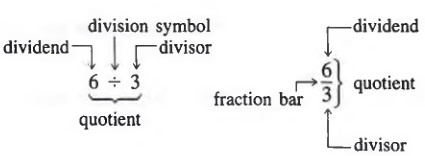
In general, the quotient is the number that, when multiplied by the divisor, gives the dividend. That is,

the quotient a ÷ b or 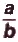is the number q, such that b · q = a.

Example 2

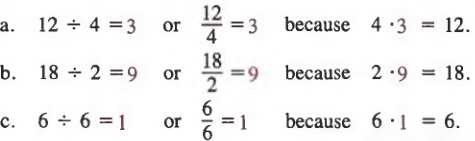
Note that while the product of two whole numbers a * b is always a whole number, an expression such as a + b or ^ does not always represent a whole number. For example,

do not represent whole numbers.

Also, notice that the commutative and associative properties do not apply to subtraction or division. That is,

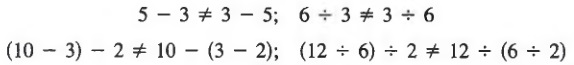
QUOTIENTS INVOLVING ZERO

In the case where the dividend is 0 and the divisor is a nonzero number, the quotient is zero. That is,

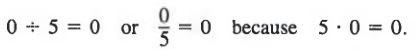
A symbol such as 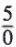is meaningless, since there is no number that, when multiplied by 0, gives 5. Nor do we use the symbol 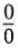to represent a number, because the product of 0 and any number is 0.

If a is any natural number,

Example 3

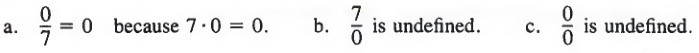
FRACTION BAR AS A GROUPING SYMBOL

If we are asked to write symbolically the phrase "divide the sum of x and y by 7," we can write

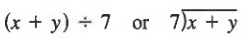
which shows that 7 is to be divided into the sum of x and y and not merely into oneor the other. In algebra, however, we prefer to show the quotient as

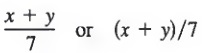
Such symbols are called fractions, where the bar beneath the x + y indicates grouping in the same way as parentheses.

When we translate a phrase such as "five subtracted from x," we must be careful to write x - 5 and not 5 - x, since the five is being taken away from x.

Example 4

EXPONENTIAL NOTATION; EQUIVALENT EXPRESSIONS

EXPONENTIAL FORM

Many times, as in the prime factors of 40 (2 * 2 * 2 * 5), the same factor occurs more than once in a product. A shorthand way of writing such product is by using exponents. An exponent is a number written to the right and a little above a factor to indicate the number of times this factor occurs in a product. The number to which an exponent is attached is called the base. The product is then referred to as a power of the factor.

In general,

Thus, 5² means (5)(5), read "five squared" or "5 to the second power";
2⁴ means (2)(2)(2)(2), read "two to the fourth power";
x³ means xxx, read "x cubed" or "x to the third power."

Example 1

We can use exponential notation when we write numbers in prime factored form.

Example 2

When we write a variable such as x with no exponent indicated, it is understood that the exponent is 1. That is,

x = x¹

In a product that involves a power as a factor, it is understood that the exponent is attached only to the base of the power and not to other factors in the product. Thus,

3x², read "three x squared," means 3xx,
5x²y³, read "five x squared y cubed," means 5xxyyy,
2x³, read "two x cubed," means 2xxx,
(2x)³, read "the quantity 2x cubed," means (2x)(2x)(2x).

Example 3

EQUIVALENT EXPRESSIONS

We say that two expressions are equivalent if they name the same number for all replacements of the variable. Although expressions may name the same number for some replacements of the variable, they are not necessarily equivalent-they must name the same number for all replacements. For example,

2x³ and (2x)³

name the same number for x = 0, but when any other value is used for x, say, x = 2, we get

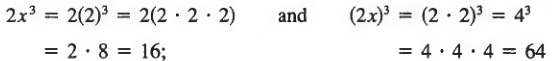
Thus, 2x³ and (2x)³ are not equivalent.

Common Errors: Note that in the expression 2x³, the exponent applies only to the factor x and not to the product 2x. In general.

abⁿ ≠ (ab)ⁿ

Also note that 23 does not mean 3 * 2. In general,

aⁿ ≠ n * a

Example 4

Use a numerical example to show that 4x² and (4x)² are not equivalent.

Solution

Let x be 2. Hence,

Thus, 4x² is not equivalent to (4x)².

ORDER OF OPERATIONS

The expression 4 + 6 · 2 can be interpreted two ways. We can see it as meaning either

(4 + 6) * 2 or 4 + (6 * 2)

in which case the result is either

10 * 2 = 20 or 4 + 12 = 16

To avoid such confusion, we make certain assumptions about parentheses and fraction bars and about the order of performing mathematical operations.

Order of Operations

1. Perform any operations inside parentheses, or above or below a fraction bar.
2. Compute all indicated powers.
3. Perform all other multiplication operations and any division operations in the order in which they occur from left to right.
4. Perform additions and subtractions in order from left to right.

Example 1 Simplify 4 + 6 · 2.

Solution

We first multiply to get

4+12

and then add to obtain

16

Expressions that involve powers require special attention, as in Examples 2-4.

Example 2 Simplify 2³ + 3(4 + 1).

Solution

First, we simplify the quantity in the parentheses

2³ + 3(5)

We then compute the power and multiply to get

8 + 15

Last, we add to obtain

23

Example 3

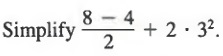
Solution

We first simplify above the fraction bar, then compute the power to obtain

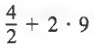
Then, we divide and multiply to get

2 + 18

And finally, we add to obtain

20

Example 4

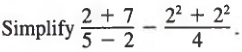
Solution

We first simplify above and below the fraction bars

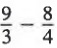
Then, we divide as indicated

3 - 2

and last, we subtract to obtain

1

NUMERICAL EVALUATION

The process of substituting given numbers for variables and simplifying the arithmetic expression according to the order of operations given in Section 1.5 is called numerical evaluation.

Example 1 If x = 3, find the value of

Solutions Substitute 3 for x and simplify.

The same process is valid when more than one variable is involved.

Example 2 If x = 2 and y = 3, find the value of a. x(y + 1) + 3
b. x³y + xy²

Solutions

Substitute 2 for x and 3 for y and simplify.

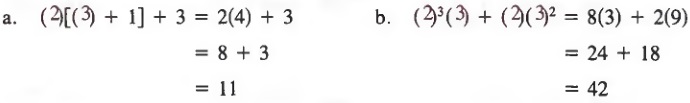
Numerical evaluation is particularly useful in working with formulas that express relationships between physical quantities.

Example 3 At an average rate r, in time t an automobile will travel a distance d given by

d = rt

If r = 50 kilometers per hour and t = 3 hours, then substituting for r and t, we get

d = (50)(3)
= 150

Thus, the distance the automobile travels is 150 kilometers.

POLYNOMIALS

TERMS

Any single collection of factors, such as

4x³, xyz, 2, or 2x²y

is called a term. If the term does not contain variables, as in

2, 10 and 7

then the term is called a constant.

POLYNOMIALS

A polynomial is the sum or difference of terms, where the exponents on the variables are natural numbers. For example,

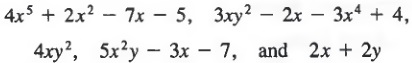
are polynomials. Notice that a polynomial can have any number of terms (poly is the Greek prefix for "many").

If a polynomial has only one term, we call it a monomial (mono is the Greek prefix for "one").

If a polynomial has exactly two terms, we call it a binomial (bi is the Greek prefix for "two").

If a polynomial has exactly three terms, we call it a trinomial (tri is the Greek prefix for "three").

Example 1

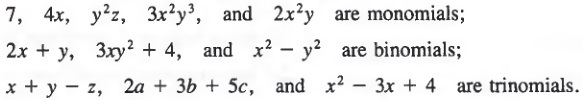
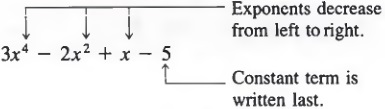
Polynomials in one variable are generally written in descending powers of the variable.

COEFFICIENTS

Any collection of factors in a term is called the coefficient of the remaining factors in the term. For example, in 3xy, 3 is the coefficient of xy, x is the coefficient of 3y, y is the coefficient of 3x, and 3x is the coefficient of y. In 3xy, the number 3 is called the numerical coefficient. In a term such as xy or x2, the numerical coefficient is understood to be 1.

Example 2

3x² has a numerical coefficient of 3;
2xy² has a numerical coefficient of 2;
x⁴ has a numerical coefficient of 1.

DEGREE OF A POLYNOMIAL

In a term containing only one variable, the exponent on the variable is called the degree of the term. The degree of a constant term is considered 0.

Example 3 3x² is of second degree;
2y³ is of third degree;
4z is of first degree (the exponent on z is understood to be 1);
1 has degree 0.

The degree of a polynomial in one variable is the degree of the term of highest degree.

Example 4

2x + 1 is of first degree;
3y² - 2y + 4 is of second degree;
y⁵ - 3y² + y is of fifth degree.

SUMS INVOLVING VARIABLES

We can add natural numbers by using a counting procedure. If we wish to add 3 to 5, we can first count out five units, then starting with the next unit, count out three more, giving us the number 8 as the sum. Now suppose we wish to add three 2's to five 2's, that is, 5(2) + 3(2). We can add these like quantities by counting five 2's, arriving at the number 10, and then counting three more 2's, to make a total of eight 2's or 16. This addition is shown on the number line in Figure 1.2

LIKE TERMS

In algebra, where terms are usually made up of both numerals and variables, we have to decide what constitutes like quantities so that we can apply the idea of addition just developed. We could add 2's as we did because they represented a common unit in each number. For variables, we are sure that x = x and ab = ab, regardless of the numbers these letters represent. It is also clear that, in general x ≠ x², a³ ≠ a², x ≠ xy, and so forth. We therefore define like terms to be any terms that are exactly alike in their variable factors. Like terms may differ only in numerical coefficients. Thus,

2x and 3x, 4x² and 7x²
5xy and 3xy, 2x²y and 4x²y

are like terms, whereas

2x and 3x²
2x²y and 2xy

are not like terms because the variable factors are different.

Note that, by the commutative property, expressions such as xy and yx are equivalent. Hence, 5yx and 3xy are like terms. Similarly, 2x2y and 4yx2 are like terms.

ADDING LIKE TERMS

In view of our definition for like terms and the discussion above, we state the following rule:

To add like terms, add their numerical coefficients

Example 1

In Example lb above, it is understood that the numerical coefficient of xy is 1.

We can illustrate the addition of like terms on a number line, by considering the unit of distance to be equal to the variable part of each term. Thus, we can represent 2x + 3x = 5x as shown in Figure 1.3.

The examples above illustrate a basic property of numbers called the distributive law:

b * a + c * a = (b + c) * a

Using the property, we can write

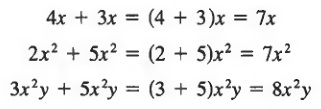
We sometimes refer to this addition process as combining like terms.

Many expressions contain both like terms and unlike terms. In such expressions we can combine only the like terms.

Example 2 Simplify.

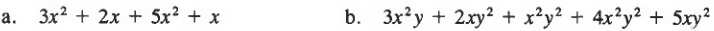
Solutions

Add the coefficients of like terms.

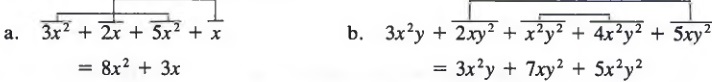
Common Errors:Notice that

2x + 3y ≠ 5xy

since 2x and 3y are not like terms, and

2x² + 3x² ≠ 5x⁴

since we add the numerical coefficients only; the exponents are not added.

DIFFERENCES INVOLVING VARIABLES

We may subtract like terms in the same way that we added like terms:

To subtract like terms, subtract their numerical coefficients.

Example 1

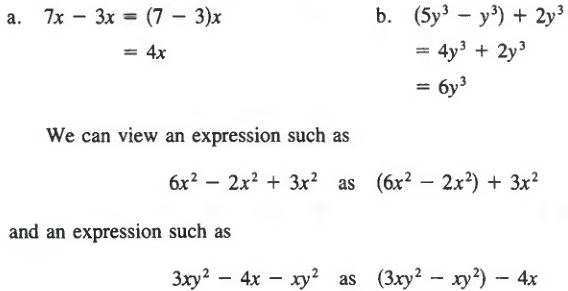
Example 2

In Example 2b above, since 2xy² and 4x are not like terms we cannot simplify further.

PRODUCTS INVOLVING VARIABLES

We have used exponents to indicate the number of times a given factor occurs in a product. For example, x³ = (x)(x)(x). Exponential notation provides us with a simple way to multiply expressions that contain powers with the same base. Consider the product (x²)(x³), which in completely factored form appears as

(x)(x) * (x)(x)(x)

This, in turn, may be written x⁵, since it contains x as a factor five times. Again, (y⁵)(y²) is equivalent to

(y)(y)(y)(y)(y) · (y)(y)

which may be written as y⁷.

By applying both the commutative and associative properties for multiplication mentioned in Section 1.2, we can arrange the factors in a product in any order we wish. For example, we can write the product (2x2y)(5xy2) in completely factored form as

(2)(x)(x)(y)(5)(x)(y)(y)

Then, by the associative and commutative laws, we can write

(2) (5) (x) (x) (x) (y) (y) (y)

which is equivalent to 10x³y³.

Example 1

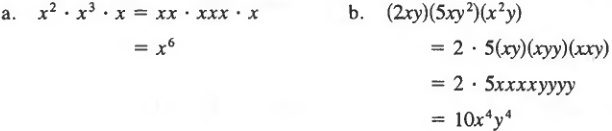
FIRST LAW OF EXPONENTS

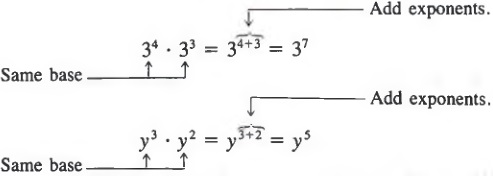
In the examples above, we can obtain the product of two expressions with the same base by adding the exponents of the powers to be multiplied. We can make a more general statement by considering the product (a^m)(aⁿ). In completely factored form, (a^m)(aⁿ) appears as

which in exponential notation is written as a^m+n. Thus,

To multiply two powers with the same base, add the exponents.

This property is called the first law of exponents. In symbols,

a^m * aⁿ = a^m+n

For example,

Example 2

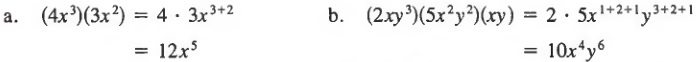
To simplify an expression involving products and sums, we follow the proper order of operations.

Example 3

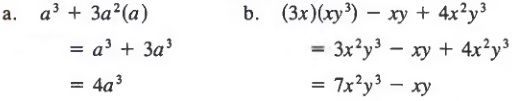
Multiply factors and then combine like terms.

Common Errors:

By the first law of exponents, we must add the exponents. Thus,

x³ * x² = x³⁺² = x⁵

QUOTIENTS INVOLVING VARIABLES

In Section 1.3 we rewrote quotients of whole numbers. In this section we will rewrite quotients involving variables, and we will assume that no divisor is equal to zero. Thus, in a quotient such as 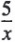, x will not represent zero.

FUNDAMENTAL PRINCIPLE OF FRACTIONS

In algebra, we can use the following fundamental principle of fractions to rewrite a quotient in which the denominator is a factor of the numerator

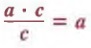
Thus, we can simplify quotients by expressing the dividend and divisor in completely factored form and dividing out common factors.

Example 1

We can also use this method for quotients involving variable factors.

Example 2

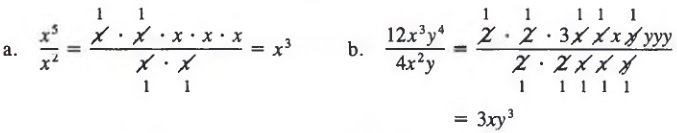
Slash bars can be used on the original quotient.

Example 3

If the exponents on the same variable in the dividend and divisor are the same, the quotient of these two powers is 1. Thus,

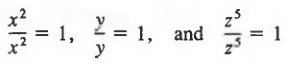
To simplify expressions involving sums, differences, products, and quotients, we follow the proper order of operations.

Example 4

Combine like terms above the fraction bar and then divide out common factors.

Common Errors: Notice that when we apply the fundamental principle of fractions, we can only divide out common factors. We cannot divide out terms. That is,

Terms cannot be divided out.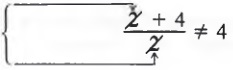

Terms cannot be divided out.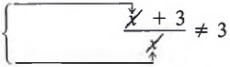

2 is not a factor of the entire numerator.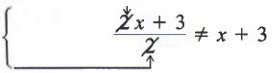

CHAPTER SUMMARY

1. The numbers 1, 2, 3, 4, ... are called natural numbers. These numbers (together with zero) are also called whole numbers. A natural number greater than 1 that is exactly divisible only by itself and 1 is called a prime number.

   A number line can be used to represent the relative order of a collection of whole numbers. The point on the number line associated with zero is called the origin.

2. Letters such as a, b, c, . . . x, y, z that are used to represent numbers are called variables.

   The following properties apply to the operations of addition and multiplication:

   Factors of a product that are prime numbers are called prime factors.

   Any meaningful collection of numbers, variables, and signs of operation is called an algebraic expression.

3. The difference a - b is the number d such that b + d = a. The quotient a ÷ b or a / b is the number q such that (b)(q) = a; the divisor b cannot equal zero. Division by zero is undefined.

4. In the power aⁿ, where aⁿ = a * a * a * * * * * a (n factors), a is called the base and n is called the exponent.
   Algebraic expressions that have identical values for all substitutions for any variables they contain are called equivalent expressions.

5. A single example can be used to show that two expressions are not equivalent. When a mathematical expression contains more than one operation, the operations must be performed in a specified order.

6. We can evaluate algebraic expressions by replacing the variables with numbers and simplifying the resulting expression.

7. A polynomial is the sum or difference of terms, where the exponents on the variables are natural numbers. Polynomials of one term, two terms, and three terms are called monomials, binomials, and trinomials, respectively. Any collection of factors in a term is called the coefficient of the remaining factors. The degree of a term containing only one variable is the exponent on the variable.

8. Terms that are exactly alike in their variable factors are called like terms. We add like terms by adding their numerical coefficients. In symbols;
   b · a + c · a = (b + c) · a Distributive law
   We subtract like terms by subtracting their numerical coefficients.

9. Products of powers with the same base can be rewritten in accordance with the first law of exponents. a^m * aⁿ = a^{m + n}

10. Quotients can be rewritten in accordance with the fundamental principle of fractions.