Integration by Partial Fractions

Partial fraction decomposition can help you with differential equations of the following form:

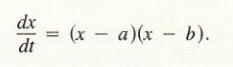
In solving this equation, we obtain

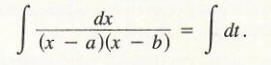
The problem is that we have no technique for evaluating the integral on the left side.A technique called integration by partial fractions, in its broadest applications, handles a variety of integrals of the form

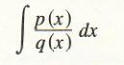
where p and q are polynomial functions. The technique of partial fractions becomes more complicated as the polynomials becomes more complicated. We shall illustrate the technique via some examples of special cases.

Example 1

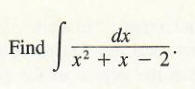
Solution Note that the denominator of the integrand can be factored:

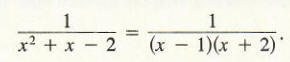
The plan is to decompose this fraction into partial fractions by finding numbers A and B for which

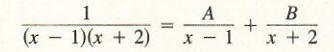
holds for all x except x = 1 and x = - 2. If this is possible, then we can integrate 1/(x^2+x-2) by finding :

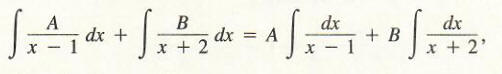
since these last two antiderivatives can be evaluated easily in terms of the natural logarithm.

We shall now show how to find A and B. Note that if we multiply both sides of the equation

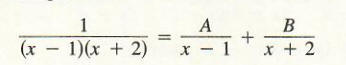
by (x - l)*(x + 2), we obtain

1 = A (x + 2) + B (x - 1).

The last equation must hold for all x, that is, it is an identity. Since it holds for all x, it must hold for any specific values of x that we choose. Observe that if we choose x = - 2, then the term involving A will become 0, and we have

l = A(-2+2)+B(-2-1)= -3B

from which we immediately get B = -1/3 . If we next choose x = 1, we have

1 = A (1+2)+B(1-1) = 3A,

and consequently A = 1/3 . Substituting these values of A and B into Formula (2), we obtain

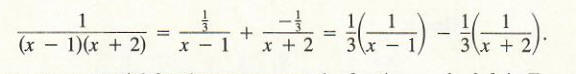
Thus, we use partial fractions to express the fraction on the left in Equation (2).

We can now complete the integration problem.

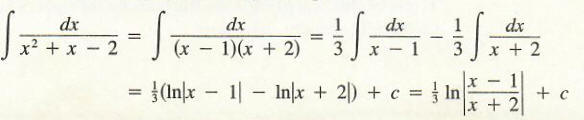
In order for the procedure used in Example 1 to work, q (x) in Equation (1) must factor into a product of linear terms, and the degree of the polynomial in the denominator q (x) must be larger than the degree of the polynomial p (x) in the numerator. If the degree of q (x) is not larger than the degree of p (x), it is necessary first to perform long division and then use the technique of Example 1.