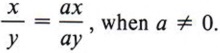Algebraic Fractions

You have encountered fractions many times since early in the study of mathematics. They occur in formulas and in many day-to-day practical problems. However, the fractions of arithmetic are made up strictly of numbers. We will now study operations on fractions whose components are algebraic expressions.

SOLVING EQUATIONS INVOLVING SIGNED NUMBERS

OBJECTIVES

Upon completing this section you should be able to:

1. Factor the numerator and denominator of a fraction.
2. Simplify algebraic fractions.

An algebraic fraction is the indicated ratio of two algebraic expressions.

In your study of arithmetic you were instructed that fractional answers were always to be left in reduced, or simplified form. For the fraction 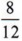you "reduced" it to by dividing the numerator and the denominator by 4. The fraction cannot be reduced because no number (other than 1) will divide both numerator and denominator. In simplifying fractions this way you were using the following definition.

A fraction is in simplified (or reduced) form if the numerator and denominator contain no common factor (other than 1).

A fraction such as is in simplified form since the numerator 2 and the denominator 3 have no common factor other than one.

To obtain the simplified form of a fraction apply the following rule.

To simplify a fraction factor the numerator and denominator completely and then divide both numerator and denominator by all common factors.

The fraction , however, is not in simplified form since numerator and denominator have a common factor of 2.

Next divide by the common factors, giving

Remember, a factor divided by itself is equal to 1.

Now divide by the common factor (x + 2) in both numerator and denominator to get

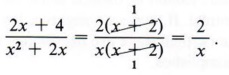
We can only divide common factors, never common terms.

In an expression such as some students are tempted to divide the 3's. Note that this is incorrect since they are terms and not factors.

Notice that even though we were able to factor the numerator and denominator, we still cannot divide since no factors are common to both. The given fraction is already in simplified form.

The fact that a given fraction might require any of the methods of factoring you have studied emphasizes again the importance of being proficient in factoring.

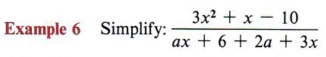
Solution Here you may use "trial and error" for the numerator and "grouping" for the denominator.

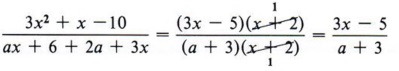
Here (x + 2) is a common factor, so both numerator and denominator may therefore be divided.

Note that the numerator 2x + 5 can be written as (2x 4- 5) * 1. Thus when the factor (2x + 5) is divided, the factor 1 remains.

Solution This type of problem requires special attention because it is a common cause for error. At first glance the factors might be mistakenly considered as common, or the fraction might be mistakenly considered as already simplified. Note that the factors cannot be divided since the signs keep them from being identical. If, however, negative 1 is factored from one of the factors, then there are like factors and division can be accomplished.

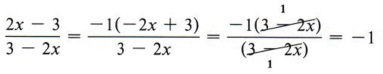
Any factors in the form of a - b and b - a are negatives of each other, thus 2x - 3 and 3 - 2x are negatives of each other.

All of these are equivalent forms of the same expression. The preferred form would be one that uses the least number of written signs. Always check your answer to see if it is equivalent to the form given in the answer section.

MULTIPLICATION OF ALGEBRAIC FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Factor numerators and denominators of all fractions being multiplied.
2. Identify and divide by all common factors.
3. Write the product in simplest form.

An algebraic fraction is the indicated ratio of two algebraic expressions.

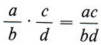is the definition of the product of two fractions. In words this says, "multiply numerator by numerator and denominator by denominator." You have used this rule many times in arithmetic as you multiplied fractions.

However, remember that all fractional answers must be in simplified form. We could follow the above definition and then simplify the answer as in the previous section. But with algebraic fractions this can lead to very difficult expressions. The following rule allows us to simplify as we multiply, so the answer will then be in simplified form.

When multiplying algebraic fractions, factor all numerators and denominators completely, then divide by all factors common to a numerator and denominator before multiplying.

The product of the remaining factors of the numerator will be the numerator of the answer and the product of the remaining factors of the denominator will be the denominator of the answer.

Again, remember common factors must be exactly alike.

We will use the dot * to indicate multiplication since using X might be confused with the variable x.

Note that (x + 2) and (2 + x) are the same but (x - 4) and (4 - x) are negatives of each other. Again, there are many possible forms for the final answers. The form given here is preferred because it contains the fewest number of signs.

There are a lot of factors in this problem. Be careful!

DIVISION OF ALGEBRAIC FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Change a division problem to a related multiplication problem.
2. Divide algebraic fractions.

Division of fractions is defined in terms of multiplication.

To divide multiply by the inverse of the divisor.

To divide one algebraic expression by another invert the divisor and change the operation to multiplication.

The divisor follows the sign. Do not invert the wrong fraction.

If no denominator is shown, it is understood to be 1.

After the problem is changed from a division problem to a multiplication problem, it is completed as in the previous section.

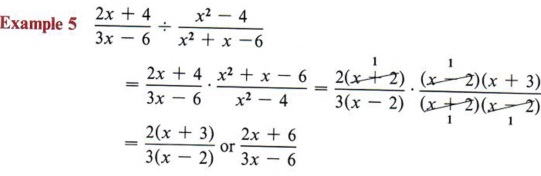
Again, note it is only the fraction following the sign that is inverted.

FINDING THE LEAST COMMON DENOMINATOR

OBJECTIVES

Upon completing this section you should be able to:

1. Factor a denominator of a fraction completely.
2. Find the least common denominator of two or more fractions.

The rule for addition and subtraction of fractions requires that the fractions to be combined must have the same denominator. As preparation for performing these operations we will now investigate the method of finding the least common denominator for any group of fractions.

A common denominator lot two or more fractions is an expression that contains all factors of the denominator of each fraction. A least common denominator contains the minimum number of factors to be a common denominator.

The least common denominator of a set of fractions is sometimes referred to as the least common multiple of the denominators.

Mental arithmetic will allow you to find the least common denominator for small numbers. If asked to add 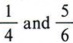, it is easy to arrive at a least common denominator of 12. If asked how we arrived at 12, we just know that 12 is the least number divisible by both 4 and 6. However, a more involved method is necessary if the numbers are larger or if the fractions are algebraic fractions.

Example 1 Find the least common denominator for

Solution This problem would require a considerable amount of guesswork, or testing possibilities, if we had no general method.

We could obtain a common denominator of these fractions by finding the product 12 X 14 X 15 X 18 = 45,360. While this number is a common denominator, it is not the least common denominator.

Let's consider the definition. From it we know that a common denominator for these numbers must contain all factors of each. In other words, we are looking for the smallest number divisible by 12, 14, 15, and 18.
First completely factor each number.

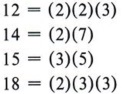
The number we are looking for must contain (2)(2)(3) in order to be divisible by 12. It must contain (2)(7) in order to be divisible by 14, and so on. Proceed as follows:
Write the factors of the first number, 12.
(2)(2)(3)
Now look at the factors of the next number, 14, and see that we need (2)(7). But since we already have a 2, we only need the factor (7). This gives
(2)(2)(3)(7).
This number is now divisible by 12 and by 14. The factors of the next number, 15, are (3) and (5). Since we already have a 3, we need only the factor 5, giving
(2)(2)(3)(7)(5).
This number is now divisible by 12, 14, and 15. The factors of the next number, 18, are (2)(3)(3). We already have 2 and one 3. Hence, we need another 3.
(2)(2)(3)(7)(5)(3) = 1,260
This number, 1,260, is a common denominator of 12, 14, 15, and 18 because it contains all factors of each and is therefore divisible by each. It is the least common denominator because it contains only those factors necessary to make it divisible by 12, 14, 15, and 18.

Note that 1,260 is considerably smaller than the number obtained by simply finding the product of all the denominators.

The preceding discussion gives rise to a rule for obtaining a least common denominator for any number of fractions, whether they be numbers or algebraic expressions.

To find the least common denominator for two or more fractions:
1. Factor each denominator completely.
2. Write the denominator of the first fraction in factored form as the proposed common denominator.
3. By inspection determine which factors of the second denominator are not already in the proposed common denominator and include them.
4. Repeat step three for each fraction.

Once mastered, this step-by-step procedure will greatly simplify your work.

Note that in finding the least common denominator we pay no attention to the numerator. This is just the denominator of the first fraction.

By inspection of the second denominator we need the additional factor (x - 2). The least common denominator is (3x - 4)(2x + l)(x - 2).

Again, the numerators have no affect on what the least common denominator will be. Sometimes the least common denominator is abbreviated as LCD.

Note that x2 is a factor in the denominator of the first fraction but not in the second fraction.

Here we have three denominators.

Solution
First denominator: 3(x + 2)
Second denominator: 2(2)(3)
Third denominator: 2(x + 3)(x + 2)
Proposed common denominator: 3(x + 2)
By inspection of the second denominator we see we need to include the factors (2) and (2). We now have 2(2)(3)(x + 2). By inspection of the third denominator we see we need the factor (x + 3). The least common denominator is 2(2)(3)(x + 2)(x + 3) or 12(x + 2)(x + 3).

EQUIVALENT FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Understand the fundamental principle of fractions.
2. Change a fraction to an equivalent fraction.

In further preparation for adding and subtracting fractions, we must be able to change a given fraction to one with a new denominator without changing the value of the original fraction.

is called the fundamental principle of fractions.

When we analyze this statement, we see two equivalent fractions and note that the numerator and denominator of have both been multiplied by the same nonzero number, a.

To change a fraction to an equivalent fraction multiply numerator and denominator by the same nonzero expression.

Why must the expression be nonzero?

You could think of this process as the reverse of reducing fractions.

Solution Since the new denominator is in factored form, by inspection we see that the original denominator (2x + 3) has been multiplied by the factor (x - 4). Therefore, the original numerator (x + 1) must also be multiplied by the factor (x - 4), giving

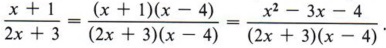
Note that in the final form of the fraction we have multiplied the factors in the numerator but have left the denominator in factored form. This is the preferred way of writing the answer.

Solution Since the original denominator (x - 3) has been multiplied by (2) and (x + 1), the original numerator (2x + 1) must also be multiplied by (2) and (x + 1).

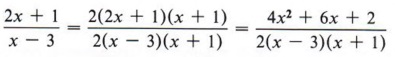
Again, note the form of the answer.

ADDITION OF ALGEBRAIC FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Add fractions having the same denominator.
2. Find the least common denominator of two or more fractions.
3. Apply the rule for adding fractions.

We are now prepared to add algebraic fractions by using the techniques discussed in the preceding two sections. You should recall the following rule from arithmetic.

The sum of two or more fractions which have the same denominator is the sum of the numerators over their common denominator.

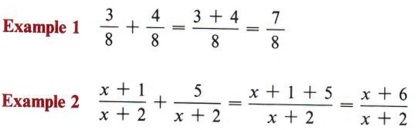
Take note that this rule only allows the sum of fractions that have the same denominator. In other words, two or more fractions can only be added if they have a common denominator. The rule for adding any two or more fractions will require the skills developed in the last two sections in addition to knowledge of combining like terms.

To add two or more fractions follow these steps:
Step 1 Find the least common denominator (LCD) for all fractions involved using the method developed in section 9-4.
Step 2 Change each fraction to an equivalent fraction having the least common denominator (section 9-5).
Step 3 Find the sum of the numerators and place this sum over the least common denominator.
Step 4 Simplify (or reduce) the fraction obtained in step 3.

These four steps should be used whenever you add fractions.

Remember to multiply the numerator as well as the denominator by the same expression.

This answer is in reduced form.

Again, don't forget to multiply the numerator by the same expression you multiply the denominator by.

Whenever the denominators have no common factors, the LCD is the product of the denominators.

Here only the first fraction must be changed in form.

The sum is

Note that the numerator 3x - 15 can be factored as 3(x - 5) and the factor (x - 5) matches a factor in the denominator.

We can use fewer written steps if we note that "common denominator" means all the fractions have the same denominator, and if all have the same denominator, then it is necessary to write the denominator only once. To illustrate this we will re-work the preceding example.

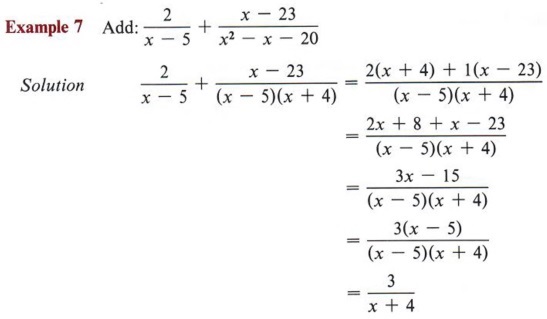
This shortcut is fine as long as you remember to multiply the numerators by the necessary factors.

Again, the denominators have no common factors so the LCD is the product of all three denominators.

SUBTRACTION OF ALGEBRAIC FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Subtract fractions having the same denominator.
2. Apply the rule for subtracting fractions with unlike denominators.

Subtraction is defined in terms of addition, so the method of subtracting algebraic fractions will be the same as adding algebraic fractions discussed in the preceding section. You will soon see why we have presented them separately.

The difference of any two fractions having the same denominator is the difference of their numerators over their common denominator.

Notice that this rule is the same as the rule for adding two fractions with the same denominator.

The steps for subtracting fractions are, therefore, the same as for adding fractions.

To subtract fractions:
Step 1 Find the least common denominator of the two fractions.
Step 2 Change each fraction to an equivalent fraction having the least common denominator.
Step 3 Find the difference of the numerators and place this result over the least common denominator.
Step 4 Simplify (or reduce) the fraction obtained in step 3.

The obvious question is, "If these two operations are the same, why study them separately?" The answer is that the subtraction gives rise to a very common error that the student must be prepared to avoid.

Notice we are subtracting the entire numerator of the second fraction. It will therefore be a good practice to place the entire numerator in parentheses with the subtraction sign in front of it.

The error referred to is often made by not recognizing that the minus sign affects the entire numerator of the second fraction and NOT just the first term.

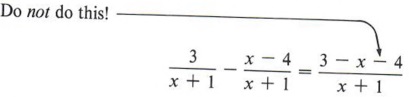
This will happen if you don't use parentheses.

The arrow points out the error most commonly made in subtraction of fractions. The best way to avoid this is to always use parentheses

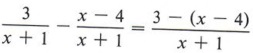
and you are not so likely to fail to change the sign properly.

Notice we placed parentheses around the numerator of the second fraction. Notice we first multiplied (x - 4) (2x - 1) and then multiplied (2x2 - 9x + 4) by -l.To multiply and change signs at the same time is to invite error.

COMPLEX FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Recognize a complex fraction.
2. Simplify a complex fraction.

Fractions are defined as the indicated quotient of two expressions. In this section we will present a method for simplifying fractions in which the numerator or denominator or both are themselves composed of fractions. Such fractions are called complex fractions.

Thus if the numerator and denominator of a complex fraction are composed of single fractions, it can be simplified by dividing the numerator by the denominator.

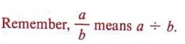
A generally more efficient method of simplifying a complex fraction involves using the fundamental principle of fractions. We multiply both numerator and denominator by the common denominator of all individual fractions in the complex fraction.

Recall that the fundamental principle of fractions states

We will use the fundamental principle to again simplify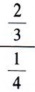

The LCD of 3 and 4 is 12. Thus

The individual fractions are

This answer could be written as the mixed number

Make sure that each term in both numerator and denominator is multiplied by the LCD.

We need the LCD of individual fractions, y is not a fraction.

EQUATIONS HAVING ALGEBRAIC FRACTIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Apply the method of solving fractional equations.
2. Determine when a fractional equation does not have a solution.

In chapter 2 we encountered equations that have fractions. However, those fractions all had numerical denominators. Now we will discuss equations that have fractions involving variables in the denominators.

The method of solving these equations will follow the same pattern as in chapter 2, but there are some additional cautions that you must be prepared to take.

You may wish to look back at some examples in chapter 3 to refresh your memory.

To refresh your memory the steps for solving such equations are repeated here.
First: Eliminate fractions by multiplying each term of the equation by the least common denominator of all fractions in the equation.
Second: Simplify by combining like terms on each side of the equation.
Third: Add or subtract the necessary quantities to get the unknown quantity on one side and the numbers of arithmetic on the other.
Fourth: Divide by the coefficient of the unknown quantity.
Fifth: Check your answer.

The main difference in solving equations with arithmetic fractions and those with algebraic fractions comes in checking. The checking process will not just be to find a possible error, but will also be to determine if the equation has an answer.

This last possibility arises because with algebraic fractions we multiply by an unknown quantity. This unknown quantity could actually be zero, which would make all the work invalid.

Remember, we may only multiply each side of an equation by a nonzero quantity.

This means that neither (x - 1) nor (x + 1) can be zero. If x = 1, then the factor (x - 1) is zero and we are in trouble!

Since division by zero is not possible, we must conclude that x = 1 is not a solution. And since we made no error in the computations we must conclude that this equation has no solution.
The correct answer is "no solution."

Checking is necessary in algebraic equations. Otherwise you could do a lot of work-make no mistake-and still miss the problems. In other words, x = 1 is not a solution since it gives a statement with no meaning.

Remember, the check is an extremely important step as it will determine whether there is a solution or not.

Notice in these examples that when we have x2 terms, they cancel out and we are left with a linear equation. If they did not cancel out, we would have an x2 term in the equation. This type of equation (quadratic) will be dealt with in chapter 11.

Thus, x = -5 is a solution.

Therefore, 11 is the amount by which the numerator was increased.

SUMMARY

Key Words

• An algebraic fraction is the indicated ratio of two algebraic expressions.
• A fraction is in simplified form if the numerator and denominator have no common factor other than 1.
• A common denominator for two or more fractions is an expression that contains all factors of the denominators of each fraction.
• A least common denominator contains the minimum number of factors to be a common denominator.
• The fundamental principle of fractions is
  
• Complex fractions are those in which the numerator or denominator (or both) contains a fraction.

Procedures

• To simplify or reduce fractions to lowest terms factor the numerator and denominator and divide by all like factors.
• To multiply fractions factor all numerators and denominators and divide by all like factors before multiplying.
• To divide by a fraction invert the divisor and then multiply.
• To find a least common denominator (LCD) first factor all denominators, then find a denominator that contains all factors of each denominator but does not contain any unnecessary factors.
• To change a fraction to an equivalent fraction multiply numerator and denominator by the same nonzero expression.
• To add fractions follow these steps:
  1. Find the least common denominator.
  2. Change each fraction to an equivalent fraction having the LCD as its denominator.
  3. Add the numerators and place over the LCD.
  4. Simplify or reduce the answer.
• To subtract fractions proceed as in addition but combine the numerators by subtracting.
• Complex fractions may be simplified by multiplying numerator and denominator of the complex fraction by the LCD of all fractions in the expression.
• To solve equations having fractions first eliminate all fractions by multiplying the entire equation by the LCD of the fractions involved. The resulting equation is then solved, and the solution must be checked in the original equation.