Inequalities
The inequalities section of QuickMath allows you to solve virtually any inequality or system of inequalities in a single variable. In most cases, you can find exact solutions. Even when this is not possible, QuickMath may be able to give you approximate solutions to almost any level of accuracy you require. In addition, you can plot the regions satisfied by one or more inequalities in two variables, seeing clearly where the intersections of those regions occur.
What are inequalities?
Inequalities consist of two or more algebraic expressions joined by inequality symbols. The inequality symbols are :| < | less than |
| > | greater than |
| <= | less than or equal to |
| >= | greater than or equal to |
| != or <> | not equal to |
Here are a few examples of inequalities :
|
Solve
The Solve command can be used to solve either a single inequality for a single unknown from the basic solve page or to simultaneously solve a system of many inequalities in a single unknown from the advanced solve page. The advanced command allows you to specify whether you want approximate numerical answers as well as exact ones, and how many digits of accuracy (up to 16) you require.
Multiple inequalities in the advanced section are taken to be joined by AND. For example, the inequalities
2 x - 1 > 0x^2 - 5 < 0
on two separate lines in the advanced section are read by QuickMath as
2 x - 1 > 0 AND x^2 - 5 < 0In other words, QuickMath will try to find solutions satisfying both inequalities at once.
Plot
The Plot command, from the Graphs section, will plot any inequality involving two variables. In order to plot the region satisfied by a single inequality involving x and y, go to the basic inequality plotting page, where you can enter the inequality and specify the upper and lower limits on x and y that you want the graph to be plotted for. The advanced inequality plotting page allows you to plot the union or intersection of up to 8 regions on the one graph. You have control over such things as whether or not to show the axes, where the axes should be located and what the aspect ratio of the plot should be. In addition, you have the option of showing each individual region on its own.
Introduction to Inequalities
An equation says that two expressions are equal, while an inequality says
that one expression is greater than, greater than or equal to, less than, or
less than or equal to, another. As with equations, a value of the variable for
which the inequality is true is a solution of the inequality, and the set of all
such solutions is the solution set of the inequality. Two inequalities with the
same solution set are equivalent inequalities. Inequalities are solved with the
following properties of inequality.
PROPERTIES OF INEQUALITY
For real numbers a, b, and c:
(a)
(The same number may be added to both sides of an inequality without changing the solution set.)
(b) 
(Both sides of an inequality may be multiplied by the same positive number without changing the solution set.)
(c)
(Both sides of an inequality may be multiplied by the same negative number
without changing the solution set, as long as the direction of the inequality
symbol is reversed.)
Replacing < with >, results in equivalent properties.
NOTE Because division is defined in terms of multiplication, the word
"multiplied" may be replaced by "divided" in parts (b) and (c) of the properties
of inequality.
Pay careful attention to part (c): if both sides of an inequality are multiplied by a negative number, the direction of the inequality symbol must be reversed. For example, starting with the true statement - 3 < 5 and multiplying both sides by the positive number 2 gives
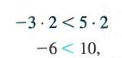
still a true statement. On the other hand, starting with - 3 < 5 and
multiplying both sides by the negative number -2 gives a true result only if the
direction of the inequality symbol is reversed.
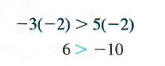
A similar situation exists when dividing both sides by a negative number. In
summary, the following statement can be made.
When multiplying or dividing both sides of an inequality by a negative
number, we must reverse the direction of the inequality symbol to obtain an
equivalent inequality.
LINEAR INEQUALITIES A linear inequality is defined in a way similar to a
linear equation.
A linear inequality in one variable is an inequality that can be written in the
form

where a <> 0.
Example 1
Solve the inequality -3x + 5 > -7.
Use the properties of inequality. Adding - 5 on both sides gives
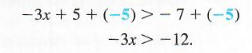
Now multiply both sides by -1/3. (We could also divide by -3.) Since -1/3 < 0, reverse the direction of the inequality symbol.
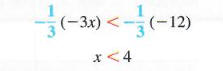
The original inequality is satisfied by any real number less than 4. The solution set can be written {x|x < 4}. A graph of the solution set is shown in Figure 2.6, where the parenthesis is used to show that 4 itself does not belong to the solution set.
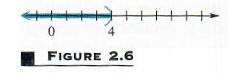
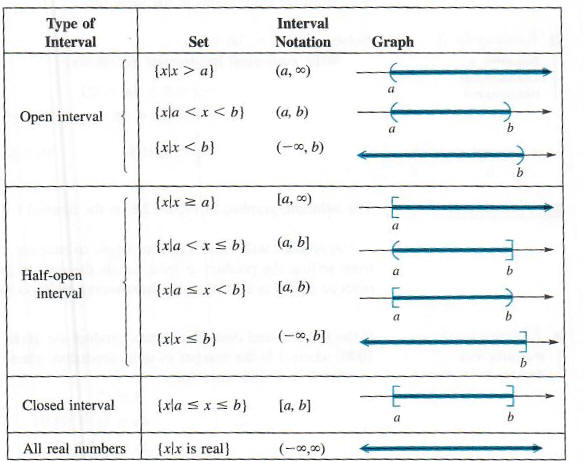
The set {x|x < 4}, the solution set for the inequality in Example 1, is an example
of an interval. A simplified notation, called interval notation, is used for
writing intervals. With this notation, the interval in Example 1 can be written
as (-oo, 4). The symbol -oo is not a real number; it is used to show that the
interval includes all real numbers less than 4. The interval (-oo, 4) is an example of an
open interval, since the endpoint, 4, is not part of the interval. Examples of
other sets written in interval notation are shown below. A square bracket is
used to show that a number is part of the graph, and a parenthesis is used to
indicate that a number is not part of the graph. Whenever two real numbers a and
b are used to write an interval in the chart that follows, it is assumed that a
< b.
Example 2
Solve 4 - 3y < 7 + 2y. Write the solution in interval notation and graph
the solution on a number line. Write the following series of equivalent
inequalities.

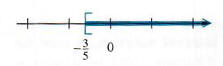
In set-builder notation, the solution set is {y|y>=3/5}, while in interval
notation the solution set is (-3/5, oo). See Figure 2.7 for the graph of the solution set.
From now on, the solutions of all inequalities will be written with interval
notation.
THREE-PART INEQUALITIES The inequality -2 < 5 + 3m < 20 in the next
example says that 5 + 3m is between -2 and 20. This inequality can be solved
using an extension of the properties of inequality given above, working with all
three expressions at the same time.
Solve -2 < 5 + 3m < 20.
Write equivalent inequalities as follows.
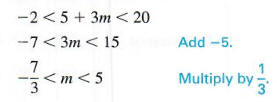
The solution is graphed in Figure 2.8

QUADRATIC INEQUALITIES The solution of quadratic inequalities depends on
the solution of quadratic equations.
A quadratic inequality is an inequality that can be written in the form

We will discuss quadratic inequalities in the next section.