Variables
Using equations and inequalitie to solve word problems
In chapter 2 we developed the techniques for solving equations. Equations arise as a means of solving verbal or word problems. Since word problems are a large part of algebra, it is necessary to develop techniques of solving them. In this chapter we will concentrate on ways of outlining and solving verbal problems.
FROM WORDS TO ALGEBRA
OBJECTIVES
Upon completing this section you should be able to:
- Change a word phrase to an algebraic expression.
- Express a relationship between two or more unknowns in a given statement by using one unknown.
The primary task when attempting to solve a word problem is one of translation. The problem is written in one language and must be translated into another- the language of algebra. This translation process must be precise if we are to be successful in solving the problem.
Example 1 Statement: A number increased by seven is twelve.
Algebraic translation: x + 7 = 12
Do these two statements have the same meaning? Does the algebraic equation make the same statement as the English sentence? If so, we have correctly translated from one language to another and can easily solve for the missing number.
Before we begin to outline completed sentences or solve problems we need to review the meaning of certain phrases.
Example 2 Write an algebraic expression for: A certain number decreased by four.
Solution
If we let x represent "a certain number," and recognize that "decreased by" is subtraction, then our answer is x - 4.
| Note that a phrase will yield only an algebraic expression and not a complete equation. It is impossible to solve for the unknown without a complete equation. |
| There are key words that give clues to the operations to be used. Addition-words such as "increased by," "sum," "more than," "greater than," "total." Subtraction-words such as "decreased by," "less than," "difference," "diminished by." Multiplication-words such as "times," "of," "product," "twice." Division-words such as "quotient," "divided by." |
Example 3 Write an algebraic expression for: Five times a certain number.
Solution
If x represents "a certain number," then the expression would be 5x.
Example 4 Write an algebraic expression for: Five more than a certain numoer.
Solution
If x represents "a certain number," then "more than" means addition, the expression is x + 5.
Example 5 Write an algebraic expression for: Seven more than twice a certain number.
Solution
Again, allowing x to represent the unknown number, we have 2x + 7.
Example 6 Write an algebraic expression for: 5% of a given number.
Solution
First write 5% as the decimal .05. If x represents the "given number," then the expression would be .05x .
Example 7 Write an algebraic expression for: The value in cents of d dimes.
Solution
The value of a dime is 10 cents. Therefore to indicate the value of d dimes multiply 10 by d, obtaining 10d.
| It may not always be possible to relate the unknowns in a problem using only one unknown. You will be able to do so, however, with all problems in this chapter. |
When more than one unknown number is involved in a problem, we try to outline it in such a way that all unknowns are expressed in terms of one unknown.
Example 8 The Sears Tower in Chicago is eight stories taller than the Empire State Building in New York. Write algebraic expressions for the height of each building using one unknown.
Solution
From the information given we do not know how many stories either building has. We will choose one of the buildings and represent the number of stories by x.
Let x = number of stories in the Empire State Building.
Then x + 8 = number of stories in the Sears Tower.
| It may not always be possible to relate the unknowns in a problem using only one unknown. You will be able to do so, however, with all problems in this chapter. |
We could also choose x to represent the height of the Sears Tower. Then x - 8 would represent the height of the Empire State Building.
Example 9 The length of a rectangle is three meters more than the width. Write expressions for the length and width using one unknown.
Solution
Let x = width of the rectangle.
Then x + 3 = length of the rectangle.
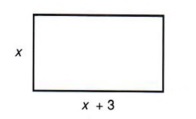
| It is sometimes helpful to use a diagram to see the relationships between unknowns. |
Example 10 The width of a rectangle is one-fourth the length. Write expressions for the length and width using one unknown.
Solution
Let x = width.
Then 4x = length.
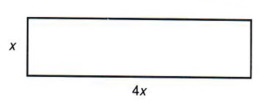
Note that if we were to let x represent the length, we would have a fraction representing the width. This certainly would not be wrong but we can avoid the use of fractions by careful selection.

Example 11 The sum of two numbers is 20. Write expressions for both numbers using one unknown.
Solution
Let x = first number.
Then 20 - x = second number.
| We could also let x = second number. What expression would represent the first number? |
Example 12 Express algebraically the relationship of the unknown in this sentence: A certain number is four more than a second number and is three less than a third number.
Solution
To express these three numbers algebraically first decide which will be represented by x.
For instance, if x represents the first number, we have the following:

Ask yourself, "Is the first number four more than the second?" and "Is the first number three less than the third?" If the answers are "yes," you have correctly outlined the sentence.
| Which number to represent by x is arbitrary, but re-read the relationships several times to see if one option is preferable over another. |
Now suppose, in the same example, we decide to allow x to represent the second number.
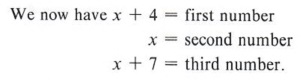
Ask the same questions again, "Is the first number four more than the second?" and "Is the first number three less than the third?" This outline is also correct.
| Represent the three numbers if x represents the third number. |
SOLVING WORD PROBLEMS
OBJECTIVES
Upon completing this section you should be able to:
- Correctly translate a word problem to an algebraic equation.
- Solve the equation and find the solution to the problem.
In the preceding exercises we outlined relationships between unknowns within a statement. If we are to solve a problem and find the unknown numbers, there must be within the problem a sentence that yields an equation.
Example 1 The Sears Tower in Chicago is eight stories taller than the Empire State Building in New York. If the total number of stories in both buildings is 212, find the number of stories in each building.
Solution
From example 8 in the previous section we have
x = number of stories in the Empire State Building
x + 8 = number of stories in the Sears Tower.
This time, however, we have the added statement that the total number of stories is 212.
| The word "total" implies addition. |
Thus, we can write the equation
x + (x + 8) = 212.
Solving this equation gives
2x = 204
x = 102.
| What does x represent? |
Notice that we have found only the number of stories in the Empire State Building. The question asked us to find the number of stories in each building. Thus, to find the number of stories in the Sears Tower we must substitute 102 for x in the expression x + 8, obtaining
x + 8 = (102) + 8 = 110.
The answers are
- number of stories in the Empire State Building = 102
- number of stories in the Sears Tower =110.
| Always re-read the problem to make sure you have answered the question. Get in the habit of always summarizing your answers. Checking your answers is one of the most important parts of the solution. |
To check the answers, 110 is eight more than 102 and the sum of 110 and 102 is 212.
Example 2 The length of a rectangle is three meters more than the width. Find the length and width if the perimeter of the rectangle is 26 meters.
Solution
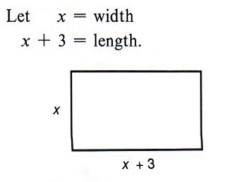
Since the perimeter is equal to the sum of twice the length and twice the width, or P = 2l + 2w, we can write the equation
2(x) + 2(x + 3) = 26.
Solving, we obtain
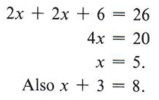
Thus, the width is 5 meters and the length is 8 meters.
Check: The length (8) is three more than the width (5), and the perimeter is 2(8) + 2(5) = 16 + 10 = 26.
|
The perimeter is the distance around the figure. Thus, two sides of the rectangle measure x and the other two sides measure x + 3. Again, the check is very important. |
Example 3 he width of a rectangle is one-fourth the length. If the perimeter is 200 centimeters, find the length.
Solution
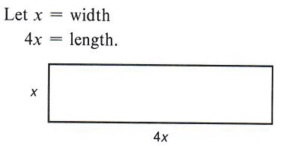
Again, the perimeter is twice the width plus twice the length. Therefore,
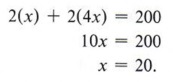
The problem asks lor the length only. Thus, 4x = 4(20) = 80. The length is 80 cm.
Check: The width (20) is one fourth the length (80). Also, the perimeter is 2(20) + 2(80) = 40 + 160 = 200.
|
This particular way of stating the unknowns avoids fractions. What does x represent? Try this problem again using x = length, x/4 = width. Which way is easier? |
Example 4 The sum of two numbers is 20. Their difference is 4. Find the numbers.
Solution

If the difference of the two numbers is 4, write the equation x - (20 - x) = 4.
Solving, we obtain
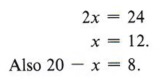
The two numbers are 8 and 12.
Check: The sum of 8 and 12 is 20. The difference of 8 and 12 is 4.
| We could also write the equation (20 - x) - x = 4 since we don't know which number is larger. Solve the above equation. |
Example 5 A certain number is four more than a second number and three less than a third number. Find the number if their sum is 23.
Solution
In this problem we are asked to find the numbers and are given a statement about their sum.
If we let x represent the first number, we have

The statement "their sum is 23" gives the equation
x + (x - 4) + (x + 3) = 23.
If we now solve the equation, we obtain
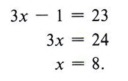
Leaving the answer as x = 8 would not be a solution to the problem. We are asked to "find the numbers." The answer must be

We check the problem by noting that the first number (8) is four more than the second (4) and is three less than the third (11) and that their sum is 23.
| Again, we could just as well let x represent the second or third number. The important thing to remember is to label each algebraic expression with the number that it represents. |
| Do not just solve the equation for x and think you have solved the problem. Check to see what x represents and reread the problem to see what it is asking for. |
We have followed five basic steps in solving the above examples. These steps should be observed when solving any word problem.
- Write expressions for the unknowns.
- Write an equation that relates the unknowns to each other.
- Solve the equation.
- Make sure you have answered the question.
- Check your answers to make sure they agree with the original problem.
| Make sure you know these five important steps before working the exercise sets. |