Example: 2x-1=y,2y+3=x
To see your tutorial, please scroll down
Definitions, properties and solution of linear inequalities in one variable
Definitions and Notation
When the real numbers a and b are represented by points on a number line, one of the following relationships hold:
1. When the graph of a lies to the right of the graph of b, then a is greater than b, denoted by a>b.
2. When a and b represent the same point, then a equals b, denoted by a = b.
3. When the graph of a lies to the left of the graph of b, then a is less than b, denote by a < b.
Note that the statements a > b and b < a are equivalent.
Examples 1. 5 lies to the right of 2, 5 > 2.
2. -8 lies to the left of -6,-8<-6.
The statement 10 > 4 means that if we subtract 4 from 10, we get a positive number, 10-4 = +6
The statement -3 > -8 means that if we subtract -8 from -3, we get a positive number, (-3)-(-8) = -3+8 = +5
Definition For a,b∈R, a>b means that a-bis a positive number.
If a-b is a positive number, we can write
a-b = k where a,b,k∈R, k>0
Since a-b = k and a= b+k are equivalent statements,
a>b means a = b+k, where k>0
If ais grater than or equal to b, the notation a>=b is used. Thus a>=b means either a>bor a=b.
If ais less than or equal to b, the notation a<=b is used. Thus a<=b means either a>=b or a=b.
Definition The relation >,<,≥,≤ are called order relations.
To represent 
graphically. draw a ray from the point whose coordinate is --3 in the positive direction. Place a hollow circle at the point to denote that the point is not included on the ray (Figure 5.1).
Figure 5.1
To represent 
graphically, draw a ray from the point whose coordinate is 5 in the negative direction. Place a hollow circle at the point to denote than the point is not included on the ray (Figure 5.2).
Figure 5.2
To represent 
graphically. draw a ray from the point whose coordinate is 2 in the positive direction. Place a solid dot at the point to denote that the point is included on the ray (Figure 5,3).
Figure 5.3
To represent 
graphically, draw a ray from the point whose coordinate is -1 in the negative direction. Place u solid dot at the point to denote that the point is included on the ray (Figure 5.4),
Figure 5.4
Properties of the Order Relations
Since a > b and b < a are equivalent statements. from the theorems below for the “greater than” relation we can derive similar theorems for the “less than" relation.
THEOREM 1
Let a,b,c∈R; if a>b, then a>c.
EXAMPLES 1. -2 > -10 and -10 > -20;
hence -2 > -20
2. -1 < 7 and 7 < 13;
hence -1 < 13
THEOREM 2
Let a,b,c,d∈R if a>b and c>d, then a+c>b+d
EXAMPLES 1. 5>2 and -8>-20
5+(-8)=-3 and 2+(-20)=-18
Since -3>-18, then 5+(-8)>2+(-20)
2. -2<0 and 10<14
-2+10 = 8 and 0+14 = 14
Since 8<14, then -2+10<0+4
THEOREM 3
Let a,b,c∈R; if a>b, then a+c>b+c
EXAMPLES 1. 20>7
20+(-30) = -10 and 7+(-30) = -23
Since -10>-23, then 20+(-30)>7+(-30.
2. -10<-2
-10+5 = -5 and -2+5 = 3
Since -5<3, then -10+5<-2+5.
THEOREM 4
Let a,b,c,d∈R, and a,b,c,d>0;
if a>band a>d, then ac>bd
EXAMPLES 1. 7>3 and 8>2
7(8) = 56 and 3(2) = 6
Since 56>6, then 7(8)>3(2).
2. 4<9 and 5<7
4(5) = 20 and 9(7) = 63
Since 20<63, then 4(5)<9(7).
THEOREM 5
Let a,b,c∈R, c>0; if a>b, then ac>bc
EXAMPLES 1. 5>-2 and 3>0
5(3) = 15 and -2(3) = -6
Since 15>-6, then 5(3)>-2(3).
2. -8<-3 and 5>0
-8(5) = -40 and -3(5) = -15
Since -40<-15, then -8(5)<-3(5).
THEOREM 6
Let a,b,c∈R,c>0; if a>b, then ac>bc.
EXAMPLES 1. 15>12 and -2<0
15(-2) = -30 and 12(-2) = -24
Since -30<-40, then 15(-2)<12(-2).
2. -10<3 and -4<0
-10(-4) = 40 and 3(-4) = -12
Since 40>-12, then -10(-4)>3(-4)
Note
if a,b∈R and a>b, then -a<-b
20>6 hence -20<-6
15>-4 hence -15<4
Solution of Linear Inequalities in One Variable
The following are examples of statements of order of two algebraic expressions
1. 5x<5x+2
2. x^2+y^2>=0
3. 7x+2<3x+18
4. 2x+9>=x+20
5. 3x+7<=3(x+1)
6. 6(x+y)>6x+6y+1
Statements 1 and 2 are true for all real values of the variables involved. Such statements are called absolute statements.
Statements 3 and 4 are true for some but not all real values of the variable involved. Statement 3 is true when x is less than -5. Statement 4 is true when x is greater than or equal to 11. Such statements are called conditional inequalities or. simply.
inequalities.
Statements 5 and 6 are not true for any real number.
The set of all numbers that satisfy the inequality is called the solution set of the inequality.
Note A linear equation in one variable has one element in its solution set. The solution set the equation 3x- 4 = 5 is {3}.
A linear inequality in one variable has more than one element in its solution set. The solution set of the inequality 3x-4>5 is 
, that is, all the real numbers that are greater than 3.
DEFINITION Two inequalities arc said to be equivalent if they have the same solution set.
To find the solution set of an inequality, we must first state some theorems.
THEOREM 1 If P.Q. and Tare polynomials in the same. variable and P > Q is an inequality then P > Q and P + T > Q + T are equivalent.
Theorem 1 shows that we can add a polynomial to both sides of the inequality and obtain an equivalent inequality.
EXAMPLE: 1. If x+7>15
then x+7+(-7)>15+(-7)
x>8
x > 8 is equivalent to x+7>15
To find the solution set of a linear inequality in one variable, apply the previous theorem to obtain an equivalent inequality of the form
Note When both sides of the inequality contain terms that have the variable as at factor and terms that do not have the variable as a factor. form an equivalent inequality that has at the terms with the variable as a factor on one side and the terms not having the variable on the other side. This can be accomplished by adding the additive inverses (negatives) of the terms to both sides of the inequality.
EXAMPLES Find the solution set of the inequality
x+5>2
Solution
Adding -5 to both sides of the inequality, we get:
x-5-5>2-5
x>-3
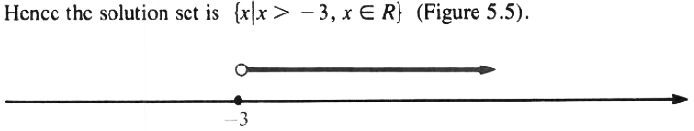
FIGURE 5.5
EXAMPLES
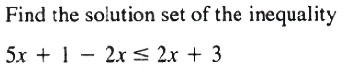
Solution
FIGURE 5.6
Note When the inequality involves symbols of grouping. first perform the operations that these symbols designate.
EXAMPLES Find the solution set of the inequality
Solution
EXAMPLES Find the solution set of the inequality
Solution
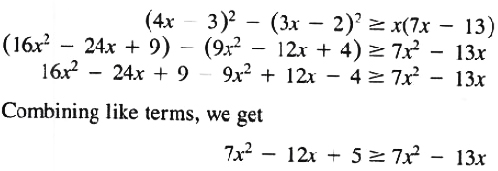
Adding (-5-7x^2+13x)
to both sides of inequality,
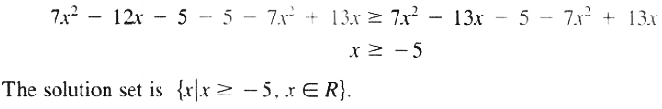
EXAMPLES List the elements in the set
Solution Consider the statement
2(x-5)+7<8-(3-2x)
2x-10+7<8-3+2x
2x-2x<8-3+10-7
0x<8
Since 0x<8
is true for all real values of x, we have
EXAMPLES List the elements in the set
Solution Consider the statement
5-3(2-x)>4-3(1-x)
5-6+3x>4-3+3x
3x-3x>4-3-5+6
0x>2
Since 0x>2 in not true for any real value of x we have
THEOREM 2
Theorem 2 shows that if we multiply both sides of an inequality by a positive real number, we obtain an equivalent inequality.
EXAMPLES 1. 2x>6
1/2(2x)>1/2(6), that is, x>3
x>3 is equivalent to 2x>6
2. 3/4(x)<-9
4/3(3/4X)<4/3(-9), that is, x<-12
x<-12 and 3/4x<-9 are equivalent.
EXAMPLE Find the solution set of the inequality
Solution
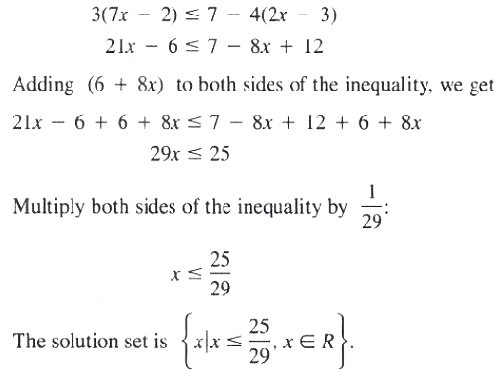
EXAMPLE Find the solution set of the inequality
3/2x+1/6>2/3x-2/3
Solution Multiply both sides of the inequality by the least common denominator, which is
9x+1>4x-4
Adding (-1-4x) to both sides, we get
5x>-5
Multiply both sides of the inequality by 1/5
x>-1
THEOREM 3
Theorem 3 shows that if we multiply both sides of an inequality by a negative number, an equivalent inequality results with the direction of the order relation reversed.
EXAMPLES 1. -5x>10
-(1/5)(-5x)<-(1/5)(10) that is x<-2
x<-2 and -5x<-10 are equivalent
2. -4x<-5
-(1/4)(-4x)>-(1/4)(-8), that is x>2
x>2 and -4x<-8 are equivalent
EXAMPLE Find the solution set of the inequality
Solution
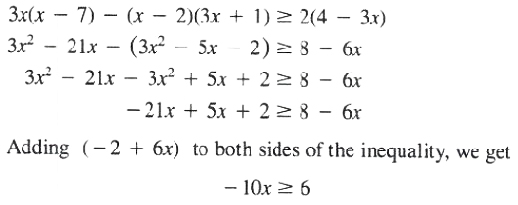
Multiply both sides of the inequality by -1/10 and reverse the direction of the order relation:
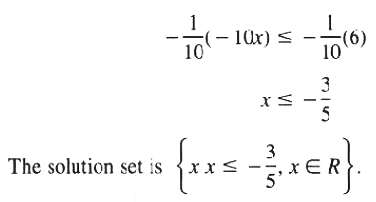
EXAMPLE Find the solution set of the inequality
(4x+5)(3x-2)-4(x+1)(3x-1)<-6
Solution (4x+5)(3x-2)-4(x+1)(3x-1)<-6
12x^2+7x-10-12x^2-8x+4<-6
-x-6<-6
Add (+6) both sides; -x<0
Multiply both sides of the inequality by (-1) and reverse direction of the order relation:
x>0
