Basics of complex number
COMPLEX NUMBERS
In the next section we will solve quadratic equations, which have a term raised to the second power (for example, x^2- 4x + 3 = 0). Solutions of quadratic equations may not be real numbers. For example, there are no real number solutions to the quadratic equation
x^2+1=0.
A set of numbers is needed that permits the solution of all quadratic equations. To get such a set of numbers, the number i is defined as follows.
DEFINITION OF i i^2=-1 or i=root(-1)
Numbers of the form a + bi, where a and b are real numbers, are called complex numbers. Each real number is a complex number, since a real number a may be thought of as the complex number a + 0i. A complex number of the form a + bi, where b is nonzero, is called an imaginary number. Both the set of real numbers and the set of imaginary numbers are subsets of the set of complex numbers. (See Figure 2.3. which is an extension of Figure 1.5 in Section 1.1.) A complex number that is written in the form a + bi or a + ib is in standard form. (The form a + ib is used to simplify certain symbols such as iroot(5), since root(5)i could be too easily mistaken for root(5i))
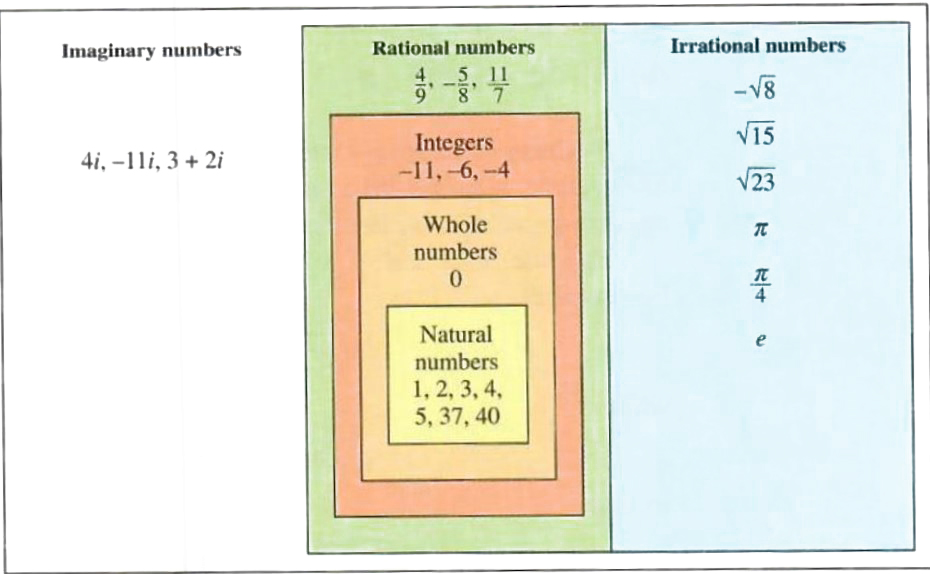
FIGURE 2.3 Complex numbers (Real numbers are shaded.)
Example 1.
IDENTIFYING KINDS OF COMPLEX NUMBERS
The following statements identify different kinds of complex numbers
(a) -8,root(7), and PIare real numbers and complex numbers.
(b) 3i,-11i,iroot(14), and 5+i are imaginary numbers and complex numbers.
Example 2.
WRITING COMPLEX NUMBERS IN STANDARD FORM
The list below shows several numbers, along with the standard form of each number.
| Number | Standard Form |
| 6i | 0+6i |
| 9 | -9+0i |
| 0 | 0+0i |
| -i+2 | 2-i |
| 8+iroot(3) | 8+iroot(3) |
Many of the solutions to quadratic equations in the next section will involve expressions such as root(-a), for a positive real number a, defined as follows.
DEFINITION OF root(-a) If a>0, then
root(-a)=iroot(a)
Example 3.
WRITING root(-a) AS iroot(a)
Write each expression as the product of i and a real number.
(a) root(-16)=iroot(16)=4i
(b) root(-70)=iroot(70)
Products or quotients with negative radicands are simplified by first rewriting root(-a) as iroot(a) for positive numbers a. Then the properties of real numbers can be applied, together with the fact that i^2=-1.
The rule root(c)*root(d)=root(cd) is valid only when c and d are not both negative. For example,
root((-4)(-9))=root(36)=6,
While
root(-4)*root(-9)=2i(3i)=6i^2=-6,
so that
root((-4)(-9)) is not equal to root(-4)*root(-9).
CAUTION When working with negative radicands, be sure to use the definition root(-a)=iroot(a) before using any of the other rules for radicals.
Example 4.
FINDING PRODUCTS AND QUOTIENTS INVOLVING NEGATIVE RADICANDS
Multiply or divide as indicated.
(a) root(-7)*root(-7)=iroot(7)*iroot(7)
=i^2*(root(7))^2
=(-1)*7 i^2=-1
=-7
(b) root(-6)*root(-10)=iroot(6)*iroot(10)
=i^2*root(60)
=-1*2root(15)
=-2root(15)
(c) (root(-20))/(root(-2))=((i)root(20))/((i)root(2))=root(20/2)=root(10)
(d) (root(-48))/(root(24))=((i)root(20))/(root(24))=(i)root(2)
OPERATIONS ON COMPLEX NUMBERS Complex numbers may be added, subtracted, multiplied, and divided using the properties of real numbers, as shown by the following definitions and examples.
The sum of two complex numbers a + bi and c + di is defined as follows.
ADDITION OF COMPLEX NUMBERS
(a+bi)+(c+di)=(a+c)+(b+d)i
Example 5.
ADDING COMPLEX NUMBERS
Find each sum.
(a) (3-4i)+(-2+6i)
=[3+(-2)]+[-4+6]i
=1+2i
(b) (-9+7i)+(3-15i)
=-6-8i
Since (a + bi) + (0 + 0i) = a + bi for all complex numbers a + bi, the number 0 + 0i is called the additive identity for complex numbers. The sum of a + bi and -a-bi is 0 + 0i, so the number -a-bi is called the negative or additive inverse of a + bi.
Using this definition of additive inverse, subtraction of complex numbers a + biand c + di is defined as
(a+bi)-(c+di)
=(a+bi)+(-c-di)
=(a-c)+(b-d)i
SUBTRACTION OF COMPLEX NUMBERS
(a+bi)-(c+di)=(a-c)+(b-d)i
Example 6.
SUBTRACTING COMPLEX NUMBERS
Subtract as indicated.
(a) (-4+3i)-(6-7i)
=(-4-6)+[3-(-7)]i
=-10+10i
(b) (12-5i)-(8-3i)
=(12-8)+(-5+3)i
=4-2i
The product of two complex numbers can be found by multiplying as if the numbers were binomials and using the fact that i^2=-1, as follows.
(a+bi)(c+di)
=ac+adi+bic+bidi
=ac+adi+bci+bdi^2
=ac+(ad+bc)i+bd(-1)
(a+bi)(c+di)=(ac-bd)+(ad+bc)i
Based on this result, the product of the complex numbers a + bi and c + di is defined in the following way.
MULTIPLICATION OF COMPLEX NUMBERS
(a+bi)(c+di)=(ac-bd)+(ad+bc)i
This definition is not practical to use. To find a given product, it is easier just to multiply as with binomials.
Example 7.
MULTIPLYING COMPLEX NUMBERS
Find each of the following products
(a) (2-3i)(3+4i)
=2(3)+2(4i)-3i(3)-3i(4i)
=6+8i-9i-12i^2
=6-i-12(-1) i^2=-1
=18-i
(b) (5-4i)(7-2i)
=5(7)+5(-2i)-4i(7)-4i(-2i)
=35-10i-28i+8i^2
=35-38i+8(-1)
=27-38i
(c) (6+5i)(6-5i)
=6^2-25i^2 Product of the sum and difference of two terms
=36-25(-1) i^2=-1
=36+25
=61 or 61+0i Standard form
(d) (4+3i)^2
=4^2+2(4)(3i)+(3i)^2 Square of a binomial
=16+24i+(-9)
=7+24i
Powers of i can be simplified using the facts that i^2=-1 and 1^4=1. The next example shows how this is done.
Example 8.
SIMPLIFYING POWERS OF i.
(a) i^15
Since i^2=-1the value of a power of i is found by writing the given power as a product involving, i^2 or i^4. For example, i^3=i^2*i=(-1)*i=-i, Also, i^4=i^2*i^2=(-1)(-1)=1. Using i^4 and i^3 to rewrite i^15 gives
i^15=i^12*i^3=(i^4)^3*i^3=(1)^3(-i)=-i
(b) i^-3=i^-4*i=(i^4)^-1*1=(1)^-1*i=i
We can use the method of Example 8 to construct the following table of powers of i.
POWERS OF i
i^1=i i^5=i i^9=i
i^2=-1 i^6=-1 i^10=-1
i^3=-i i^7=-i i^11=-i
i^4=1 i^8=1 i^12=1 and so on.
Example 7(c) showed that (6 + 5i)(6 - 5i) = 61. The numbers 6 + 5i and 6 - 5i differ only in their middle signs; for this reason these numbers are called conjugates of each other. The product of a complex number and its conjugate is always a real number.
PROPERTY OF COMPLEX CONJUGATES
For real numbers a and b:
(a+bi)(a-bi)=a^2+b^2.
Example 9.
EXAMINING CONJUGATES AND THEIR PRODUCTS
The following list shows several pairs of conjugates, together with their products.
| Number | Conjugate | Product |
| 3-i | 3+i | (3-i)(3+i)=9+1=10 |
| 2+7i | 2-7i | (2+7i)(2-7i)=53 |
| -6i | 6i | (-6i)(6i)=36 |
The conjugate of the divisor is used to find the quotient of two complex numbers. The quotient is found by multiplying both the numerator and the denominator by the conjugate of the denominator. The result should be written in standard form.
Example 10.
DIVIDING COMPLEX NUMBERS
(a) Find (3+2i)/(5-i)
Multiply numerator and denominator by the conjugate of 5-i.
(3+2i)/(5-i)
=((3+2i)(5+i))/((5-i)(5+i))
=(15+3i+10i+2i^2)/(25-i^2) Multiply.
=(13+13i)/(26) i^2=-1
=13/26+(13i)/(26) (a+bi)/c=a/c+(bi)/c
=1/2+1/2i lowest terms
To check this answer, show that
(5-i)(1/2+1/2i)=3+2i
(b) 3/i
=(3(-i))/(i(-i)) -i is the conjugate of i.
=(-3i)/(-i^2)
=(-3i)/1 -i^2=-(-1)=1
=-3i or 0-3i Standard form