Exponents and Polynomials, Addition, Subtraction and Multiplication of Polynomials, Special Products of Binomials

4.1  Exponents and Polynomials

  In Section 1.2 we defined an exponent as a number that tells how many times a factor occurs in a product. In fact, this definition applies to natural-number exponents only. Negative-integer exponents are discussed in Appendix I and, along with fractional exponents, are a major topic in intermediate algebra. In this section we will discuss the meaning of a° and multiplication with algebraic terms that have whole-number exponents.

  Study the following examples carefully.

  6^2*6^3=(6*6)*(6*6*6)=6^5

  3^4*3^3=(3*3*3*3)*(3*3*3)=3^7

  x^2*x^4=(x*x)*(x*x*x*x)=x^6

  2y*3y^6=2*3*y(y*y*y*y*y*y)=6y^7

  (If a variable or constant has no exponent, it is understood to be 1; that is, y=y^1and 2=2^1.) 

  The preceding examples lead to the following property of exponents.

  Property 1 of Exponents
  If a is a nonzero integer and m and n are whole numbers, then

  a^m*a^n=a^(m+n)

  We may use whole~number exponents when Property 1 is used. Therefore, we need to know the meaning of 2^0, or 3^0, or a^0. Consider the following applications of Property 1 and the corresponding equations to the right.

  2^0*2^3=2^(0+3)=2^3  1*2^3=2^3 or 1*8=8

  3^0*3^4=3^(0+4)=3^4  1*3^4=3^4 or 1*81=81

  5^0*5^2=5^(0+2)=5^2  1*5^2=5^2 or 1*25=25

  7^0*7^2=7^(0+2)=7^2  1*7^2=7^2 or 1*49=49

  Does it seem reasonable to you that 2^0=1, 3^0=1, 5^0=1, and 7^0=1'? These must all be true if Property 1 is to be used with whole number exponents.

  Property 2 of Exponents

  If a is a nonzero integer, then

    a^0=1

  The expression 0^0 is undefined.

  A monomial is a single term with only whole-number exponents for its variables and no variable in a denominator. The general form of a monomial in x is

    kx^n where n is a whole number
n is called the degree of the monomial. A monomial may have more than one variable, but only monomials with one variable will be discussed in this section. In the case of a constant, such as 6, since 6=6*1=6x^0, we say that a constant is a monomial of 0 degree. As a special case, since 0=0x^0=0x^2=0x^7, we say that 0 is a monomial with no degree. Examples of monomials are

    13x^7,1/2x^2,2y^5 and 10

  Terms that are not monomials are
  2x^-1 negative exponent
  x^(1/2) fractional exponent
  3/x^2 variable in the denominator

  Any monomial or algebraic sum of monomials is a polynomial. For example, 3x,x+5, and a^2+5a-7 are all polynomials.
  

Classification of Polynomials

  monomial - polynomial with one term

  binomial - polynomial with two terms

  trinomial - polynomial with three terms

    Polynomials can be simplified by combining like terms.

Examples

  Simplify the following polynomials by combining like terms

  1. 5x^3+7x^3=(5+7)x^3=12x^3

  2. 2x^2-8x^2+3x+x=-6x^2+4x

  3. 1/2y+3y-2/3y^2-7=-2/3y^2+7/2y-7

  4. x^2+7x-x^2-7x=0

  The degree of a polynomial is the largest of the degrees of its terms. In the Practice Quiz, Problem 1 is a first-degree polynomial and Problems 2, 3, and 4 are all second-degree polynomials.

4.2  Adding and Subtracting Polynomials

  The sum of two or more polynomials is found by combining like terms. For example,

  (x^2-5x+3)+(2x^2-8x-4)+(3x^3+x^2-5)

  =3x^3+(x^2+2x^2+x^2)+(-5x-8x)+(3-4-5)

  =3x^3+4x^2-13x-6

  We can also write like terms one beneath the other and add the like terms in each column.

    

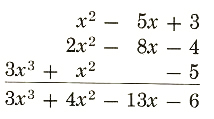
  If a negative sign is written in front of a polynomial in parentheses, the meaning is the opposite of the entire polynomial. The opposite can be found by changing the sign of every term in the polynomial.

  -(2x^2+3x-7)=-2x^2-3x+7

  We can also think of the opposite of a polynomial as -1 times the polynomial.

  -(2x^2+3x-7)=-1(2x^2+3x-7)

    =-1(2x^2)-1(3x)-1(-7)

    =-2x^2-3x+7

  The result is the same with either approach. So the difference between two polynomials can be found by changing the sign of each term of the second polynomial, then combining like terms.

  (5x^2-3x-7)-(2x^2+5x-8)

  =5x^2-3x-7-2x^2-5x+8

  =3x^2-8x+1

  If the polynomials are written one beneath the other, we change the signs of the terms of the polynomial being subtracted, then combine like terms. Subtract:

    

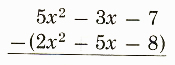
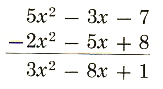
Examples

  1. Add.

  (5x^3+8x^2+12x+13)+(-2x^2-8)+(4x^3-5x+14)

  =9x^3-10x^2+7x+19

  2. Subtract.

  (9x^4-22x^3+3x^2+10)-(5x^4+2x^3+5x^2-x)

  =9x^4-22x^3+3x^2+10-5x^4-2x^3-5x^3+5x^2+x

  =4x^4-24x^3-2x^2+x+10

Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples. 

  

If an expression contains more than one pair of grouping (or inclusion) symbols such as parentheses ( ), brackets [ ], or braces { ), simplify by removing the innermost pair of symbols first. For example,

  5x-[2x+3(4-x)+1)]-9

  =5x-[2x+12-3x+1]-9  parentheses first

  =5x-[-x+13]-9

  =5x+x-13-9  brackets second

  =6x-22

4.3  Multiplying Polynomials

  We have multiplied terms such as 5x^2*3x^4=15x^6. Also, we have applied the distributive property to expressions such as 5(2x+3)=10x+15. Now we will use both of these procedures to multiply polynomials. First we will discuss the product of a monomial with a polynomial of two or more terms, then the product of two binomials, then the product of a binomial with a polynomial of more than two terms.

  Using the distributive property a(b+c)=ab+ac, we can find the product of a monomial with a polynomial of two or more terms as follows:

  5x(2x+3)=5x*2x+5x*3=10x^2+15x

  3x^2(4x-1)=3x^2*4x+3x^2(-1)=12x^3-3x^2

  -4a^5(a^2-8a+5)=-4a^5*a^2-4a^5(-8a)-4a^5(5)

  =4a^7+32a^6-20a^5

  Now suppose that we want to multiply two binomials, say (x + 3)(x + 7). We will apply the distributive law in a very subtle way.

  Compare  (x + 3)(x + 7)

  to  a(b+c)

  Think of (x + 3) as taking the place of a. Thus,

  takes the form 

     

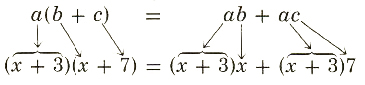
  Completing the products on the right, using the distributive property twice again, gives

  (x+3)(x+7)=(x+3)x+(x+3)7

    =x^2+3x+x*7+3*7

    =x^2+3x+7x+21

    =x^2+10x+21

  In the same manner,

  (x+2)(3x+4)=(x+2)3x+(x+2)4

    =x*3x+2*3x+x*4+2*4

    =3x^2+6x+4x+8

    =3x^2+10x+8

Let’s see how our polynomial solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  Similarly,

  (2x-1)(x^2+x-5)=(2x-1)x^2+(2x-1)x+(2x-1)(-5)

    =2x*x^2-1*x^2+2x*x-1*x+2x(-5)-1(-5)

    =2x^3-x^2+2x^2-x-10x+5

    =2x^3+x^2-11x+5

  One quick check to see if your products are correct is to substitute some convenient number for x into the original two factors and into the product. The results should be the same for all numbers. So choose any one you like. For example, let x=1.

  (x+2)(3x+4)=(1+2)(3*1+4)=(3)(7)=21

  3x^2+10x+8=3*1^2+10*1+8=3+10+8=21

  The product (x + 2)(3x + 4) = 3x^2 + 10x + 8 seems to be correct. We could double check by letting x = 5.

  (x+2)(3x+4)=(5+2)(3*5+4)=(7)(19)=133

  3x^2+10x+8=3*5^2+10*5+8=75+50+8=133

  Convinced? This is just a quick check, however, and is not foolproof unless you try more numbers than the degree of the product.

4.4  Special Products of Binomials

  Certain types of products of binomials occur so frequently in algebra that they deserve special mention. Their basic forms (or formulas) should be memorized. The forms are these:

  I.  (x+a)(x+b)=x^2+(a+b)x+ab

  II.  (x+a)(x-a)=x^2-a^2

  III  (x+a)^2=x^2+2ax+a^2

  IV  (x-a)^2=x^2-2ax+a^2

    I.  (x+a)(x+b)=x^2+(a+b)x+ab

  Consider the product

    (x+4)(x+6)=(x+4)x+(x+4)6

      =x^2+4x+6x+24

      =x^2+(4+6)x+24

      =x^2+10x+24

  In this example, a = 4 and b = 6. Note that a + b=10 and a*b=24. With practice, you should be able to go directly to the answer by working mentally.

  (x+7)(x+8)=x^2+(7+8)x+7*8  Here, a=7 and b=8.

    =x^2+15x+56

a and b can be negative as well as positive. The basic form still applies, (x-7)(x+8)=x^2+(-7+8)x+(-7)8

Here, a=-7 and b=8

    =x^2+x-56

     

  (x+7)(x-8)=x^2+(7-8)x+7(-8)  Here, a=7 and b=-8

    =x^2-x-56

    II.  (x+a)(x-a)=x^2-a^2

  The result, x^2-a^2, is the difference of two squares.

   Consider the product as a special case of (x+a)(x+b) where b=-a.

  (x+5)(x-5)=x^2+(5-5)x+5(-5)

    =x^2+0x-25

    =x^2-25

  (x+8)(x-8)=x^2-8^2=x^2-64

  (x-9)(x+9)=x^2-9^2=x^2-81

    III  (x+a)^2=x^2+2ax+a^2

  The result, x^2+2ax+a^2, is called a perfect square trinomial because it is the square of a binomial.
  Consider the product as a special case of (x + a)(x + b) where b=a.

  (x+5)(x+5)=x^2+(5+5)x+5*5

    =x^2+2*5*x+5^2

    =x^2+10x+25

  (x+7)(x+7)=x^2+14x+49

  (x+10)(x+10)=x^2+20x+100

  One interesting device that might help in remembering (x+a)^2=x^2+2ax+a^2 is the square shown in Figure 4.1. The area of

  

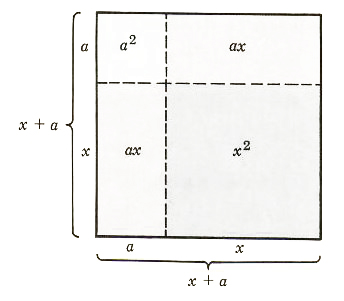
  Figure 4.1

  the square is (x + a)^2 because each side has length x + a. But the area is also equal to the sum of the areas of the smaller rectangles and squares inside the large square, namely.

  x^2+ax+ax+a^2, or (x+a)^2=x^2+2ax+a^2

  IV  (x-a)^2=x^2-2ax+a^2

  The result, x^2-2ax+a^2, is also called a perfect square trinomial.

  (x-5)(x-5)=x^2+(-5-5)x+(-5)(-5)

    =x^2-2(5)x+(-5)^2

    =x^2-10x+25

  (x-7)(x-7)=x^2-14x+49

  (x-10)(x-10)=x^2-20x+100

  In the special cases noted by formulas I, II, III, and IV, the coefficient of x in each binomial was 1. If either coefficient is not 1, the following technique for multiplying binomials is useful.

  (2x+3)(5x+2)=(2x+3)5x+(2x+3)^2

    =2x*5x+3*5x+2x*2+3*2

    

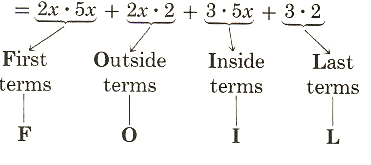
  This technique, illustrated by the following diagramed equations, is called the FOIL method of mentally multiplying two binomials.

  

  

  

  

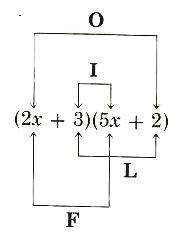
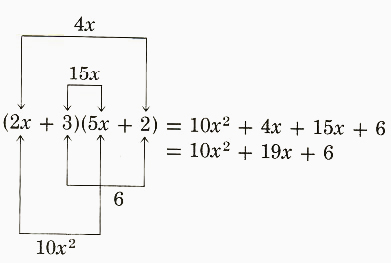
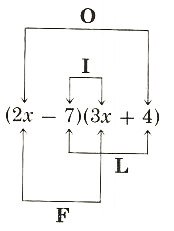
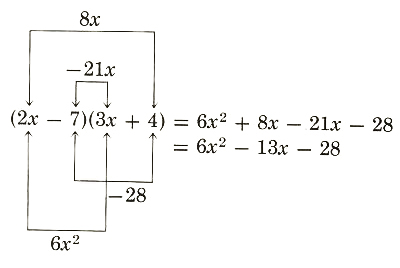
  In all the formulas, I, II, III, and IV, the student must understand that the letters are placeholders and x or a or b may be replaced by other terms. For example, formula II applies to the product

  (3y+5)(3y-5)=(3y)^2-5^2=9y^2-25

  Similarly, formula III applies to

  (3y+5)^2=(3y)^2+2*5*3y+5^2

    =9y^2+30y+25

and (y^3+1)^2=(Y^3)^2+2*1*y^3+1^2

    =y^6+2y^3+1

  Although all four formulas can be considered as special cases of the FOIL method, they still should be memorized.