Quadratic equations, it's applications and other type of equations

QUADRATIC EQUATIONS

  As mentioned earlier, an equation of the form ax + b = 0 is a linear equation. A quadratic equation is defined as follows.

QUADRATIC EQUATION IN ONE VARIABLE

  An equation that can be written in the form

  ax^2+bx+c=0,

  where a,b, and c are real numbers with a!=0, is a quadratic equation.

  (Why is the restriction a!=0 necessary?) A quadratic equation written in the form ax^2+bx+c=0 is in standard form.

  The simplest method of solving a quadratic equation, but one that is not always easily applied, is by factoring. This method depends on the following property.

ZERO FACTOR PROPERTY

  If a and b are complex numbers, with ab = 0, then a = 0 or b=0 or both

  The next example shows how the zero-factor property is used to solve a quadratic equation.

Example 1.

USING THE ZERO FACTOR PROPERTY

  Solve 6r^2+7r=3.

  First write the equation in standard form as

  6r^2+7r-3=0.

  Now factor 6r^2+7r-3 to get

  (3r-1)(2r+3)=0

  By the zero-factor property, the product (3r -1)(2r + 3) can equal 0 only if

  3r-1=0  or  2r+3=0

  Solve each of these linear equations separately to find that the solutions of the original equation are 1/3 and -3/2. Check these solutions by substituting in the original equation. The solution set is (1/3, -3/2). 

  A quadratic equation of the form x^2 = k can be solved by factoring with the following sequence of equivalent equations.

  x^2=k

  x^2-k=0

  (x-root(k))(x+root(k))=0

  x=root(k)=0  or  x+root(k)=0

  x=root(k)  or  x=-root(k)

  This proves the following statement. which we call the square root property.

SQUARE ROOT PROPERTY  The solution set of x^2=k is {root(k)-root(k)}.

  This solution set is often abbreviated as {+-root(k)}. Both solutions are real if k > 0 and imaginary if k < 0. (If k = 0, there is only one distinct solution, sometimes called a double solution.)

Example 2.

USING THE SQUARE ROOT PROPERTY

  Solve each quadratic equation.

  (a) z^2=17

  The solution set is {+-root(17)}.

  (b) m^2=-25

  Since root(-25)=5i, the solution set of m^2=-25 is {+-5i}.

  (c) (y-4)^2=12

  Use a generalization of the square root property, working as follows.

   (y-4)^2=12

  y-4=+-root(12)

  y=4+-root(12)

  y=4+-2root(3)

  The solution set is {4+-2root(3)}.

  COMPLETING THE SQUARE:  As suggested by Example 2(c), any quadratic equation can be solved using the square root property if it is first written in the form (x + n)^2 = k for suitable numbers n and k. The next example shows how to write a quadratic equation in this form.

Example 3.

USING THE METHOD OF COMPLETE THE SQUARE

  Solve x^2-4x=8

  To write x^2-4x=8 in the form (x + n)^2 = k, we must find a number that can be added to the left side of the equation to get a perfect square. The equation (x + n)^2 = k can be written as x^2 + 2xn + n^2 = k. Comparing this equation with x^2 - 4x = 8 shows that

  2xn=-4x

  n=-2

  If n = -2, then n^2 = 4. Adding 4 to both sides of x^2- 4x = 8 and factoring on the left gives

  x^2-4x+4=8+4

  (x-2)^2=12

  Now the square root property can be used as follows

  x-2=+-root(12)

  x=2+-2root(3)

  The solution set is {2+-2root(3)}.

  The steps used in solving a quadratic equation by completing the square follow.

SOLVING BY COMPLETING THE SQUARE

  To solve ax^2 + bx + c = 0, a!=0, by completing the square:

  1. If a!=1, multiply both sides of the equation by 1/a.

  2. Rewrite the equation so that the constant term is alone on one side of the
equals sign.

  3. Square half the coefficient of x, and add this square to both sides of the
equation.

  4. Factor the resulting trinomial as a perfect square and combine terms on the
other side.

  5. Use the square root property to complete the solution.

Example 4.

USING THE METHOD OF COMPLETING THE SQUARE

  Solve 9z^2-12z-1=0.

  The coefficient of z^2 must be 1. Multiply both sides by 1/9.

  z^2-4/3z-1/9=0

  Now add 1/9 to both sides of the equation.

  z^2-4/3z=1/9

  Half the coefficient of z is -2/3, and (-2/3)^2 = 4/9. Add 4/9 to both sides, getting

  z^2-4/3z+4/9=1/9+4/9.

  Factoring on the left and combining terms on the right gives

  (z-2/3)^2=5/9.

  Now use the square root property and the quotient property for radicals lo get

  z-2/3=+-root(5/9)

  z-2/3=+-root(5)/(3)

  z=2/3+-(root(5))/(3).

  These two solutions can be written as

  (2+-root(5))/(3)

  with the solution set abbreviated as {(2+-root(5))/(3)}.

This is how our quadratic equation step by step solver solves the problem above. You can see similar problems solved by clicking on 'Solve similar' button.

QUADRATIC FORMULA  The method of completing the square can be used to solve any quadratic equation. However, in the long run it is better to start with Lhe general quadratic equation,

  ax^2+bx+c=0  a!=0,

  and use the method of completing the square to solve this equation for x in terms of the constants a, b, and c. The result will be a general formula for solving any quadratic equation. For now, assume that a > 0 and multiply both sides by 1/a to get

  x^2+b/ax+c/a=0

  Add -c/a to both sides

  x^2+b/ax=-c/a

  Now take half of b/a, and square the result:

  1/2*b/a=b/(2a)  and  (b/(2a))^2=(b^2)/(4a^2).

  Add the square to both sides, producing

  x^2+b/ax+(b^2)/(4a^2)=(b^2)/(4a^2)-c/a.

  The expression on the left side of the equals sign can be written as the square of a binomial, while the expression on the right can be simplified.

  (x+b/(2a))^2=(b^2-4ac)/(4a^2)

  By the square root property, this last statement leads to

  x+b/(2a)=root((b^2-4ac)/(4a^2))  or  x+b/(2a)=-root((b^2-4ac)/(4a^2))

  Since 4a^2=(2a)^2, or 4a^2=(-2a)^2,

  x+b/(2a)=(root(b^2-4ac))/(2a) or x+b/(2a)=(-root(b^2-4ac))/(2a)

  Adding -b/((2a)) to both sides of each result gives

  x=(-b+root(b^2-4ac))/(2a) or x=(-b-root(b^2-4ac))/(2a)

  It can be shown that these two results are also valid if a < 0. A compact form of these two equations. called the quadratic formula, fellows.

QUADRATIC FORMULA  The solutions of the quadratic equation ax^2+bx+c=0, where a!=0, are

  (-b+-root(b^2-4ac))/(2a)

CAUTION  Notice that the fraction bar in the quadratic formula extends under the -b term in the numerator.

Example 5.

USING QUADRATIC FORMULA (REAL SOLUTIONS)

  Solve x^2-4x+2=0

  Here a = 1 ,b = -4. and c = 2. Substitute these values into the quadratic formula to get

  x=(-b+-root(b^2-4ac))/(2a)

  =(-(-4)+-root((-4)^2-4(1)2))/(2(1))  a=1,b=-4,c=2

  =(4+-root(16-8))/(2)

  =(4+-2root(2))/(2)  root(16-8)=root(8)=2root(2)

  =(2(2+-root(2)))/(2)  Factor out a 2 in the numerator.

  =2+-root(2)  Lowest terms

  The solution set is {2+root(2),2-root(2)}, abbreviated as {2+-root(2)}.

Example 6.

USING THE QUADRATIC FORMULA (COMPLEX SOLUTIONS)

  Solve 2y^2=y-4

  To find the values of a, b, and c, first rewrite the equation in standard form as 2y^2 - y + 4 = 0. Then a = 2, b = -1, and c = 4. By the quadratic formula,

  y=(-(1)+-root((-1)^2-4(2)(4)))/(2(2))

  =(1+-root(1-32))/(4)

  =(1+-root(-31))/(4)

  =(1+-(i)root(31))/(4)

  The solution set is {1/4+-((i)root(31))/(4)}.

  The equation in Example 7 is called a cubic equation, because of the term of degree 3. In Chapter 6 we will discuss such higher degree equations in more detail. However, the equation x^3 + 8 = 0, for example, can be solved using factoring and the quadratic formula.

Example 7.

USING THE QUADRATIC FORMULA IN SOLVING A PARTICULAR CUBIC EQUATION

  Solve x^3+8=0.

  Factor on the left side, and then set each factor equal to zero.

  x^3+8=0

  (x+2)(x^2-2x+4)=0

  (x+2)=0  or  x^2-2x+4=0

  The solution of x + 2 = 0 is x = -2. Now use the quadratic formula to solve x^2-2x+4=0.

  x^2-2x+4=0

  x=(2+-root(4-16))/2)  a=1,b=-2,c=4

  x=(2+-root(-12))/(2)

  x=(2+-2i(root(3)))/(2)

  x=1+-(i)root(3)  Factor out a 2 in the numerator and reduce to lowest terms.

  The solution set is {-2,1+-(i)root(3)}.

Let’s see how our cubic equation solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  Sometimes it is necessary to solve a literal equation for a variable that is squared. In such cases, we usually apply the square root property of equations or the quadratic formula.

Example 8.

SOLVING FOR A VARIABLE IS SQUARED

  (a) Solve for d: A=(PId^2)/(4).

  Start by multiplying bath sides by 4 to get

  4A=PId^2

  Now divide by PI.

  d^2=(4A)/(PI)

  Use the square root properly and rationalize the denominator on the right.

  d=+-root((4A)/(PI))

  d=(+-2root(A))/(root(PI))

  d=(+-2root((A)PI))/(PI)

  (b) Solve for t: rt^2-st=k(r!=0).

  Because this equation has a term with t as Well as t^2, we use the quadratic formula. Subtract k from both sides to get

  rt^2-st-k=0.

  Now use the quadratic formula to find t, with a=r,b=-s, and c=-k.

  t=(-b+-root(b^2-4ac))/(2a)

  t=(-(-s)+-root((-s)^2-4(r)(-k)))/(2(r))

  t=(s+-root(s^2+4rk))/(2r)

NOTE  In practical applications of formulas solved for a squared variable, it is often necessary to reject one of the solutions because it does not satisfy the physical conditions of the problem.

  THE DISCRIMINANT The quantity under the radical in the quadratic formula, b^2 - 4ac, is called the discriminant. When the numbers a,b, and c are integers (but not necessarily otherwise), the value of the discriminant can be used to determine whether the solutions will be rational, irrational, or imaginary numbers. If the discriminant is 0, there will be only one distinct solution. (Why?)

  The discriminant of a quadratic equation gives the following information about the solutions of the equation.

DISCRIMINANT

Discriminant	Number of Solutions	Kind of Solutions
Positive. perfect square	Two	Rational
Positive, but not a perfect square	Two	Irrational
Zero	One (a double solution)	Rational
Negative	Two	Imaginary

Example 9

USING THE DISCRIMINANT

  Use the discriminant to determine whether the solutions of 5x^2+2x-4=0 are rational. irrational, or imaginary.

  The discriminant is

  b^2-4ac=(2)^2-(4)(5)(-4)=84

  Because the discriminant is positive and a,b, and c are integers, there are two real-number solutions. Since 84 is not a perfect square, the solutions will be irrational numbers. 

Example 10.

USING THE DISCRIMINANT

  Find all values of k so that the equation

  16p^2+kp+25=0

  has exactly one solution.

  A quadratic equation with real coefficients will have exactly one solution if the discriminant is zero. Here, a=16, b = k, and c = 25, giving the discriminant

  b^2-4ac=k^2-4(16)(25)=k^2-1600

  The discriminant is 0 if

  k^2-1600=0

  k^2=1600

  from which k = +-40.

  Recall from Section 1.6 that a rational expression is not defined when its denominator is 0. Restrictions on the variable are found by determining the value or values that cause the expression in the denominator to equal 0.

Example 11.

DETERMINING RESTRICTIONS ON THE VARIABLE

  For each of the following, give the real number restrictions on the variable.

  (a) (2x-5)/(2x^2-9x-5)

  Set the denominator equal to 0 and solve.

  2x^2-9x-5=0

  (2x+1)(x-5)=0

  2x+1=0  or  x-5=0

  x=-1/2  or  x=5

  The restrictions on the variable are x!=-1/2 and x!=5.

  (b) 1/(3x^2-x+4)

  Solve 3x^2-x+4=0. Since the polynomial does not factor, use the quadratic formula.

  x=(-(-1)+-root((-1)^2-4(3)(4)))/(2(3))=(1+-root(-47))/(6)

  Both solutions are imaginary numbers, so there are no real numbers that make the denominator equal to zero. Thus there are no real number restrictions on x.

2.5  APPLICATIONS OF QUADRATIC EQUATIONS

  Many applied problems lead to quadratic equations. In this section we give examples of several kinds of such problems.

CAUTION  When solving problems that lead to quadratic equations, we may get a solution that does not satisfy the physical constraints of the problem. For example, if x represents a width and the two solutions of the quadratic equation are -9 and 1. the value -9 must be rejected, since a width must be a positive number.

Example 1

SOLVING A GEOMETRY PROBLEM

  A landscape contractor wants to make an exposed gravel border of unifonn width around a rectangular pool in a garden. The pool is 10 feet long and 6 feet wide. There is enough material to cover 36 square feet. How wide should the border be?

  A diagram of the pool with the border is shown in Figure 2.4. Since we are asked to find the width of the border, let

  x= the width of the border in feet.

  Then  6+2x= the width of the larger rectangle in feet,

  and  10+2x= the length of the larger rectangle in feet.

  

  

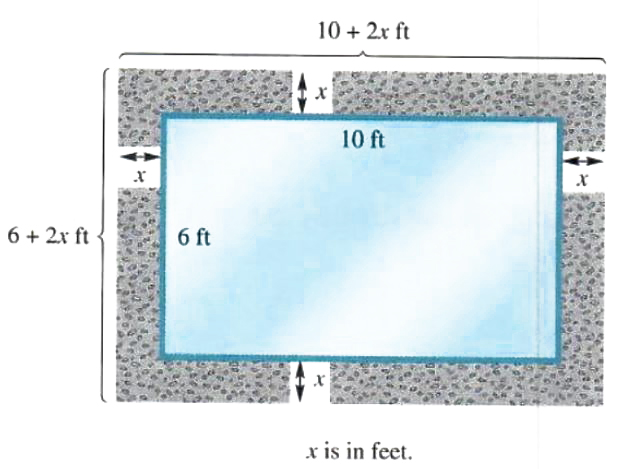
  The area of the larger rectangle is (6+2x)(10+2x) square feet, and the area of the pool is 6 *10 = 60 square feet The area of the border is found by subtracting the area of the pool from the area of the larger rectangle. This difference should be 36 square feet.

  

Area of the larger rectangle	minus	area of the pool	is	36 square feet.
(6+2x)(10+2x)	-	60	=	36

  Now solve this equation.

  60+32x+4x^2-60=36

  4x^2+32x-36=0

  x^2+8x-9=0

  (x+9)(x-1)=0

  The solutions are -9 and 1. The width of the border cannot be negative. so the border should be 1 foot wide. 

  Problems involving rate of work were first introduced in Section 2.2. Recall that if a job can be done in x units of lime, the rate of work is 1/x job per unit of time.

Example 2

SOLVING A WORK PROBLEM

  Pat and Mike clean the offices in a downtown office building each night. Working alone. Pat takes 1 hour less time than Mike to complete the job. Working together, they can finish the job in 6 hours. One night Pa! calls in sick. How long should it take Mike to do the job alone?

  Let

  x= the time for Mike to do the job alone

  and

  x-1= the time for Pat to do the job alone.

  The rates for Mike and Pat are. respectively. 1/x and 1/(x - 1) job per hour. If we multiply the time worked together, 6 hours, by each rate, we gel the fractional pan of the job done by each person. This is summarized in the following chart.

  

	Rate	Time	Part of the
Mike	1/x	6	6(1/x)=6/x
Pat	1/(x - 1)	6	6(1/(x-1))=6/(x-1)

  Since one whole job can be done by the two people, the sum of the pans must equal 1, as indicated by the equation

  6/x+6/(x-1)=1

  To clear fractions, multiply both sides of the equation by the least common denominator, x(x - 1).

  x(x-1)6/x+x(x-1)6/(x-1)=1x(x-1)

  6*(x-1)+6x=x(x-1)

  6x-6+6x=x^2-x

  0=x^2-13x+6

  x=(13+-root((-13)^2-4(1)(6)))/(2(1))  a=1,b=-13,c=6

  x=(13+-root(169-24))/(2)

  x=(13+-root(145))/(2)

  x≈(13+-12.04)/(2)

  Use a calculator to find that to the nearest tenth, x = 12.5 or x = 0.5. The solution x = 0.5 does not satisfy the conditions of the problem, since then Pat takes x - 1 = -0.5 hour to complete the work. It will take Mike 12.5 hours to do the job alone. 

Example 3

SOLVING A MOTION PROBLEM

  A river excursion boat traveled upstream from Galt to Isleton. a distance of 12 miles. On the return trip downstream, the boat traveled 3 miles per hour faster. If the return trip took 8 minutes less time, how fast did the boat travel upstream?

  The chart below summarizes the information in the problem, where x represents the rate upstream.

   

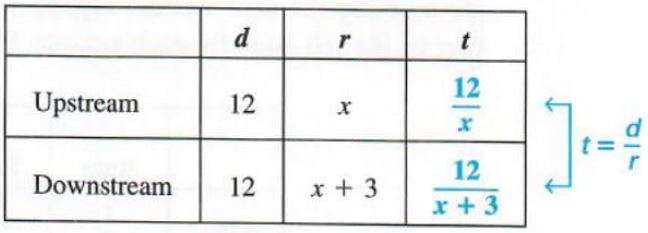
  The entries in the column for time are found from solving the distance formula. d = rt, for t in each case. Since rates are given in miles per hour, convert 8 minutes to hours as follows, letting H represent the equivalent number of hours.

  (Hhr)/(1hr)=(8 min)/(60min)

  H=8/60=2/15

  Now write an equation using the fact that the time for the return trip (downstream) was 8 minutes or 2/15 hour less than the time upstream.

Time downstream	is	time upstream	less	2/15 hour
12/(x+3)	=	12/x	-	2/15

  Solve the equation, first multiplying on both sides by the common denominator. 15x(x + 3), to get

  12(15)x=12(15)(x+3)-2x(x+3)

  180x=180x+540-2x^2-6x

  2x^2+6x-540=0  Standard form

  x^2+3x-270=0  Divide by 2.

  (x+18)(x-15)=0  

  x=-18  or  x=15

  Reject the negative solution. The boat traveled 15 miles per hour upstream.

CAUTION

  When problems involve different units of time (as in Example 3, where rate was given in miles per hour and time was given in minutes). it is necessary to convert to the same unit before setting up the equation.

PYTHAGOREAN THEOREM

  In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.

  a^2+b^2=c^2

   

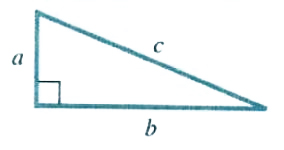
Example 4.

SOLVING A PROBLEM INVOLVING THE PYTHAGOREAN THEOREM

  A lo! is in the shape of a right triangle. The longer leg of the triangle is 20 meters longer than twice the length of the shorter leg. The hypotenuse is 10 meters longer than the longer leg. Find the lengths of the three sides of the lot.

  Let s = length of the shorter leg in meters. Then 2x + 20 meters represents the length of the longer leg, and (2s+20)+10=2s+30meters represents the length of the hypotenuse. See Figure 2.5

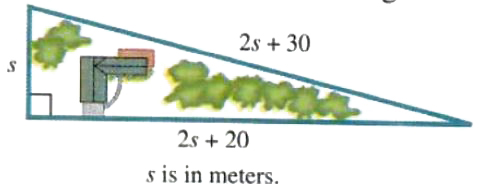
  FIGURE 2.5

  Application of the Pythagorean theorem gives the equation

  s^2+(2s+20)^2=(2s+30)^2

  s^2+4s^2+80s+400=4s^2+120s+900

  s^2-40s-500=0

  (s-50)(s+10)=0

  s=50  or  s=-10

  Since s represents a length, the value -10 is not reasonable. The shorter leg is 50 meters long, the longer leg 120 meters long, and the hypotenuse 130 meters long. 

IN SIMPLEST TERMS

  To determine the appropriate landing speed of an airplane, the formula 0.1s^2-3s+22=D is used, where s is the initial landing speed in feet per second and D is the distance needed in feet. If the landing speed is too fast, the pilot may run out of runway; if the speed is too slow, the plane may stall. Suppose the runway is 800 feet long. The appropriate landing speed may be calculated by completing the square. In the first step, multiply the equation by 10 to eliminate the decimal.

  0.1s^2-3s+22=800

  s^2-30s+220=8000

  s^2-30s=7780

  s^2-30s+225=8005

  (s-15)^2=8005

  s-15=+-root(8005)

  s=15+-root(8005)

  s≈15+-89.5

  The only realistic solution for the landing speed is approximately 104.5 feet per second.

Example 5

SOLVING A PROBLEM INVOLVING MOTION OF A PROJECTILE

  If a projectile is shot vertically upward with an initial velocity of 100 feet per second, neglecting air resistance, its height s (in feet) above the ground t seconds after projection is given by

  s=-16t^2+100t

  (a) After how many seconds will it be 50 feet above the ground?

  We must find the value of t so that s=50. Let s=50 in the equation, and use the quadratic formula.

  50=-16t^2+100t

  16t^2-100t+50=0  Standard form

  8t^2-50t+25=0  Divide by 2

  t=(-(-50)+-root((-50)^2-4(8)(25)))/(2(8))

  t=(50+-root(1700))/(16)

  t≈0.55  or  t≈5.70  use a calculator.

  Here, both solutions are acceptable. since the projectile reaches 50feat twice: once on its way up (after 0.55 second) and once on its way down (after 5.70 seconds).

  (b) How long will it take for the projectile to return to the ground?

  When it returns to the ground, its height s will be 0 feet, so let s = 0 in the equation.

  0=-16t^2+100t

  This can be solved by factoring.

  0=-4t(4t-25)

  -4t=0  or  4t-25=0

  t=0       4t=25

            t=6.25

  The first solution, 0, represents the time at which the projectile was on the ground prior to being launched, so it does not answer the question. The projectile will return to the ground 6.25 seconds after it is launched. 

OTHER TYPES OF EQUATIONS

  Many equations that are not actually quadratic equations can be solved by the methods discussed earlier in this chapter.

  EQUATIONS QUADRATIC IN FORM The equation 12m^4-11m^2+2=0 is not a quadratic equation because of the m^4 term. However, with the substitutions

  x=m^2  and  x^2=m^4

  the given equation becomes

  12x^2-11x+2=0

  which is a quadratic equation. This quadratic equation can be solved to find x, and then x = m^2 can be used to find the values of m, the solutions to the original equation.

QUADRATIC FORM

  An equation is said to be quadratic in form if it can be written as

  au^2+bu+c=0

  Where a!=0 and uis some algebraic expression.

Example 1

SOLVING AN EQUATION QUADRATIC IN FORM  

  Solve 12m^4-11m^2+2=0.

  As mentioned above, this equation is quadratic in form. By making the substitution x=m^2, the equation becomes

  12x^2-11x+2=0,

  which can be solved by factoring in the following way.

  12x^2-11x+2=0

  (3x-2)(4x-1)=0

  x=2/3  or  x=1/4

  The original equation contains the variable m. To find m, use the fact that x=m^2  and replace x with m^2, gelling

  m^2=2/3      or    m^2=1/4

  m=+-root(2/3)        m=+-root(1/4)

  m=+-root(2)/(root(3))*(root(3))/(root(3))

  m=+-(root(6))/(3)    or    m=+-1/2

  These four solutions of the given equation 12m^4-11m^2+2=0 make up the solution set {root(6)/3,-(root(6))/(3),1/2,-1/2}, abbreviated as {+-(root(6))/(3),+-1/2}.

NOTE

  Some equations that are quadratic in form, such as  the one in Example 1, can be solved quite easily by direct factorization. The polynomial there can be factored as (3m^2-2)(4m^2-1), and by setting each actor equal to zero the same solution set is obtained.  

Example 2.

SOLVING AN EQUATION QUADRATIC IN FORM

  Solve 6p^(-2)+p^(-1)=2.

  Let u=p^(-1) so that u^2=p^(-2). Then substitute and rearrange terms to get

  6u^2+u-2=0.

  Factor on the left, and then place each factor equal to 0, giving

  (3u+2)(2u-1)=0

  3u+2=0  or  2u-1=0

  u=-2/3  or  u=1/2

  Since u=p^(-1),  p^(-1)=-2/3  or  p^(-1)=1/2,

  from which  p=-3/2  or  p=2.

  The solution set of 6p^(-2)+p^(-1)=2 is {-3/2,2}.

CAUTION  When solving an equation that is quadratic in form, if a substitution variable is used, do not forget the step that gives the solution in terms of the original variable that appears in the equation.

  EQUATIONS WITH RADICALS OR RATIONAL EXPONENTS To solve equations containing radicals or rational exponents, such as x=root(15-2x), or (x+1)^(1/2)=x, use the following property.

  If P and Q are algebraic expressions, then every solution of the equation P = Q is also a solution of the equation (P)^n = (Q)^n, for any positive integer n.

CAUTION  Be very careful when using this result. It does not say that the equations P=Q and (P)^n = (Q)^n are equivalent: it says only that each solution of flue original equation P=Q is also a solution of the new equation (P)^n = (Q)^n.

  When using this property to solve equations, we must be aware that the new equation may have more solutions than the original equation. For example, the solution set of the equation x = -2 is {-2}. If we square both sides of the equation x = -2, we get the new equation x^2=4, which has solution set {-2,2}. Since the solution sets are not equal, the equations are not equivalent. Because of this, when an equation contains radicals or rational exponents, it is essential to check all proposed solutions in the original equation.

Example 3.

SOLVING AN EQUATION CONTAINING A RADICAL

  Solve x=root(15-2x).

  The equation x=root(15-2x)can be solved by squaring both sides as follows.

  x^2=(root(15-2x))^2

  x^2=15-2x

  x^2+2x-15=0

  (x+5)(x-3)=0

  x=-5  or  xx=3

  Now the proposed solutions must be checked in the original equation, x=root(15-2x).

  If

  x=-5

  x=root(15-2x)

  -5=root(15-2(-5))  ?

  -5=root(15+10)  ?

  -5=root(25)  ?

  -5=5  False

  If

  x=3

  x=root(15-2x)

  3=root(15-2(3))  ?

  3=root(15-6)  ?

  3=root(9)  ?

  3=3  True

  As this check shows, only 3 is a solution, giving the solution set {3}.

  To solve an equation containing radicals, follow these steps.

SOLVING AN EQUATION INVOLVING RADICALS

  1. Isolate the radical on one side of the equation.

  2. Raise each side of the equation to a power that is the same as the index of the radical so that the radical is eliminated.

  3. Solve the resulting equation. If it still contains a radical, repeat Steps 1 and 2.

  4. Check each proposed solution in the original equation.

Example 4.

SOLVING AN EQUATION CONTAINING TWO RADICALS

  Solve root(2x+3)-root(x+1)=1.

  When an equation Contains two radicals, begin by isolating one of the radicals on one side of the equation. For this one, let us isolate root(2x+3) (Step 1).

  root(2x+3)=1+root(x+1)

  Now square both sides (Step 2). Be very careful when squaring on the right side of this equation. Recall that (a+b)^2=a^2+2ab+b^2: replace a with 1 and b with root(x+1) to get the next equation, the result of squaring both sides of root(2x+3)=1+root(x+1).

  2x+3=1+2root(x+1)+x+1

  x+1=2root(x+1)

  One side of the equation still contains a radical; to eliminate it. square both sides again (Step 3).

  x^2+2x+1=4(x+1)

  x^2-2x-3=0

  (x-3)(x+1)=0

  x=3  or  x=-1

  Check these proposed solutions in the original equation (Step 4)

  Let x=3.

  root(2x+3)-root(x+1)=1

  root(2(3)+3)-root(3+1)=1  ?

  root(9)-root(4)=1  ?

  3-2=1  ?

  1=1  True

  Let x=-1

  root(2x+3)-root(x+1)=1

  root(2(-1)+3)-root(-1+1)=1  ?

  root(1)-root(0)=1  ?

  1-0=1  ?

  1=1  True

  Both proposed solutions 3 and -1 are solutions of the original equation, giving {3, -1} as the solution set. 

Example 5.

SOLVING AN EQUATION CONTAINING A RATIONAL EXPONENT

  Solve (5x^2-6)^(1/4)=x.

  Since the equation involves a fourth root, begin by raising both sides to the fourth power.

  [(5x^2-6)^(1/4)]^4=x^4

  5x^2-6=x^4

  x^4-5x^2+6=0

  Now substitute y for x^2.

  y^2-5y+6=0

  (y-3)(y-2)=0

  y=3  or  y=2

  Since y=x^2,

  x^2=3  or  x^2=2

  x=+-root(3)  or  x=+-root(2).

  Checking the four proposed solutions, root(3),-root(3),root(2) and -root(2) in the original equation shows that only root(3) and root(2) are solutions, so the solution set is {root(3),root(2)}. 

NOTE  In the equation of Example 5, we can use the fact that b^(1/4)=root(4,b) is a principal fourth root, and thus the right side, x, cannot be negative. Therefore. the two negative proposed solutions must be rejected.