Solving Quadratic Equations by factoring, applications and word problems

5.4  Solving Quadratic Equations by Factoring

  How would you solve the equation 5(x-2)=0? Would you proceed in either of the following ways?

  5(x-2)=0  

    (5(x-2))/5=0/5  

    x-2=0  

    x=2  

  5(x-2)=0

    5x-10=0

    5x=10

    (5x)/5=10/5

    x=2

  Both ways are correct and yield the solution x = 2. But did you think that x - 2 had to be 0? This is true because 5 * 0 = 0, and 0 is the only number multiplied by 5 that will give a product of 0. You could have written

  5(x-2)=0

    x-2=0

    x=2

  Now consider an equation involving a product of two polynomials such as

  (x-3)(x-2)=0

  If you multiply (x-3)(x-2), you get

  (x-3)(x-2)=0

  x^2-5x+6=0

  This procedure does not help because x^2-5x+6=0 is not any easier to solve than the original equation.

  Since we have a product that equals 0, we allow one of the factors to be 0. Which one? Choose x - 2.

  (x-3)(x-2)=0

    x-2=0

    x=2

Checking,

  (2-3)(2-2)=0

    (-1)(0)=0

  So, 2 is one solution.

  Suppose we choose to let x-3=0.

  (x-3)(x-2)=0

    x-3=0

    x=3

Checking,

  (3-3)(3-2)=0

    0(1)=0

  So, 3 is also a solution.
Thus, to solve an equation involving a product of polynomials equal to 0, we can let each factor in turn equal 0 to find all possible solutions. The reason is that a product is 0 only if at least one of the factors is 0.

  If a*b=0, then a=0 or b=0

Example

  Solve the following equations.

  1. (x-5)(x+4)=0

    (x-5)=0  or  x+4=0

    x=5        x=-4

  2. x(x-3)=0

    x=0  or  x-3=0

             x=3

  Polynomials of second degree are called quadratics. Equations of the form

  ax^2+bx+c=0  (a!=0)

  are called quadratic equations.

  Factoring the quadratic expression, when possible, gives two factors of first degree. Putting each factor equal to 0 gives two first-degree equations that can easily be solved. Each of these solutions is a solution of the quadratic equation.

  Not all quadratics can be factored using integer coefficients. Using techniques other than factoring to solve quadratic equations is discussed in Chapter 10.

Examples

  Solve the following quadratic equations by factoring.

  1. x^2-7x+12=0

    (x-4)(x-3)=0

    x-4=0  or  x-2=0

    x=4       x=3

  2. x^2+9x=22

    x^2+9x-22=0  One side of the equation must be 0.

    (x+11)(x-2)=0

    x+11=0  or  x-2=0

    x=-11      x=2

  3. x^2-16x+64=0

    (x-8)^2=0

    x-8=0

    x=8

  Since both factors are the same, there is only one solution.

  4. x^2=11x-28

    x^2-11x+28=0

    (x-4)(x-7)=0

    x-4=0  or  x-7=0

    x=4      x=7

  5. 4x^2-4x-24=0

    4(x^2-x-6)=0

    4(x-3)(x+2)=0  The constant factor 4 can never be 0 and does not affect the solution.

    x-3=0  or  x+2=0

    x=3       x=-2

Let’s see how our equation solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  6. x^2/3+5x-18=0

    3*x^2/3+3*5x-3*18=3*0  Multiply each term on both sides of the equation by 3. If there is more than one denominator, multiply by the LCM of the denominators.

    x^2+15x-54=0

    (x+18)(x-3)=0

    x+18=0  or  x-3=0

    x=-18       x=3

5.5  Applications

  Whether or not word problems cause you difficulty depends a great deal on your personal experiences and general reasoning abilities. These abilities are developed over a long period of time. A problem that is easy for you, possibly because you have had experience in a particular situation, might be quite difficult for a friend, and vice versa.

  Most problems do not say specifically to add, subtract, multiply, or divide. You are to know from the nature of the problem what to do. You are to ask yourself. “What information is given?;” “What am I trying to find?;” and “What tools, skills, and abilities do I need to use?.”

  Word problems should be approached in an orderly manner. Have an “attack plan.”

  Attack Plan for Word Problems

  1. Read the problem carefully at least twice.

  2. Decide what is asked for and assign a variable to the unknown quantity.

  3. Organize a chart, or a table, or a diagram relating all the information provided.

  4. Form an equation. (Possibly a formula of some type is necessary.)

  5. Solve the equation.

  6. Check your solution with the wording of the problem to be sure it makes sense.

  Several types of problems lead to quadratic equations. The problems in this section are set up so the equations can be solved by factoring. More general problems and approaches to solving quadratic equations are discussed in Chapter 10.

Examples

  1. One number is four more than another, and the sum of their squares is 296. What are the numbers?

Solution:

  Let x= smaller number

  x+4= large number

  x^2+(x+4)^2=296  Add the squares.

  x^2+x^2+8x+16=296

  2x^2+8x-280=0

  x^2+4x-140=0  The constant factor 2 dues not

  (x+14)(x-10)=0  affect the solution.

  x+14=0  or x-10=0

  x=-14    x=10

  x+4=-10   x+4=14

  There are two sets of answers to the problem, 10 and 14 or -14 and -10. (10^2 +14^2 = 100 + 196 = 296 and (-14)^2 + (-10)^2 = 196 + 100 = 296.)

  2. In an orange grove, there are 15 more trees in each row than there are rows. How many rows are there if there are 406 trees in the grove?

Solution:

  Let x= number of rows

  x+15= number of trees per row

  x(x+15)=406

  x^2+15x=406

  x^2+15x-406=0

  (x-14)(x+29)=0

  x-14=0  or  x+29=0

  x=14         Extraneous solution because -29 does not fit the conditions of the problem even though -29 is a solution to the equation.

  There are 14 rows in the grove.

  ((14*29=406))

  3. A rectangle has an area of 135 square meters and a perimeter of 48 meters. What are the dimensions of the rectangle?

Solution:

  The area of a rectangle is the product of its length and width

  (A = lw)

  The perimeter of a rectangle is given by P = 2l + 2w.

  Since the perimeter is 48 meters, then the length plus the Width must
be 24 meters.

  Let w= width

  24-w= length

  w(24-w)=135  Area = width times length

  24w-w^2=135

  0=w^2-24w+135

  0=(w-9)(w-15)

  w-9=0  or  w-15=0

  w=9        w=15

  24-w=15     24-w=9

  

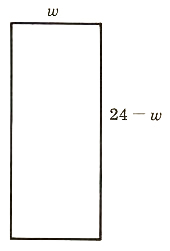
  The width is 99 meters and the length is 15 meters. ((9*15=135))

  4. A man wants to build a block wall along three sides of his property. If 252 feet of fencing are needed and the area of the lot is 6480 square feet, what are the dimensions of the lot?

Solution :

  Since only three sides of the lot are involved, if one of the two equal sides is x, then 252-2x will be the third side.

  Let x= one of two equal sides

  252-2x= third side

  

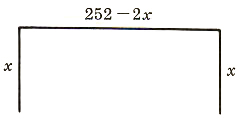
  x(252-2x)=6480

  252x-2x^2=6480

  0=2x^2-252x+6480

  0=x^2-126x+3240

  0=(x-90)(x-36)

  x-90=0  or  x-36=0

  x=90        x=36

  252-2x=72    252-2x=180

  The length is 90 feet and the width is 72 feet, or the length is 180 feet and the Width is 36 feet. (90 + 90 + 72 = 252,180 + 36 + 36 = 252.

  5. The sum of the squares of two positive consecutive even integers is 340. Find the integers.

Solution :

  Let n= first integer

  n+2= next consecutive even integer

  n^2+(n+2)^2=340

  n^2+n^2+4n+4=340

  2n^2+4n-336=0

  2(n^2+2n-168)=0

  2(n-12)(n+14)=0

  n-12=0  or  n+14=0

  n=12           The problem asked for positive integers.

  The first integer is 12 and the next consecutive even integer is 14. (12^22 + 14^2 = 144 + 196 = 340.)

5.6  Additional Applications (Optional)

The volume of a cylinder is given by the formula: V=PIr^2h
  V is the volume
  PI = 3.14 (3.14 is an approximation for PI)
  r is the radius
  h is the height
  1. Find the volume of a cylinder with a radius of 6 in. and a height of 20 in.
  2. Find the -height of a cylinder if the volume is 282.6 in. and the radius is 3 in.

  3. A cylinder has a height of 14 in. and a volume of 1099 cu in. Find the radius.
  4. Find the radius of a cylinder whose volume is 2512 cubic centimeters and whose height is 8 centimeters.
The safe load of a horizontal wooden beam supported at both ends is expressed by the formula L = kbd^2/l.
  L is expressed in pounds,
  b is the breadth or width in inches,
  d is the depth in inches,
  l is the length in inches, and
  k, a constant, depends on the grade of the beam and is expressed in pounds per square inch.

  5. What is the safe maximum load of a white pine beam 180 in. long, 3 in. wide, and 4 in. deep if k = 3000 lb per sq in.?
  6. Find the constant k if a beam 144 in. long, 2 in. wide, and Gin. deep supports a maximum load of 1100 lb.
  7. A solid oak beam is required to support a load of 12000 lb. It can be no more than 8 in. deep and is 192 in. long. For this grade of oak, k = 6000 lb per sq in. How wide should the beam be?

  8. The safe maximum of a white pine beam 4 in. wide and 150 in. long is 2880 lbs. For white pine, k = 3000 lb per sq in. Find the depth of the beam.

  9. A Douglas fir beam is required to support a load of 20000 lbs. For Douglas fir, k = 4800 lb per sq in. If the beam is Gin. wide and 144 in. long, what is the minimum depth for the beam to support the required load?

  The equation h=-16t^2+v_0t gives the height h, in feet, that a body will be above the earth at time t, in seconds, if it is projected upward with an initial velocity v_0 feet per second.

  10. Find the height of an object 3 seconds after it has been projected upward at a rate of 56 feet per second.

  11. Find the height of an object 5 seconds after it has been projected upward at a rate of 120 feet per second.

  12. A ball is thrown upward with a velocity of 144 feet per second. When will it strike the ground?

  13. An object is projected upward at a rate of 160 feet per second. Find the time when it is 384 feet above the ground.

  14. An object is projected upward at a rate of 96 feet per second. Find the time when it is 144 feet above the ground.

  The power output of a generator armature is given by the equation

  P_0=E_gI-r_gI^2

  where p_0, is measured in kilowatts, {Epsilon}_g is measured in volts, r_g is measured in ohms, and {Iota} is measured in amperes.

  15. Find {Iota} if P_0=120 kilowatts, {Epsilon}_g = 16 volts, and r_g=1/2 ohms.

  16. Find {Iota} if P_0=180 kilowatts, {Epsilon}_g=22 volts, and r_g=2/3 ohms.

  The demand for a product is the number of units of the product that consumers
are willing to buy when the market price is p dollars The consumers’ total expenditure for the product is found by multiplying the price times the demand.

  17. When fishing reels are priced at p dollars, local consumers will buy 36 - p fishing reels. What is the price if total sales were $320?

  18. A manufacturer can sell 100 - 2p lamps at p dollars each. If the total receipts from the lamps is $1200, what is the price of the lamps?

  The demand for a certain commodity is given by D = -20p^2+ap+1200 units per month, where p is the selling price and a is a constant.

  19. Find the selling price if 1200 units are sold and a = 60.

  20. Find the selling price if 1860 units are sold and a = 232.

5.8  Additional Equations Review (Optional)

  Solving equations is one of the most important topics in a beginning algebra course. In this section, you are provided with review exercises to help maintain the skills and understanding related to solving equations. The techniques discussed in previous sectionsare used in solving these equations, and some of the equations have fractions for solutions. 

Examples

  1. Solve the following equations. 

   5x+3=7  Write the equation.

   5x=4  Add -3 to both sides.

   x=4/5  Divide both sides by 5.

Check:

   5*(4/5)+3=7

   4+3=7

  2. 2x^2+9x+9=0  Write the equation.

   (2x+3)(x+3)=0  Factor.

   2x+3=0  or  x+3=0

   2x=-3      x=-3

   x=-(3/2)

Checking both solutions:

   2(-3/2)^2+9(-3/2)+9=0  

   2(9/4)-27/2+9=0

   9/2-27/2+9=0

   0=0

    

   2(-3)^2+9(-3)+9=0

   18-27+6=0

   0=0

Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.