Vertical & Horizontal Lines and Obliques

7.3  Vertical and Horizontal Straight Lines

There are two problems that relate equations and graphs, namely,
1. sketching the graph of a given equation.
2. determining an equation for a given graph.
  By sketching the graph of a given equation, we mean plotting some of the solution pairs and estimating the others with some sort of curve. In determining an equation for a given curve, we first assume that the curve is specified geometrically in some way. For example, it may be the line on points P: (2,2) and Q: (-3, 7) or it might be the circle with center (-1,1) and radius 5/2. Thus, an equation for the curve is an equation whose graph is that given curve. As we shall see later in this chapter, an equation for the line above is y+x-4=0, while one for the circle is (x+1)^2+(y-1)^2=25/4.
Naturally each of these problems in its full generality is difficult. Consequently we will consider graphing and finding equations only for special classes of equations and curves.
The simplest curves in the plane are the straight lines. In particular, let {iota} be a line that is parallel to the Y axis. See Figure 4. If {iota} intersects the X axis at the point at directed distance a from the origin O, then, by the rule for assigning first coordinates to points, the points on {iota} are exactly the ones whose first coordinate is a. Thus an equation for {iota} is

x = a

On the other hand, to go from the algebraic equation

x = a

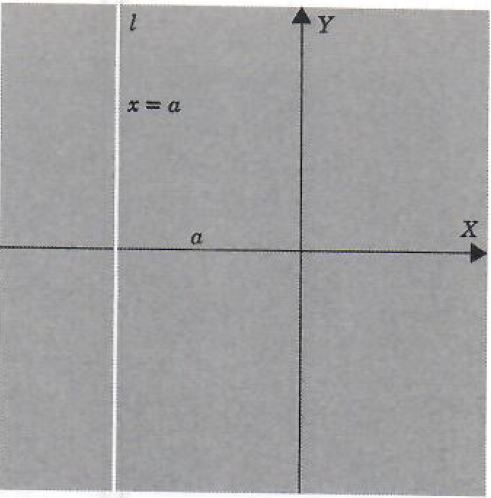
FIGURE 4.

to its graph, we see that its solution set is precisely those points whose first coordinate is the number a. The graph of this set is, by the rule for prescribing first coordinates to points, exactly those points on the vertical line which intersects X at the directed distance a from O.
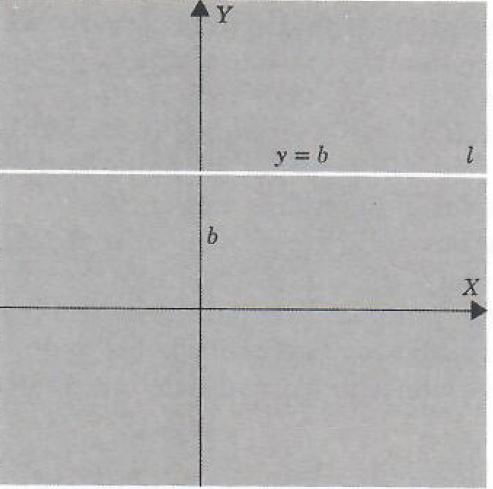
  Similarly, We can see that every horizontal line has an equation of the form
y=b
and every equation of this form has a horizontal line as its graph. Here b is the directed distance from the origin to the point of intersection of the horizontal line with the Y axis.

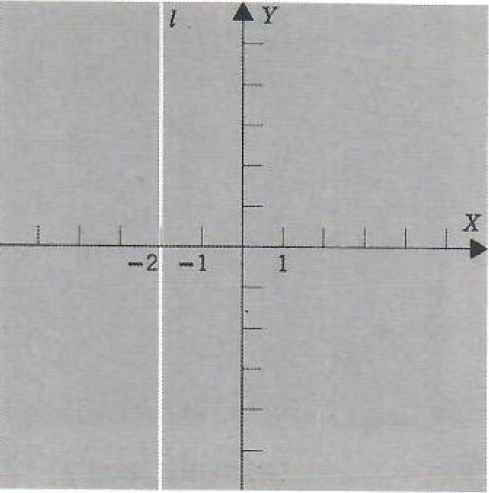
Example 1.  Graph x=-2

From the above investigation, this is the vertical line {iota} that is -2 units
from O.

Example 2.  Find an equation of the horizontal line h which goes through the point (-7, 4).

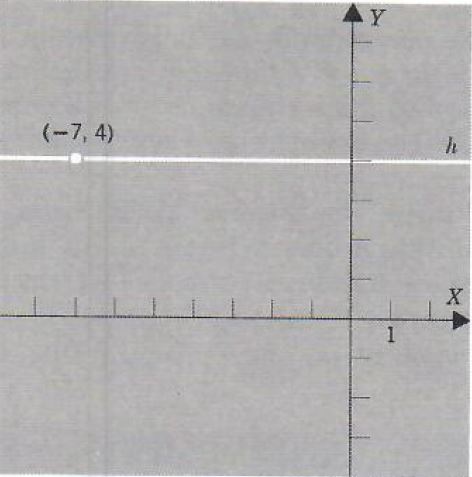
  Since the line is horizontal it has an equation of the form y=b. Since (-7,4) is on h,b=4 and hence the equation is

  y=4

7.4 Oblique Lines

  Let {iota} be a line in the XY plane. In the last section we established the correspondence between vertical lines and equations of the form x=a, and the correspondence between horizontal lines and equations of the form y=b. Lines that are inclined to both axes, called oblique lines, also have equations of a characteristic form. The concept that is used to connect lines with equations is that of slope of a line.
In the XY plane the distance on horizontal and vertical lines is directed according to the direction on the X axis and Y axis, respectively. We denote the directed distance from A to B by AB. It is easy to see as shown in Figure 5 that if A: (x_1,b)and B: (x_2,b) then AB=x_2-x_1. If C:(a,y_1) and D: (a,y_2), then CD=y_2-y_1.

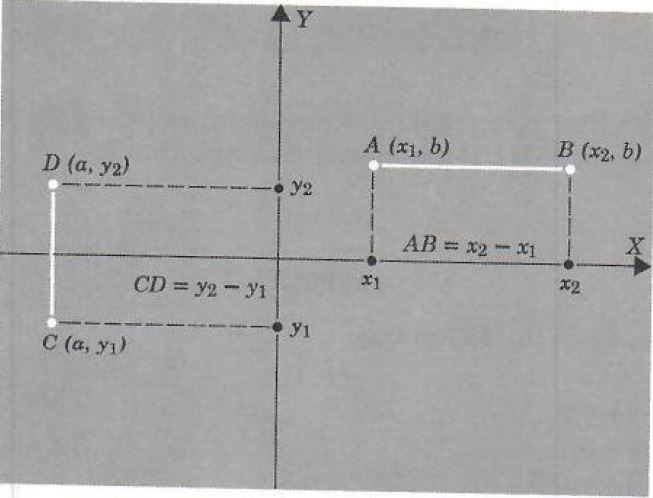
  FIGURE 5.

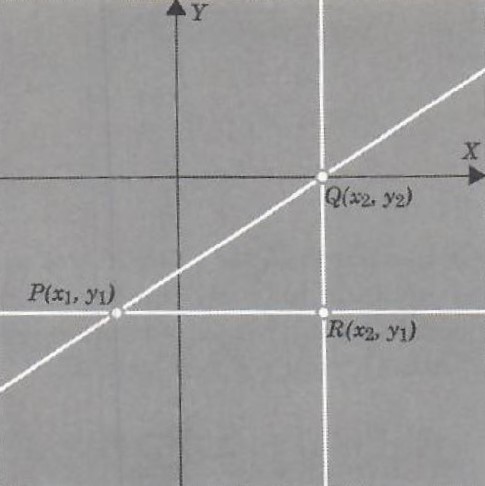
  n Figure 6 we consider a line l that is oblique: Let P and Q be points on {iota} and let R be the point of intersection of the horizontal line on P with the vertical line on Q. We measure the inclination of line {iota} and the X axis by the following ratio.

(1)  m=(RQ)/(PR)

This ratio is called the slope of {iota}. In analytic geometry, two properties of the slope of a line are derived. These properties are
S_1: If {iota} is a line, then the slope m is the same for all choices of pairs of points P and Q on {iota}.

S_2: If P is a point and m is any real number, then there is exactly one line through P with slope m.
The slope of line {iota} can be computed from the coordinates of the two
points P: (x_1,y_1) an Q:(x_2,y_2) on {iota}. See Figure 6. In fact,

and  RQ=y_2-y_1

so    PR=x_2-x_1

(2)   m=(y_2-y_1)/(x_2-x_1)

Example 1.  Let {iota} be the line P:(-1,2) and Q:(3,5). Find the slope of {iota}.

  From(2)  m=(5-2)/(3-(-1))

            =3/4

  Observe that the order in which we use the points is immaterial
since

        (y_1-y_2)/(x_1-x_2)=(y_2-y_1)/(x_2-x_1)

  In Example 1 we could have computed m just as easily by using (3,5) and (-1,2).

        m=(2-5)/(-1-3)

          =-3/-4

          =3/4

  Let the line {iota} pass through the point P: (x_1,y_1) and have slope m. We now derive an equation for {iota}. By the two properties of the slope of a line, another point Q: (x, y) is on {iota} if and only if its coordinates satisfy equation (2). Thus Q is on {iota} if and only if

             (y-y_1)/(x-x_1)=m

Multiplying by x-x_1 we obtain

(3)        y-y_1=m(x-x_1)

Even the coordinates of P, namely, (x_1,y_1), satisfy this equation. Thus (3) is an equation for {iota}. Because it is computed in terms of the slope m and the coordinates (x_1,y_1) of a given point, it is called the point-slope form of the equation for {iota}.

Example 2. 

Let {iota} have slope m = -2 and pass through the point (4,1). Compute the point-slope form of the equation for {iota} and simplify From equation (3) we obtain the point-slope form. 

          y-(-1)=-2(x-4)

Simplifying we obtain

          y+1=-2x+8

          y=-2x+7

  An important special case of the point-slope equation for a line is that in which the given point is the intersection of {iota} with the Y axis. This point is called the Y intercept. The Y intercept has coordinates (0, b) for some real number b. Sometimes just b is referred to as the Y intercept. If {iota} has slope m and Y intercept b, equation (3) becomes

          y-b=m(x-0)

which simplifies to

(4)        y=mx+b

  In the right-hand side of (4) the coefficient m of x is the slope of the line while the constant term b is the Y intercept. This form of the equation for {iota} is called the slope-intercept form. Note that the final equation in Example 2 is in slope-intercept form.

Example 3. 

Obtain the slope-intersect form of the equation for the line {iota} having slope 1/2 and Y intercept 3.
Substituting into (4) we obtain

          y=1/2x+3

Consider an equation of the form (4). From the discussion preceding (4), we know that the equation for the line having slope m and Y intercept b is y=mx+b. Thus the graph of (4) is this line. This simple observation allows quick graphing of all such equations, since any two points on the graph determine the remaining ones.

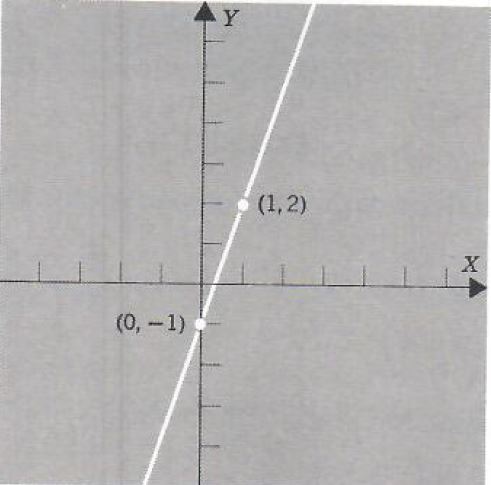
Example 4.  Graph y=3x-1.

Since this equation is of form (4) we know its graph is a straight line. In fact, the Y intercept of this line is (0,-1). If x=1, then

          y=3(1)-1

          =2

so that (1, 2) is another point on the line. Graphing we obtain

Example 5.

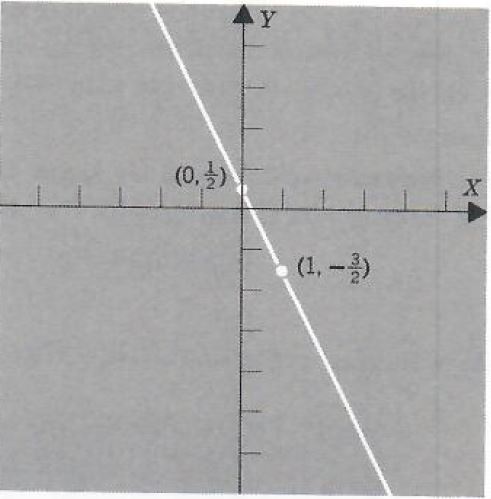
  Find the slope, Y intercept, and draw the graph of 2y+4x=1. This equation is not in the form given in formula (4); hence, we must transform it to an equivalent equation in that form.

          2y+4x=1

          2y=-4x+1

          y=-2x+1/2

Thus the graph of the original equation is the straight line having

slope -2 and Y intercept 1/2. If x=l, then

          y=-2(1)+1/2

          =-(3/2)

Thus (1, -3/2) is another point on the line

you can see positive slope or negative slope depending upon the equation of line using our graph generator. Please click on "Solve Similar" to generate various graphs.