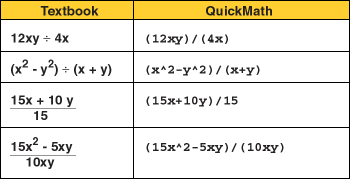
Here are some examples of typical expressions involving division. This table shows you what they would look like in a textbook and how they would need to be entered for QuickMath.