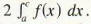The integrate command will calculate definite and indefinite integrals.
In order to use the basic integrate command to find an indefinite integral, simply enter the expression you wish to integrate, enter the variable to integrate with respect to and click the Integrate button. If you wish to find the definite integral between two limits, a and b say, enter x,a,b in the variables text area.
The advanced integrate command allows you to calculate multiple integrals. Simply enter each variable you wish to integrate with respect to (with limits as described above if required) on a separate line in the variables text area.
Examples
Here are some examples illustrating the types of expressions you can use the integrate command on and the results which QuickMath will return.
Basic integrate command
| Expression | Variable(s) | Result |
| x | x |
2 x -- 2 |
| x^3 | x |
4 x -- 4 |
| 5 x^3 - 7 x^2 + 2 x - 1 | x |
3 4
2 7 x 5 x
-x + x - ---- + ----
3 4
|
| 5 x^3 - 7 x^2 + 2 x - 1 | x,3,5 |
1396 ---- 3 |
| sin(t) | t | -cos(t) |
| sin(t) cos(t) | t |
2
-cos(t)
--------
2
|
| ln(x)y + 3x^2y^3 | x |
3 3
-(x y) + x y + x y log(x)
|
Advanced integrate command
| Expression | Variable(s) | Result |
| 6 x^3 y^2 + 3 x y^4 |
x y |
4 3 2 5 x y 3 x y ----- + ------- 2 10 |
| 6 x^3 y^2 + 3 x y^4 |
x,2,3 y,5,6 |
9934 |
The Integral as an Area
The definite integral, introduced in this section, and the derivative are probably the two fundamental concepts in calculus. We shall introduce the definite integral in terms of the geometrical notion of "area under a curve." The familiar geometrical concept of area provides an intuitive way to approach the integral. However, the definite integral has many other applications. In the next chapter, we shall see applications to business, science, and probability and statistics. The tie-in between the antiderivative and the integral will become more apparent in the next section.
As a preliminary word on notation, closed intervals of the form a <= x <= b are frequently referred to by means of the standard notation [a, b]. Then, in defining the integral as the "area under a curve," the curve we consider is the graph of a function and the area is the one "between" the graph on a closed interval [a, b] and the horizontal axis. Strictly speaking, it is the area bounded by the graph, the horizontal axis. and the lines x = a and x = b. To make sure there is such an area, we want the function to satisfy the following conditions.
- The graph is the graph of a continuous function, or it can be constructed by "pasting together" graphs of functions that have only "jump" discontinuities (see Figure 1). Such functions are called piecewise continuous.
- The graph should be above or touch the horizontal axis: that is, f(x) >= 0 for x in [a, b]. Our reasoning is that if we allowed the graph to dip below the horizontal axis, then the function values would be negative and the part below the axis would be subtracted from the area. We will pursue this later. Keep in mind that an area is a nonnegative real number.
We are about to introduce what may seem to be rather curious notation. (The objects we are now defining will ultimately have more application than area, and we need a sufficiently general notation.)
Let/be a function satisfying Conditions 1 and 2. For any x in [a, b ], the area under the graph off from a to x (see Figure 2) is denoted by
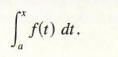
This new symbol is called the definite integral of f from a to x, or, more briefly, the integral of f from a to x. Thus,
Warning! Although the notations for both the integral and the antiderivative include the integration symbol, they should not be confused; the underlying concepts the represent are quite distinct. We shall see later an amazing relationship between these concepts.
Note that the integral depends on x (as well as a and f, of course); thus, to keep the bookkeeping straight, the function f will be given in terms of some variable other than x such as t , for example, in the above definition and it will be convenient to think of the horizontal axis as, in this case, a t-axis (see Figure 2). In terms of this new notation:

Example 1 Interpret 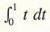 as an area and compute its value.
as an area and compute its value.
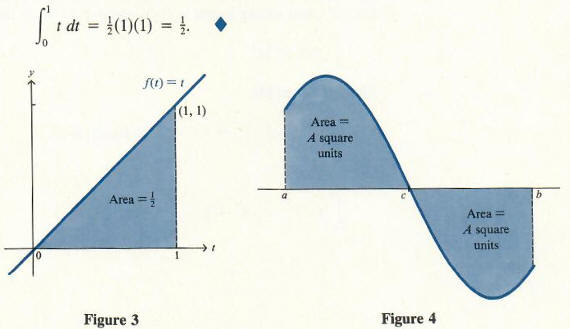
This integral is the area under the graph of f(t) = r from t = 0 to t = 1. As shown in Figure 3, this is the area of a triangle whose base and height are each 1, and since area = 1/2*(base)*(height), we see that:
For functions satisfying Conditions 1 and 2, the integral may be interpreted as an area. For an arbitrary continuous or piecewise continuous function (arbitrary in the sense that the function may be positive for some values and negative or zero for others) a useful interpretation of the integral is as a "signed" area in the following sense: whenever the graph of f is above the x-axis, the integral of f is the area under the graph of f, interpreted in the usual geometrical way as a positive number, but when the graph of f is below the x-axis, the negative of the area is used when integrating f. Another way to think of this is the following:

integration of f adds areas of regions that lie above the x-axis and subtracts areas of regions that lie below the x-axis.
For example, suppose f is the function graphed in Figure 4. The area under the graph of f from a to c is equal to the area under the graph from c to b; suppose each equals A square units. Since the graph of f lies below the x-axis from c to b , this area is subtracted when we evaluate the integral, and hence
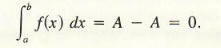
Notice that the area under the curve (that is, number of square units in the region) is 2A square units and hence the area is given by