Description

The inverse command in the matrices section of QuickMath allows you to find the inverse of any non-singular, square matrix.

A non-singular matrix is one which has a non-zero determinant, whilst a square matrix is one which has the same number of rows and columns.

The inverse of a square matrix A is another matrix B of the same size such that

A B = B A = I

To use the inverse command, simply go to the inverse page, type in your matrix and hit the "Inverse" button. Your question will be automatically answered by computer and the reply will be shown in your browser within a few seconds. The answer will be given in two forms : a 'natural' form, which mimics the row and column layout normally used for matrices, and an 'input' form, which is the form required for the entry of matrices into QuickMath. The input form of a solution can be copied and pasted into a matrix input field, so you can use the result from one calculation in another calculation without having to re-type it.

Examples

     d                   b
------------      -(------------)
-(b c) + a d        -(b c) + a d

       c               a
-(------------)   ------------
  -(b c) + a d    -(b c) + a d 

-2     1

3        1
-      -(-)
2        2 

157               47      3
---             -(--)   -(-)
12      -7        12      2

  44            13      5
-(--)           --      -
  3     8       3       3

65                19      1
--              -(--)   -(-)
12      -3        12      2

11                3       2
--              -(-)    -(-)
2       -3        2       3 

Finding the Inverse of a Matrix

FINDING THE INVERSE OF A 2 X 2 MATRIX

Given

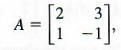
find A^-1.

Find A^-1 by going through the following steps.

Step 1 Form the augmented matrix [A|I].

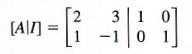
Perform row operations on [A|l] until a new matrix of the form [I|B] is obtained, as follows.

Step 2 Interchanging the first and second rows gives a l in the upper left-hand corner.

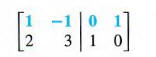
Step 3 Multiplying the elements of the first row by -2 and adding the results to the second row gives a 0 in the lower left-hand corner.

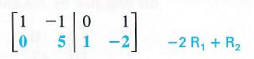
Step 4 Multiplying the elements of the second row by 1/5 gives a 1 for the second element in that row.

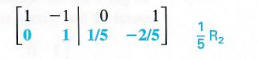
Step 5 Replacing the first row by the sum of the first row and the second row gives a 0 as the second element in the first row.

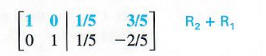
This last matrix is in the form [I|B], where

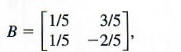
which should equal A^-1. To check, multiply B and A. The result should be I.

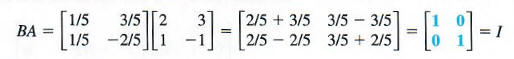
Verify that AB also equals I, so that

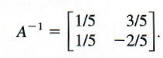
FINDING THE INVERSE OF A 3 X 3 MATRIX

find A^-1

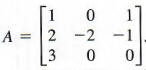
Use row transformations as follows.

Step 1 Write the augmented matrix [A|I].

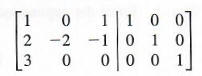
Step 2 Since l is already in the upper left-hand comer as desired, begin by using the row transformation that will result in a 0 for the first element in the second row. Multiply the elements of the first row by -2, and add the results to the second row.

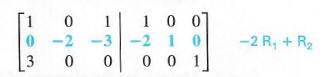
Step 3 To get 0 for the first element in the third row, multiply the elements of the first row by - 3 and add to the third row

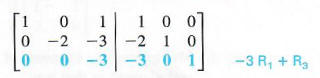
Step 4 To get 1 for the second element in the second row, multiply the elements of the second row by - 1/2.

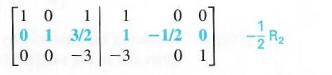
Step 5 To get 1 for the third element in the third row, multiply the elements of the third row by -1/3.

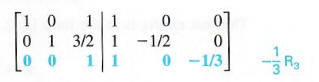
Step 6 To get 0 for the third element in the first row, multiply the elements of the third row by - I and add to the first row

Step 7 to get 0 for the third element in the second row, multiply the elements of the third row by -3/2 and add to the second row.

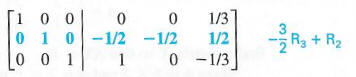
The last transformation shows that the inverse is

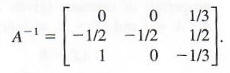
Confirm this by forming the products A^-1 *A and A*A^-1, each of which should equal the matrix I.

As illustrated by the examples, the most efficient order of steps is to make the changes column by column from left to right, so that for each column the required 1 is the result of the first change. Next, perform the steps that obtain the zeros in that column. Then proceed to another column. Since it is tedious to find an inverse with paper and pencil, these same steps can be adapted for a computer program. A computer can produce the inverse of a large matrix, even a 100 X 100 matrix, in a mili-second.

IDENTIFYING A MATRIX WITH NO INVERSE

Example 5

Find A^-1 given

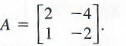
Using row transformations to change the first column of the augmented matrix

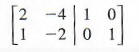
results in the following matrices:

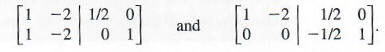
(We multiplied the elements in row one by 1/2 in the first step.) At this point, the matrix should be changed so that the second-row, second-column element will be 1. Since that element is now 0, there is no way to complete the desired trans formation, so A^-1 does not exist for this matrix A. What is wrong? Just as there is no multiplicative inverse for the real number 0, not every matrix has a multiplicative inverse. Matrix A is an example of such a matrix.

MATRIX EQUATIONS

Matrix equations are solved in much the same way as real-number equations. Properties of matrices are used, together with a multiplication property of equality for matrices that allows both sides of a matrix equation to be multiplied by any appropriate matrix. The next example shows how to solve a matrix equation.

Example 6

Given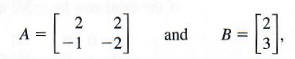


find a matrix X so that AX = B.

Since A is 2 X 2 and B is 2 X l, matrix X will be a 2 X 1 matrix, like B. The matrix equation AX = B can be solved as a linear equation is solved, with the properties of matrices  and the facts that if A^-1 exists, A^-1A = I and IX= X, as follows.

To find X, first find A^-1. Verify that

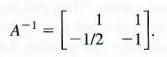
As shown above,

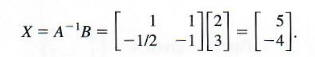
Check:

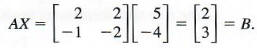
CAUTION In using the multiplication property of equality for matrices, be careful to multiply on the left on both sides of the equation. Unlike multiplication of real numbers, multiplication of matrices is not commutative.

The result from Example 6 can be used to solve linear systems by first writing the system as a matrix equation AX = B, where X is a matrix of the variables of the system. Then the solution is X = A^-1 B.