Multiplication and Division of Radical Expressions

10.4  Multiplication of Radical Expressions

  Multiplication of radical expressions is possible using the rule

    root(n,a)root(n,b)=root(n,ab) for a,b∈R,a>0,b>0

EXAMPLE  1. root(2)root(3)=root(2*3)=root(6)

        2. root(6)root(33)=root(6*33)

               =root(2*3*3*11)=3root(22)

       3. 2root(x)root(xy)=2root(x*xy)=2root(x^2y)=2xroot(y)

        4. 3root(3,2)*2root(3,5)=(3*2)root(3,2*5)=6root(3,10)

        5. root(3,4)root(3,6)=root(3,24)=root(3,2^3*3)=2root(3,3)

Note    The final radical must be in standard form.

  To multiply one radical by a radical expression of more than one term, we use the distributive law: a(b+c)=ab+ac.

EXAMPLE  Multiply 3root(2)(5root(6)-2root(10)) and simplify.

Solution   3root(2)(5root(6)-2root(10))

      =3root(2)*5root(6)-3root(2)*2root(10)

      =root(12)-6root(20)

      =30root(3)-12root(5)

EXAMPLE  Multiply 2root(3xy)(4root(x)-3root(y)) and simplify.

Solution   2root(3xy)(4root(x)-3root(y))

      =8root(3x^2y)-6root(3xy^2)

      =8xroot(3y)-6yroot(3x)

  To multiply two radical expressions, each with more than one term, follow the same arrangement as in multiplying polynomials.

EXAMPLE  Multiply (2root(3)-4root(2)) by (3root(3)+root(2)) and simplify.

Solution   

       

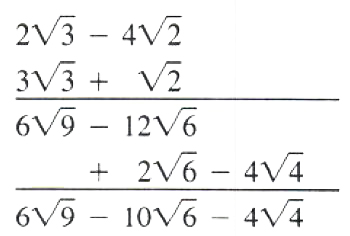
      Hence (2root(3)-4root(2))(3root(3)+root(2))

      =6root(9)-10root(6)-4root(4)

      =18-10root(6)-8

      =10-10root(6)

EXAMPLE  Multiply root(3x)-root(2y) by 5root(3x)+2root(2y) and simplify.

Solution   

      

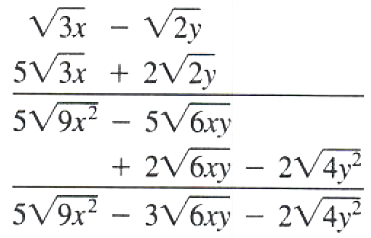
      Hence (root(3x)-root(2y))(5root(3x)+2root(2y))

      =5root(9x^2)-3root(6xy)-2root(4y^2)

      =15x-3root(xy)-4y

      =15x-4y-3root(6xy)

EXAMPLE  Expand (root(x+3)+root(x-2))^2 and simplify.

Solution   

      

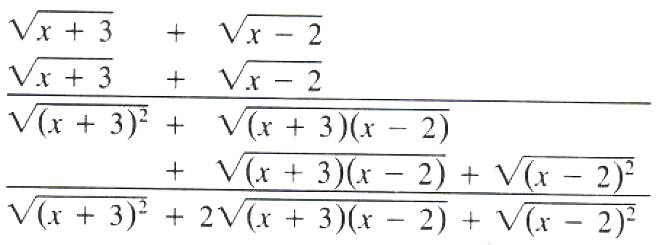
      Hence (root(x+3)+root(x-2))^2

      =root((x+3))^2+2root((x+3)(x-2))+root((x-2))^2

      =x+3+2root(x^2+x-6)+x-2

      =2x+1+2root(x^2+x-6

Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.

Note     (root(a)+root(b))^2!=a+b

      (root(a)+root(b))^2=(root(a)+root(b))(root(a)+root(b))=a+2root(ab)+b  When the radicals have different indices, we apply the rule root(n,a^m)=root(nk,a^mk)to make the indices the same as their LCM and then apply root(n,a)root(n,b)=root(n,ab).

EXAMPLES  1. root(3)root(3,3^2)=root(6,3^3)root(6,3^7)=root(6,3^7)=3root(6,3)

        2. root(3,a^2)root(4,a^3)=root(12,a^8)root(12,a^9)=root(12,a^17)=aroot(12,a^5)

10.5  Division of Radical Expressions

THEOREM  When a,b∈R,a>0,b>0, and n∈N, then root(n,a)/root(n,b)=root(n,a/b).

Proof    root(n,a)/root(n,b)=a^(1/n)/b^(1/n)=(a/b)^(1/n)=root(n,a/b)

  Radical expressions can be divided according to the above theorem only when the radical indices are the same. For different radical indices, the preliminary step to make them the same must be carried out.

EXAMPLES  1. root(15)/root(5)=root(15/5)=root(3)

        2. root(x^3y^5)/root(x^2y)=root((x^3y^5)/(x^2y))=root(xy^4)=y^2root(x)

   Sometimes the numerator of a fractional radicand is not an exact multiple of the denominator, for example root(3/2) To simplify such a radical, multiply both numerator and denominator of the radicand by the smallest number that will make the denominator a perfect root.

Note    The denominator is a perfect root if the exponent of each factor is an integral multiple of the radical index.

  To simplify root(3/2)multiply the numerator and denominator of the radicand by 2.

      root(3/2)=root((3*2)/(2*2)=root(6)/2 or 1/2root(6)

  It is easier to manipulate 1/2root(6) than root(3/2).

Remark  When the radical expression is of the form a/(b√c), multiply the numerator and the denominator by root(c).

      2/root(3)=2/root(3)=root(3)/root(3)=(2root(3))/3

      4/root(50)=4/(5root(2))=4/(5root(2))=root(2)/root(2)=(root(2))/10=(2root(2))/5

EXAMPLE  Divide root(15) by root(21)and put in standard form.

 Solution   root(15)/root(21)=root(15/21)=root(5/7)=root((5*7)/(7*7))=1/7root(35)

EXAMPLE  Divide root(3xy) by root(4a^3b)and put in standard form.

 Solution   root(3xy)/root(4a^3b)=root((3xy)/(2^2a^3b))=root((3xy)/(2^2a^4b)*(ab)/(ab))

        =root((3xyab)/(2^2a^4b^2))

        =1/(2a^2b)root(3xyab)

EXAMPLE  Put root((3a^2b^3)/(20xy^5))in standard form.

 Solution   root((3a^2b^3)/(20xy^5))=root((3a^2b^3)/(2^2*5xy^5)*(5xy)/(5xy)

              =root((15a^2b^3xy)/(2^2*5^2x^2y^6)

              =(ab)/(10xy^3)root(15bxy)

EXAMPLE  Divide root(3,3) by root(3,20)and put in standard form.

Solution   root(3,3)/root(3,20)=root(3,3/(2^2*5))=root(3,3/(2^2*5)*(2*5^2)/(2*5^2)

                    =root(3,(3*2*5^2)/(2^3*5^3))

                    =1/10root(3,150)

EXAMPLE  Put root(3,(81x^6y^7)/(8a^8b^10)in standard form.

Solution   root(3,(81x^6y^7)/(8a^8b^10)=root(3,(3^4x^6y^7)/(2^3a^8b^10))=root(3,(3^4x^6y^7)/(2^3a^8b^10)*(ab^2)/(ab^2))

        =root(3,(3^4x^6y^7ab^2)/(2^3a^9b^12))=(3x^2y^2)/(2a^3b^4)root(3,3yab^2)

  The definition of addition of fractions, (a+b)/c=a/c+b/c, is used to divide a radical expression with more than one term by a one-term radical.

EXAMPLE  Divide and simplify (3root(6)-6root(10))/(3root(2)).

Solution   (3root(6)-6root(10))/(3root(2))

      =(3root(6))/(3root(2))-(6root(10))/(3root(2))

      =root(6)/root(2)-(2root(10))/root(2)

      =root(6/2)-2/1root(10/2)

      =root(3)-2root(5)

EXAMPLE  Divide and simplify (root(7x)-root(2y))/root(14xy).

Solution   (root(7x)-root(2y))/root(14xy)

      =root(7x)/root(14xy)-root(2y)/root(14xy)

      =root((7x)/(14xy))-root((2y)/(14xy))

      =root(1/(2y))-root(1/(7x))

      =root((2y)/(2^2y^2))-root((7x)/(7^2x^2))

      =1/(2y)root(2y)-1/(7x)root(7x)

  When we multiply the radical expressions (root(a)+root(b)) and (root(a)-root(b)), we have get the rational expression (a-b). Each of the expressions (root(a)+root(b)) and (root(a)-root(b)) is called a rationalizing factor of other.

EXAMPLES  1. root(2)-root(3)is a rationalizing factor of root(2)+root(3).

         2. 2+3root(2)is a rationalizing factor of 2-3root(2).

  To facilitate the manipulation with a radical expression such as (root(2)+root(3))/(2root(2)+root(3)), we change the fraction to an equivalent one with a rational denominator. This can be accomplished by multiplying both numerator and denominator by the rationalizing factor of the denominator, 2root(2)-root(3).

  This operation is called rationalizing the denominator

EXAMPLE  Rationalize the denominator of root(2)/(2-root(3)).

Solution   root(2)/(2-root(3))

      =(root(2)(2+root(3)))/((2-root(3))(2+root(3))

      =(2root(2)+root(6))/(4-3)=2root(2)+root(6)

EXAMPLE  Rationalize the denominator of (root(2)+root(3))/(2root(2)+root(3)).

Solution   (root(2)+root(3))/(2root(2)+root(3))

      =((root(2)+root(3))(2root(2)-root(3)))/((2root(2)+root(3))(2root(2)-root(3))

      =(1+root(6))/(8-3)

      =1/5(1+root(6))

Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.