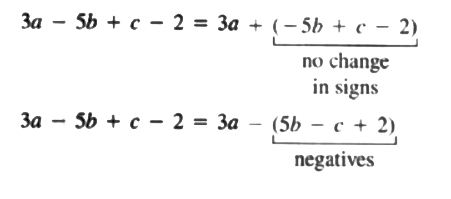Example: 2x-1=y,2y+3=x
To see your tutorial, please scroll down
Multiplication of Polynomials
Multiplication of Polynomials
Definition and Notation
The product of two natural numbers, 3 and 4, is defined by
3 x 4 = 4 + 4 + 4 three terms of 4
Similarly 5a = 5 * a = a + a + a + a + a five terms of a
4ab = ab + ab + ab + ab four terms of ab
ab=a x b = b + b +....+ b a terms of b
The following are some of the laws from
1. The commutative law of multiplication: ab = ba
2. The associative law of multiplication: a(bc) = (ab)c
3. The distributive law of multiplication: a(b + c) = (b + c)a
=ab + ac
4. Multiplication of signed numbers:
+a)(+b) = +ab; (+a)(-b) = -ab
(-a)(+b) = -ab; (-a)(-b) = +ab
When we have 2 * 2 * 2 * 2. that is, four factors of 2, the notation 2^4 is used, which reads. “two to the power four," or “two to the fourth power."
Similarly, a * a * a * a * a = a^5 means five factors of a. The a is called the base, and the 5 is called the exponent. When there is no exponent, as in x, we always mean x to the power 1.
DEFINITION
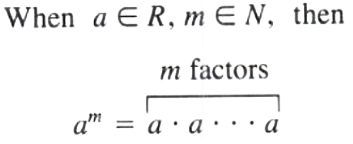
Note the difference between
(-2^4) = (-2)(-2)(-2)(-2) = +16
and -2^4 = -(2^4) = -(2 * 2 *2 *2) = -16
Note also 2a^3 = 2(a*a*a)
While (2a)^3 = (2a)(2a)(2a)
=(2*2*2)(a*a*a)
=2^3a^3 = 8a^3
Remark a , a^2 , a^3,.... are not like terms.
EXAMPLES 1. 7a*a*a*a = 7a^4
2. -(-3)(-3)(-3)(-3) = -(-3)^4
3. (x - 1)^3 = (x - 1)(x -1)(x - 1)
4. -2^2*3^3 = -(2*2)*(3*3*3) = -4*27 = -108
5. 2^2 + 2^3 = 2*2 + 2*2*2 = 4 + 8 = 12
6. 2^3 - 2 = 2*2*2 -2=8 - 2 = 6
Multiplication of Monomials
We will discuss the multiplication of monomials, then the multiplication of a monomial and a polynomial, and finally the multiplication of two polynomials.
From the definition of exponents we have
a^3*a^5 = (a*a*a)(a*a*a*a*a)
=a*a*a*a*a*a*a*a
=a^8
=a^(3+5)
THEOREM 1
Proof
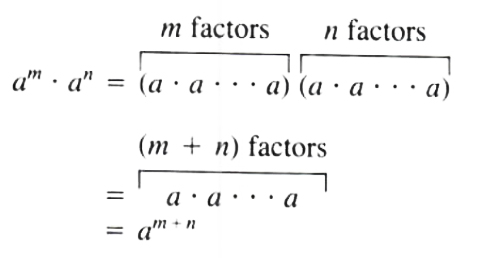
EXAMPLES 1. 2^3 * 2^5 = 2^(3+5) = 2^8
2. a^2 * a^4 = a^(2+4) = a^6
3. -2^4 * 2^3 = -2^(4+3) = -2^7
4. -3x^3*x^2 = -3x^(3+2) = -3x^5
5. x^5*x = x^(5+1) = x^6
6. (a + 1)^2*(a + 1)^3 = (a + 1)^(2+3) = (a + 1)^5
Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
Remark 2^3*2^7 = 2^(3+7) = 2^10 , and not 4^10
Remark 2^4*3^5 = 2^4*3^5 , to find the product, multiply 2^4 =16 by 3^5 =243 ; that is 2^4*3^5 = (16)(243) = 3888
Since the commutative and associative laws for multiplication hold for numbers, specific or general. we have
EXAMPLES 1. (2ab^2)(3a^4bc^2)= (2*3)(a^1*a^4)(b^2*b^1)(c^2)
= 6a^5b^3c^2
2. -3b^2c^3)(8ab^3c) = (-3*8)(b^2*b^3)(c^3*c)(a)
=-24b^5c^4a
3. -3^2xy^2)(-5x^2y^3) = (-9xy^2)(-5x^2y^3)
=(-9)(-5)(x*x^2)(y^2*y^3)=45x^3y^5
Let's see how our Polynomial solver simplifies this and similar problems step-by-step. Click on "Solve Similar" button to see more examples.
From the definition of exponents we have
(a^2)^3 = (a^2)(a^2)(a^2)
=(a^2*a^2)(a^2)
=a^(2+2)*a^2
=a^(2+2+2)
=a^(3*2) = a^(2*3)
=a^6
THEOREM 2
Proof
EXAMPLES 1. (3^2)^4 = 3^(2*4) = 3^8
2. (a^3)^5 = a^(3*5) = a^15
3. (-3^2)^3 = -3^(2*3) = -3^6
4. (-a^3)^2 = a^(3*2) = a^6
Note 2^3*2^4 = 2^(3+4)=2^7, While (2^3)^4 = 2^(3*4)=2^12
From the definition of exponents we have
6^4 = (2*3)^4 = (2*3)(2*3)(2*3)(2*3)
= (2*2*2*2)(3*3*3*3)
=2^4*3^4
THEOREM 3
Proof
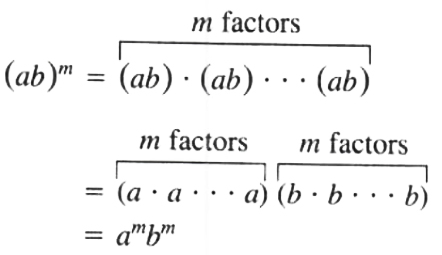
Note a and b are factors. If a=3, b=x, and m=5,(3x)^5=3^5x^5
Do not forget to raise the number 3 to the power 5
Applying Theorem 3 repeatedly, we obtain
(abcd)^m=[(ab)(cd)]^m
=(ab)^m(cd)^m
=a^mb^mc^md^m
Remark 21^2 = (3*7)^2 = 3^2*7^2 = 9 x49 = 441
Remark The quantity 
(5 + 3)^2 = (8)^2 = 64, but 5^2 + 3^2 = 25 + 9 = 34
If we consider (a + b) as one quantity, then
(a +b)^5 = (a +b)(a + b)(a + b)(a + b)(a + b)
The method of calculating the product will be explained later
COROLLARY 
(a^m)(b^n)^k = [(a^m)(b^n)]^k
=(a^m)^k(b^n)^k
=a^mkb^nk
EXAMPLE Perform the following multiplication: (2x^2yz^3)(-4x^3y^2)
Solution (2x^2yz^3)(-4x^3y^2) = (2)(-4)(x^2*x^3)(y*y^2)(z^3)
= -8x^5y^3z^3
Let's see how our Polynomial solver simplifies this and similar problems, showing explanations for each step. Click on "Solve Similar" button to see more solved examples.
EXAMPLE Perform the following multiplication: (5a^2b)^3
Solution (5a^2b)^3 = (5)^3(a^2)^3(b)^3 = 5^3a^6b^3 = 125a^6b^3
EXAMPLE Perform the following multiplication: -2^2a^3(ab^3)^2
Solution -2^2a^3(ab^3)^2 = -4a^3(a^2b^6) = -4(a^3*a^2)(b^6) = -4a^5b^6
EXAMPLES Perform the following multiplication: (3x^2y)^2(2xy^3)^3
Solution (3x^2y)^2(2xy^3)^3 = (3^2x^4y^2)(2^3x^3y^9) = (3^2*2^3)(x^4*x^3)(y^2*y^9)
=(9*8)x^7y^11 = 72x^7y^11
Remark Perform the outside exponents first
EXAMPLE Perform the following multiplication:
(-2ab^2)^2(-3a^2b)^3(-bc^2)^4
Solution (-2ab^2)^2(-3a^2b)^3(-bc^2)^4 = (-2)^2a^2b^2*(-3)^3a^6b^3*(-1)^4b^4c^8
=(-2)^2(-3)^3(-1)^4(a^2*a^6)(b^4*b^3*b^4)(c^8)
=(4)(-27)(+1)a^8b^11c^8
=-108a^8b^11c^8
EXAMPLE Perform the indicated operations and simplify:
(2ab)^4(-a^3b)^2 - (-3a^2)^3(a^2b^3)^2
Solution (2ab)^4(-a^3b)^2 - (-3a^2)^3(a^2b^3)^2 = (16a^4b^4)(a^6b^2) - (-27a^6)(a^4b^6)
=16a^10b^6 + 27a^10b^6
=43a^10b^6
Let's see how our Polynomial calculator explains all simplification steps
Note: To evaluate expressions involving exponents. first replace each letter by its indicated specific value. Use grouping symbols where necessary so as not to confuse operation signs with number signs.
Evaluate -a^2b^3, give that a = -3 and b = 2
Solution -a^2b^3 = -(-3)^2(2)^3 = -(9)(8) = -72
EXAMPLE Evaluate the expression b^2 - a^2(c^3 - b^3), give that a = -2 , b = 3, and c = -1
Solution b^2 -a^2(c^3 - b^3) = (3)^2 - (-2)^2[((-1)^3 - (3)^3
=9 - (+4)[(-1) - (27)
=9 - 4(-1 -27)
=9 - 4(-28)
=9 + 112 = 121
Multiplication of a Polynomial by a Monomial
The extended distributive law of multiplication
is used to multiply a monomial by a polynomial
EXAMPLE Multiply 3x^2 + x - 2 by x
Solution x(3x^2 + x - 2) = x(3x^2) + x(x) + x(-2)
=3x^2 + x^2 - 2x
EXAMPLE Multiply x^2 - x + 4 by -2x^2
Solution (-2x^2)(x^2 - x + 4) = (-2x^2)(x^2) + (-2x^2)(-x) + (-2x^2)(4)
=-2x^4 + 2x^3 - 8x^2
EXAMPLE Multiply a^2b - 2b^2c + 5c^2a by 3a^2b
Solution 3a^2b(a^2b - 2b^2c + 5c^2a)
=3a^2b(a^2b) + 3a^2b(-2b^2c) + 3a^2b(5c^2a)
=3a^4b^2 - 6a^2b^3c + 15a^3bc^2
EXAMPLE Multiply (3x - 2)/4 - (2x - 1)/6 by 12
Solution 12/1[(3x - 2)/4 - (2x - 1)/6 = 12/1[(3x - 2)/4 - 12/1[(2x - 1)/6
=3(3x - 2) - 2(2x - 1)
=9x - 6 - 4x + 2
=5x - 4
Multiplication of Polynomials
Multiplication of two polynomials is the same as multiplication of a monomial and a polynomial where the first polynomial is considered as one quantity.
To multiply (x + 2) by (x - 3), consider (x + 2) as one quantity and apply the distributive law:
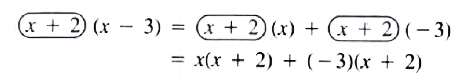
Then reapply the distributive law
=x^2 + 2x - 3x - 6
=x^2 - x - 6
Notice that each term of the second polynomial has been multiplied by each term of the first polynomial.
The same result can be obtained by arranging the polynomials in two rows and multiplying the upper polynomial by each term of the lower polynomial. Arrange like terms of the product in the same column so that addition is easier.+
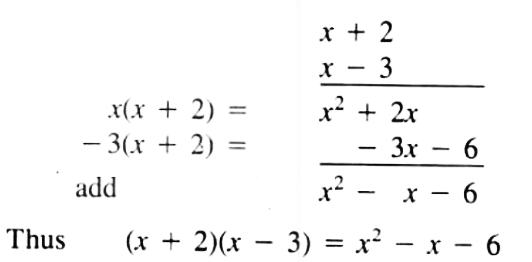
EXAMPLE Multiply (3x - 4)^2
Solution (3x - 4)^2 = (3x - 4)(3x - 4)
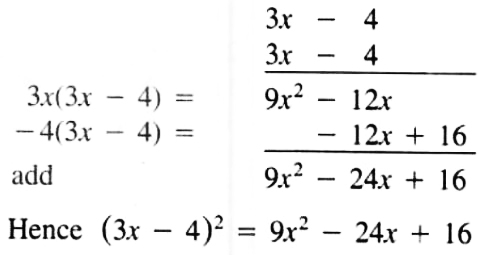
Notes 1. (a + b)^2 = a^2 + 2ab + b^2
2. (a - b)^2 = a^2 - 2ab + b^2
3. (a + b)(a - b) = a^2 - b^2
EXAMPLE Multiply (x^2 - 2x +1) by (2x - 3)
Solution
Therefore (x^2 - 2x + 1)(2x - 3) = 2x^3 - 7x^2 + 8x - 3
EXAMPLE Perform the indicated operations and simplify
(2x - 3)(x + 4) - (x + 2)(x - 6)
Solution (2x - 3)(x + 4) - (x + 2)(x - 6)
=(2x^2 -+5x -12) - (x^2 - 4x - 12)
=2x^2 + 5x - 12 - x^2 + 4x + 12
=x^2 + 9x
Grouping Symbols
Grouping symbols, such as parentheses ( ), braces { }, and brackets [ ], are used to designate, in a simple manner, more than one operation.
When we write the binomial 3a + 5b as (3a + 5b), we are considering the sum of 3a and 5b as one quantity. The expression a - (b + c) means the sum of b and c is to be subtracted from a.
The statement, three times x minus four times the sum of y and z, can be written in algebraic notation as
3x - 4 (y + z)
Removal of the grouping symbols means performing the operations that these symbols indicate. Remove the symbols one at a time, starting with the innermost, following the proper order of operations to be performed.
EXAMPLE Remove the grouping symbols and combine like terms
2x - (5x - 2y) + (x - 6y)
Solution 2x - (5x - 2y) + (x - 6y) = 2x - 5x + 2y + x -6y
=(2x - 5x + x) + (2y - 6y)
=-2x - 4y
Let's see how our polynomial solver simplifies this and similar problems. Clicking on "Solve Similar" button will show more step-by-step solved examples.
EXAMPLE Remove the grouping symbols and combine like terms
7a + 2[2b - 3(3a - 5b)
Solution 7a + 2[2b - 3(3a - 5b) = 7a + 2[2b - 9a +15b
=7a + 4b -18a +30b
=34b -11a
Let's see how our polynomial calculator explains all the steps for this and similar problems. Click on "Solve Similar" button to see more examples solved.
EXAMPLE Remove the grouping symbols and combine like terms
6a - {2b + [3 - (a + b) + (5a - 2)}
Solution 6a - {2b + [3 - (a + b) + (5a - 2)}
=6a - {2b + [3 - a - b + 5a -2]}
=6a - {2b + 3 - a -b +5a -2}
=6a - 2b -3 +a +b -5a +2
=(6a + a - 5a) + (-2b + b) + (-3 +2)
=2a - b -1
Let's see how our polynomial calculator solves this and similar problems. Click on "Solve Similar" button to see more examples.
It is sometimes necessary to group some of the terms of an expression. This can be accomplished by use of a set of parentheses.
When the grouping symbol is preceded by a plus sign. we keep the signs of the terms the same when it is preceded by a minus sign, we use the additive inverses (negatives) of the terms.
EXAMPLE Group the last three terms of the polynomial 3a - 5b + c - 2 with a grouping symbol in two ways, one preceded by a plus sign, the second preceded by a minus sign.
Solution
