Exponential and logarithmic function

5.1  EXPONENTIAL FUNCTIONS

  Recall from Chapter 1 the definition of a^r, where r is a rational number: if r = m/n, then for appropriate values of m and n,

  a^(m/n)=(root(n,a))^m

  For example

  16^(3/4)=(root(4,16))^3=2^3=8,

  27^-(1/3)=1/(27^(1/3))=1/(root(3,27))=1/3,

  and  64^-(1/2)=1/(64^(1/2))=1/(root(64))=1/8.

  In this section the definition of a^r is extended to include all real (not just rational) values of the exponent r. For example, the new symbol 2^(root(3) might be evaluated by approximating the exponent root(3) by the numbers 1.7,1.73,1.732. and so on. Since these decimals approach the value of root(3) more and more closely, it seems reasonable that 2^(root(3) should be approximated more and more closely by the numbers to 2^(1.7),2^(1.73),2^(1.732), and so on. (Recall, for example. that 2^(1.7)=2^(17/10)=root(10,2^17)) In fact. this is exactly how 2^(root(3) is defined (in a more advanced course).

  With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter. For example, if y=2^x, then each real value of x leads to exactly one value of
y, and therefore. y=2^x defines a function. Furthermore,

  if 3^x=3^4, then x=4,

  and for p>0,

  if p^2=3^2, then p=3.

  Also,  4^2<4^3 but (1/2)^2>(1/2)^3,

  so that when a > 1, increasing the exponent on a leads to a larger number, but if 0 < a < 1, increasing the exponent on a leads to a smaller number.

  These properties are generalized below. Proofs of the properties are not given here, as they require more advanced mathematics.

  ADDITIONAL PROPERTIES OF EXPONENTS

  (a) If a > 0 and a!=1, then a^x is a unique real number for all real numbers x.
  (b) In a>0 and a!=1, then a^b=a^c if and only if b=c.

  (c) If a > 1 and m < n, then a^m<a^n.

  (d) If 0 < a < 1 and m < n , then a^m>a^n.

  Properties (a) and (b) require a>0 so that a^x is always defined. For example, (-6)^x is not a real number if x = 1/2. This means that a^x will always he positive, since a is positive. In part (a), a!=1 because 1^x=1 for every real-number value of x, so that each value of x does not lead to a distinct real number. For Property (b) to hold, a must not equal 1 since, for example. 1^4=1^5, even though 4!=5.

EXPONENTIAL EQUATIONS The properties given above are useful in solving equations, as shown by the next examples.

Example 1

USING A PROPERTY OF EXPONENTS TO SOLVE AN EQUATION

  Solve (1/3)^x=81.

  First, write 1/3 as 3^-1, so that (1/3)^x=3^(-x). Since 81=3^4,

  (1/3)^x=81

  becomes

  By the second property above,

  -x=4,  or  x=-4.

  The solution set of the given equation is {-4}.

  In Section 5.4 we describe a more general method for solving exponential equations where the approach used in Example 1 is not possible. For instance, this method could not be used to solve an equation like 7^x=12, since it is not easy to express both sides as exponential expressions with the same base.

Example 2

USING A PROPERTY OF EXPONENTS TO SOLVE AN EQUATION

  Solve 81=b^(4/3).

  Being by writing b^(4/3) as (root(3,b))^4.

  81=b^(4/3)

  81=(root(3,b))^4

  +-3=root(3,b)  Take fourth roots on both sides.

  +-27=b  Cubs both sides.

  Check both solutions in the original equation. Since both solutions check, the solution set is {-27,27}. 

  GRAPHING EXPONENTIAL FUNCTIONS As mentioned above, the expression a^x satisfies all the properties of exponents from Chapter 1. We can now define a function f(x) = a^x whose domain is the set of all real numbers (and not just the rationals).

EXPONENTIAL FUNCTION  If a>0 and a!=1, then

  f(x) = a^x

  defines the exponential function with base a.

NOTE  If a=1, the function is the constant function f(x) = 1, and not an exponential function.

Example 3

EVALUATING AN EXPONENTIAL EXPRESSION

  If f(x)=2^x, find each of the following.

  (a) f(-1)

  Replace x with -1.

  f(-1)=2^-1=1/2

  (b) f(3)=2^3=8

  (c) f(5/2)=2^(5/2)=(2^5)^(1/2)=32^(1/2)=root(32)=4root(2)

  Figure 5.1 shows the graph of f(x)=2^x. The graph was found by obtaining a number of ordered pairs belonging to the function and then drawing a smooth curve through them. As we choose smaller and smaller negative values of x, the yy-values get closer and closer to 0, as shown in the table below.

x	0	-1	-2	-3	-4
y	1	1/2	1/4	1/8	1/16

  

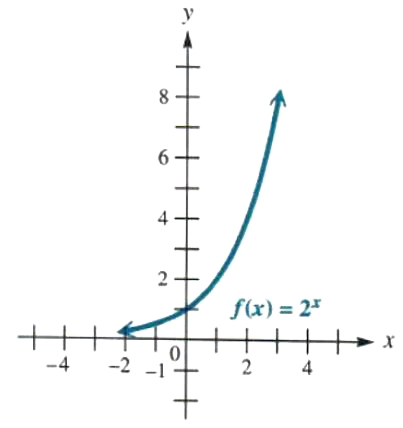
  FIGURE 5.1

  Because 2^x is always positive, the values of y will never become 0. The line y = 0. which the graph gets closer and closer to, is called a horizontal asymptote . Asymptotes will be discussed in more detail in Chapter 6. By Property (c), as x increases, so does y, making f(x) = 2^x an increasing function. As suggested by the graph in Figure 5.1, the domain of the function is (-∞,∞), and the range is (0,∞).

  

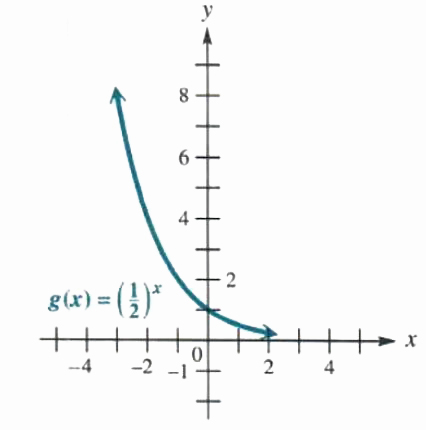
  Figure 5.2

  In Figure 5.2, the graph of g(x) = (1/2)^x was sketched in a similar way. The domain and range are the same as those of f(x) = 2^x. However, here, as the values of x increase. the values of y decrease, so g(x) = (1/2)^x is a decreasing function. The graph of g(x) = (1/2)^x is the reflection of the graph of f(x) = 2^x across the  y-axis, because g(x) = f(-x).

  As the graphs suggest, by the horizontal line test, f(x) = 2^x and g(x) = (1/2)^x are one-to-one functions.

  The graph of f(x) = 2^x is typical of graphs of f(x) = a^x. where a>1. For larger values of a. the graphs rise more steeply, but the general shape is similar to the graph in Figure 5.1. Exponential functions with 0 < a < 1 have graphs similar to that of g(x) = (1/2)^x. Based on our work above, the following generalizations can be made about the graphs of exponential functions defined by f(x) = a^x.

GRAPH OF f(x) = a^x

  1. The point (0, 1) is on the graph.

  2. If a > 1, f is an increasing function; if 0 < a < 1, f is a decreasing function.

  3. The x-axis is a horizontal asymptote.

  4. The domain is (-∞,∞) and the range is (0,∞).

  We can use the composition of functions lo produce more general exponential functions. If h(u)=ka^u, where k is a constant and u = g(x), and f(x) = h[g(x)], then

  f(x)=h[g(x)]=ka^(g(x))

  For example, if a=7,g(x)=3x-1, and k=4, then

  f(x)=4*7^(3x-1)

Example 4

GRAPHING A COMPOSITE EXPONENTIAL FUNCTION

  Graph f(x)=2^(-x+2) The graph will have the same shape as the graph of g(x)=2^(-x)=(1/2)^x. Because of the 2 added to -x, the graph will be translated 2 units to the right, compared with the graph of g(x)=2^(-x). This means that the point (2,1) is on the graph instead of (0,1). When x=0, y=2^2=4, so the point (0, 4) is on the graph. Plotting a few additional points, such as (-1, 8) and (1. 2), gives the graph in Figure 5.3. The graph of g(x)=2^(-x) is also shown for comparison. 

  

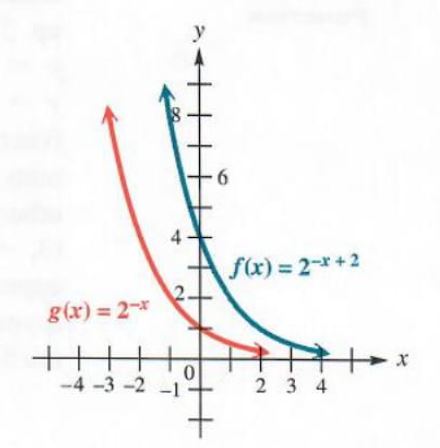
  Figure 5.3

IN SIMPLEST TERMS

  The exponential growth of deer in Massachusetts can be calculated using the equation t=50,000(1+0.06)^n, where 50,000 is the initial deer population and .06 is the rate of growth This the total population after n years have passed.

  Given the initial population and growth rate above, We could predict the total population after 4 years by using n = 4.

  T=50,000(1+0.06)^4

  ≈50,000(1.26)

  =63,000

  We can expect a total population of about 63,000, or an increase of about 13000 deer.

Example 5

GRAPHING A COMPOSITE EXPONENTIAL FUNCTION

  Graph f(x)=-2^x+3 

  The graph of y=-2^x is a reflection across the x-axis of the graph of y=2^x.The 3 indicates that the graph should be translated up 3 units, as compared to the graph of y=-2^x. Find some ordered pairs. Since y=-2^x would have y-intercept -1, this function has y-intercept 2, which is up 3 units from the y-intercept of y=-2^x. Some other ordered pairs are (1,1),(2,-1), and (3, -5). For negative values of x, the graph approaches the line y = 3 as a horizontal asymptote. The graph is shown in Figure 5.4. 

  

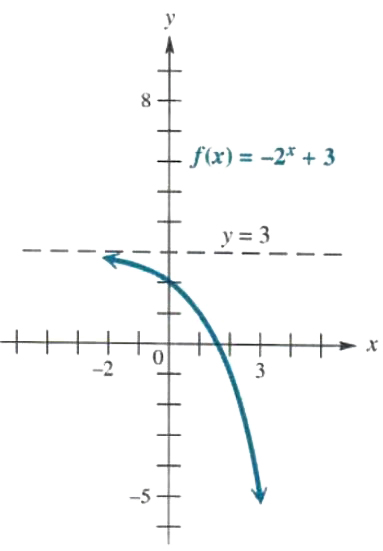
  Figure 2.4

Example 6

GRAPHING A COMPOSITE EXPONENTIAL FUNCTION

  Graph f(x)=2^(-x^2).

  Write f(x)=2^(-x^2) as f(x)=1/(2^x^2)to find ordered pairs that belong to the function. Some ordered pairs are shown in the chm below.

  

x	-2	-1	0	1	2
y	1/16	1/2	1	1/2	1/16

  As the chant suggests, 0<y<=1 for all values of x. Plotting these points and drawing a smooth curve through them gives the graph in Figure 5.5. This graph is symmetric with respect to the y-axis and has the x-axis as a horizontal asymptote. 

  

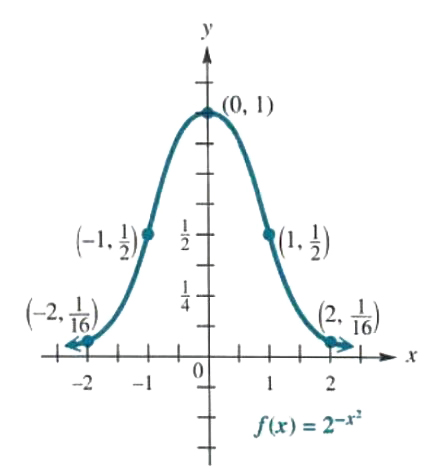
  Figure 5.5

  The important normal curve in probability theory has a graph very similar to me
one in Figure 5.5.

  COMPOUND INTEREST The formula for compound interest (interest paid on both principal and interest) is an important application of exponential functions. You may recall the formula for simple interest, {Iota}=Prt, where P is the amount left at interest, r is the rate of interest expressed as a decimal, and t is time in years that the principal earns interest. Suppose t=1 year. Then at the end of the year the amount has grown to

  P+Pr=P(1+r),

  the original principal plus the interest. If this amount is left at the same interest rate for another year, the total amount becomes

  [P(1+r)]+[P(1+r)]r

  =[P(1+r)](1+r)

  =P(1+r)^2

  After the third year, this will grow to

  [P(1+r)^2]+[P(1+r)^2]r

  =[P(1+r)^2](1+r)

  =P(1+r)^3.

  Continuing in this way produces the following formula for compound interest.

COMPOUND INTEREST

  If P dollars is deposited in an account paying an annual rate of interest r compounded (paid) m times per year, then after t years the account will contain A dollars, where

  A=P(1+r/m)^(tm).

  For example, let $1000 be deposited in an account paying 8% per year compounded quarterly, or four times per year. After 10 years the account will contain

  P(1+r/m)^(tm)

  =1000(1+(0.08)/4)^(10(4))

  =1000(1+0.02)^(40)

  =1000(1.02)^40

  dollars. The number (1.02)^40 can be found by using a calculator with a y^x key. To five decimal places, (1.02)^40=2.20804. The amount on deposit after 10 years is

  1000(1.02)^40=1000(2.20804)=2208.04,

  or $2208.04

  In the formula for compound interest. A is sometimes called the future value and P the present value.

Example 7

FINDING PRESENT VALUE

  An accountant wants to buy a new computer in three years that will cost $20,000.

  (a) How much should be deposited now, at 6% interest compounded annually, to give the required $20,000 in three years?

  Since the money deposited should amount to $20,000 in three years, $20,000 is the future value of the money. To find the present value P of $20,000 (the amount to deposit now), use the compound interest formula with A = 20,000, r=0.06,m=1,and t=3.

  A=P(1+r/m)^(tm)

  20,000=P(1+(0.06)/1)^(3(1))=P(1.06)^3

  (20,000)/((1.06)^3)=P

  P=16,792.39

  The accountant must deposit $16,792.39.

  (b) If only $15,000 is available to deposit now, what annual interest rate is required for it to increase to $20,000 in three years?

  Here P = 15,000, A = 20,000, m = 1, t= 3, and r is unknown. Substitute the known values into the compound interest formula and solve for r.

  A=P(1+r/m)^(tm)

  20,000=15,000(1+r/1)^3

  4/3=(1+r)^3  Divide both sides by 15,000

  (4/3)^(1/3)=1+r  Take the cubs root on both sides.

  (4/3)^(1/3)-1=r  Subtract 1 on both sides

  r≈  0.10  Use a calculator.

  An interest rate of 10% will produce enough interest to increase the $15,000 deposit to the $20,000 needed at the end of three years. 

  Perhaps the single most useful exponential function is the function defined by f(x) =e^x, where e is an irrational number that occurs often in practical applications. The number e comes up in a natural way when using the formula for Compound interest.

  Suppose that a lucky investment produces an annual interest of 100%, so that r=1.00, or r=1. Suppose also that only $11 can be deposited at this rate, and for only one year. Then P=1 and t=1. Substitute into the formula for compound interest:

  

m	(1+1/m)^m
1	2
2	2.25
5	2.48832
10	2.59374
25	2.66584
50	2.69159
100	2.70481
500	2.71557
1000	2.71692
10,000	2.71815
1000000	2.71828

P(1+r/m)^(tm)=1(1+1/m)^(1(m))=(1+1/m)^m

  As interest is compounded more and more often, the value of this expression will increase. If interest is compounded annually, making m = 1, the total amount on deposit is

  (1+1/m)^m=(1+1/1)^1=2^1=2,

  so an investment of $1 becomes $2 in one year.

  A calculator with a y^x key gives the results in the table at the left. These results have been rounded to five decimal places. The table suggests that, as m increases, the value of (1+1/m)^m gets closer and closer to some fixed number. It turns out that this is indeed the case. This fixed number is called e.

VALUE OF e  To nine decimal places,

  e≈ 2.718281828

NOTE  Values of e^x can be found with a calculator that has a key marked e^x or by using a combination of keys marked INV and ln x. See your instruction booklet for details or ask your instructor for assistance. 

   In Figure 5.6 the functions y=2^x, y=e^x, and y=3^x are graphed for comparison.

  

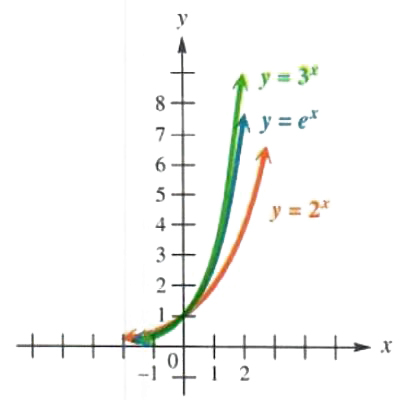
  Figure 5.6

  

EXPONENTIAL GROWTH| AND DECAY As mentioned above, the number e is important as the base of an exponential function because many practical applications require an exponential function with base e. For example, it can be shown that in situations involving growth or decay of a quantity, the amount or number present at time t often can be closely approximated by a function defined by

  A=A_0e^(kt),

  where A_0 is the amount or number present at time t = 0 and k is a constant.

  The next example illustrates exponential growth.

Example 8

SOLVING AN EXPONENTIAL GROWTH PROBLEM

  The U. S. Consumer Price Index (CPI, or cost of living index) has risen exponentially over the years. From 1960 to 1990, the CPI is approximated by

  A(t)=34e^(0.04t)

  where t is time in years, with t=0 corresponding to 1960. The index in 1960, at t=0, was

  A(0)=34e^((0.04)(0))

  =34e^0

  =34.  e^0=1

  To find the CPI for 1990, let t=1990-1960=30, and find A(30).

  A(30)=34e^((0.04)(30))

  =34e^(1.2)

  =113  e^(1.2)≈ 3.3201

  The index measures the avenge change in prices relative to the base year 1983 (1983 corresponds to 100) of a common group of goods and services. Our result of 113 means that prices increased an average of 113-34=79 percent over the 30-year period from 1960 to 1990. 

5.2  LOGARITHMIC FUNCTIONS

  The previous section dealt with exponential functions of the form y=a^x for all positive values of a, where a!=1. As mentioned there, the horizontal line test shows that exponential functions are one-to-one. and thus have inverse functions. In this section we discuss the inverses of exponential functions. The equation defining the inverse of a function is found by exchanging x and y in the equation that defines the function. Doing so with y=a^x gives

  a=a^y

  as the equation of the inverse function of the exponential function defined by y=a^x. This equation can be solved for y by using the following definition.

LOGARITHM

  For all real numbers y, and all positive numbers a and x, where a!=1:

  y=log_a(x) if and only x=a^y.

  The "log" in the definition above is an abbreviation for logarithm. Read log_a(x) as “the logarithm to the base a of x." Intuitively, the logarithm to the base a of x is the power to which a must be raised to yield x.

  In working with logarithms, it is helpful to remember the following.

MEANING OF log_a(x) 

  A logarithm is an exponent; log_a(x) is the exponent on the base a that yields the number x. 

  The “log” in y=log_a(x) is the notation for a particular function and there must be a replacement for x following it, as in log_a(3), log_a(2x-1), or log_a(x^2). Avoid writing meaningless notation such as y=log or y=log_a.

Example 1

CONVERTING BETWEEN EXPONENTIAL AND LOGARITHMIC STATEMENTS

  The chart below shows several pairs of equivalent statements. The same statement is written in both exponential and logarithmic forms. 

Exponential Form	Logarithmic Form
2^3=8	log_2(8)=3
(1/2)^-4=16	log_(1/2)16=-4
10^5=100,000	log_10(100,000)=5
3^(-4)=1/81	log_3(1/81)=-4
5^1=5	log_5(5)=1
(3/4)^0=1	log_(3/4)1=0

  LOGARITHMIC EQUATIONS The definition of logarithm can be used to solve logarithmic equations, as shown in the next example.

Example 2

SOLVING LOGARITHMIC EQUATIONS

  Solve each equation.

  (a) log_x(8/27)=3

  First, write the expression in exponential form.

  x^3=8/27

  x^3=(2/3)^3  8/27=(2/3)^3

  x=2/3  property (b) of exponents

  The solution set is {2/3}.

  (b) log_4(x)=5/2

  In exponential form, the given statement becomes

  4^(5/2)=x

  (4^(1/2))^5=x

  2^5=x

  32=x

  The solution set is {32}.

  LOGARITHMIC FUNCTIONS The logarithmic function with base a is defined as follows.

LOGARITHMIC FUNCTIONS

  If a>0,a!=1, and x>0, then

  f(x)=log_a(x)

  defines the logarithmic function with base a.

  Exponential and logarithmic functions are inverses of each other. Since the domain of an exponential function is the set of all real numbers. the range of a logarithmic function also will be the set of all real numbers. In the same way, both the range of an exponential function and the domain of a logarithmic function are
the set of all positive real numbers, so logarithms can be found for positive numbers only.

  The graph of y=2^x is shown in red in Figure 5.7. The graph of its inverse is found by reflecting the graph of y = 2^x about the line y = x. The graph of the inverse function. defined by y=log_2(x), shown in blue. has the y-axis as a vertical asymptote.

  

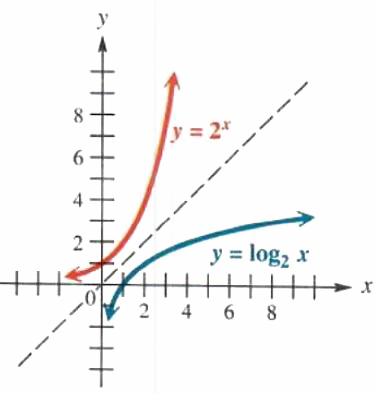
  Figure 5.7

  

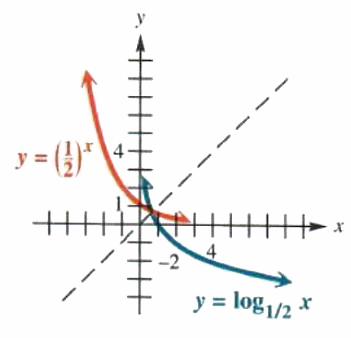
  Figure 5.8

  The graph of y=(1/2)^x is shown in red in Figure 5.8. The graph of its
inverse, defined by y=log_(1/2)x, in blue, is found by reflecting the graph of y = (1/2)^xabout the line y = x. As Figure 5.8 suggests, the graph of y=log_(1/2)x also has the y-axis for a vertical asymptote.

  The graphs of y = log_2x in Figure 5.7 and y=log_(1/2)x in Figure 5.8 suggest the following generalizations about the graphs of logarithmic functions of the form f(x) = log_a(x).

GRAPH OF f(x)=log_a(x)

  1. The point (1, 0) is on the graph.

  2. If a > 1, f is an increasing function; if 0 < a < 1, f is a decreasing function.

  3. The y-axis is a vertical asymptote.

  4. The domain is (0,∞) and the range is (-∞,∞).

  Compare these generalizations to those for exponential functions discussed in Section 5.1.

  More general logarithmic functions can be obtained by forming the composition of h(x) = log_a(x) with a function g(x) to get

  f(x)=h[g(x)]=log_a[g(x)]

  The next examples illustrate some composite functions of this type.

Example 3

GRAPHING A COMPOSITE LOGARITHMIC FUNCTION

  Graph f(x)=log_2(x-1).

  The graph of this function will be the same as that of f(x) = log_2(x), but shifted1 unit to the right because x-1 is given instead of x. This makes the domain (1,∞) instead of (0,∞). The line x = 1 is a vertical asymptote. The range is (-∞,∞). Sec Figure 5.9. 

  

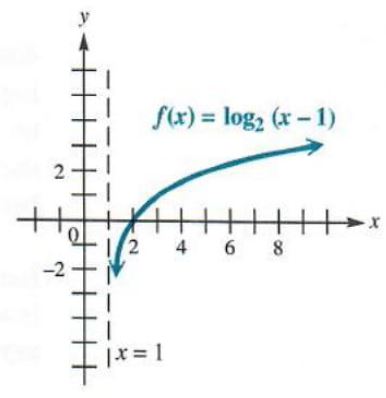
  Figure 5.9

Example 4

GRAPHING A TRANSLATED LOGARITHMIC FUNCTION

  Graph f(x)=(log_3x)-1.

  This function will have the same graph as that of g(x) = log_3x translated down 1 unit. A table of values is given below for both g(x) = log_3x and f(x)=(log_3x)-1.

x	1/3	1	3	9
g(x)	-1	0	1	2
f(x)	-2	-1	0	1

  The graph is shown in Figure 5.10.

  

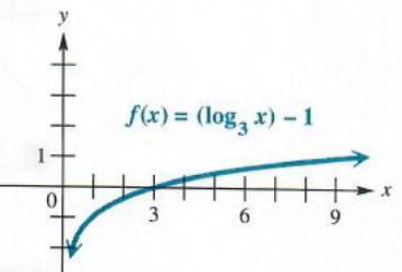
  Figure 5.10

Example 5

GRAPHING A COMPOSITE LOGARITHMIC FUNCTION

  Graph y=log_3|x|.

  Write y=log_3|x| in exponential form as 3^y=|x| to help identify some ordered pairs that satisfy the equation. (This is usually a good idea when graphing a logarithmic function.) Here. it is easier to choose y-values and find the corresponding x-values. Doing so gives the following ordered pairs.

x	-3	-1	-1/3	1/3	1	3
y	1	0	-1	-1	0	1

  Plotting these points and connecting them with a Smooth curve gives the graph in Figure 5.11. The y-axis is a vertical asymptote. Notice that, since y=log_3|-x|=log_3|x|, the graph is symmetric with respect to the y-axis. 

    

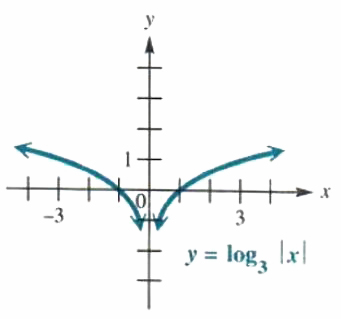
  Figure 5.11

CAUTION  If you write a logarithmic function in exponential form, choosing y-values to calculate x-values as we did in Example 5, be careful to get the ordered pairs in the correct order.

PROPERTIES OF LOGARITHMS  Logarithms originally were important as an aid for numerical calculations, but the availability of inexpensive calculators has made this application of logarithms obsolete‘ Yet the principles behind the use of logarithms for calculation are important; these principles are based on the properties listed below.

PROPERTIES OF LOGARITHMS

  For any positive real numbers x and y, real number r, and any positive real number a, a != 1:

  (a) log_a(xy)=log_a(x)+log_a(y)

  (b) log_a(x/y)=log_a(x)-log_a(y)

  (c) log_a(x^r)=rlog_a(x)

  (d) log_a(a)=1

  (e)log_a(1)=0

PROOF

  To prove Property (3), let

  m=log_a(x)  and  n=log_a(y).

  By the definition of logarithm,

  a^m=x  and  a^n=y.

  Multiplication gives

  a^m*a^n=xy.

  By a Property of exponents,

  a^(m+n)=xy.

  Now use The definition of logarithm to write

  log_a(xy)=m+n.

  Since m=log_a(x) and n=log_a(y).

  log_a(xy)=log_a(x)+log_a(y).

  Properties (b) and (c) are proven in a similar way. (See Exercises 68 and 69.) Properties (d) and (e) follow directly from the definition of logarithm since a^1=a and a^0=1.
The properties of logarithms are useful for rewriting expressions with logarithms in different forms, as shown in the next examples.

Example 6

USING THE PROPERTIES OF LOGARITHMS

  Assuming that all variables represent positive real numbers, use the properties of logarithms to rewrite each of the following expressions.

  (a) log_6(7*9)

  log_6(7*9)=log_6(7)+log_6(9)

  (b) log_9(15/7)

  log_9(15/7)=log_9(15)-log_9(7)

  (c) log_5root(8)

  log_5root(8)=log_5(8^(1/2))=1/2log_5(8)

  (d) log_a((mnq)/(p^2))=log_a(m)+log_a(n)+log_a(q)-2log_a(p)

  (e) log_(a)root(3,m^2)=2/3log_a(m)

  (f) log_(b)root(n,(x^3y^5)/(z^m))

  =(1/n)log_b((x^3y^5)/(z^m)

  =1/n(log_b(x^3)+log_b(y^5)-log_b(z^m)

  =1/n(3log_b(x)+5log_b(y)-mlog_b(z))

  =(3/n)log_b(x)+(5/n)log_b(y)-(m/n)log_b(z)

  Notice the use of parentheses in the second step. The factor 1/n applies to each term. 

Example 7

USING THE PROPERTIES OF LOGARITHMS

  Use the properties of logarithms to write each of the following as a single logarithm with a coefficient of 1. Assume that all variables represent positive real numbers.

  (a) log_3(x+2)+log_3(x)-log_3(2)

  Using Properties (a) and (b),

  log_3(x+2)+log_3(x)-log_3(2)=log_3((x+2)x)/(2)

  (b) 2log_a(m)-3log_a(n)=log_a(m^2)-log_a(n^3)=log_a(m^2/n^3)

  Here we used Property (c), then Property (b).

  (c) 1/2log_b(m)+3/2log_b(2n)-log_b(m^2n)

  =log_b(m^(1/2))+log_b(2n)^(3/2)-log_b(m^2n)  Property (c)

  =log_b((m^(1/2)(2n)^(3/2))/(m^2n))  Properties (a) and (b)

  =log_b((2^(3/2)n^(1/2))/(m^(3/2))  Rules for exponents

  =log_b((2^3n)/(m^3))^(1/2)  Rules for exponents

  =log_b(root((8n)/(m^3))  Definition of a^(1/n)

CAUTION

  There is no property of logarithms to rewrite a logarithm or’ a sum or difference. That is why, in Example 7(a), log_3 (x + 2) was not written as log_3x+log_3(2) Remember, log_3x+log_3(2)=log_3(x*2).

Example 8

USING THE PROPERTIES OF LOGARITHMS WITH NUMERICAL VALUES

  Assume that log_10(2)=0.3010. Find the base 10 logarithms of 4 and 5.
  By the properties of logarithms,

  log_10(4)=log_10(2^2)=2log_10(2)=2(0.3010)=0.6020

  log_10(5)=log_10(10/2)=log_10(10)-log_10(2)=1-0.3010=0.6990.

  We used Property (d) to replace log_10(10) with 1.

  Compositions of the exponential and logarithmic functions can be used to get two more useful properties. If f(x)=a^x and g(x)=log_a(x), then

  f[g(x)]=a^(log_a(x))

  and  g[f(x)]=log_a(a^x)

THEOREM ON INVERSES

  For a>0, a!=1:

  a^(log_a(x))=x  and  log_a(a^x)=x

  PROOF

  Exponential and logarithmic functions are inverses of each other, so f[g(x)]=x and g[f(x)]=x. Letting f(x)=a^x and g(x)=log_a(x) gives both results. 

  By the results of the last theorem,

  log_5(5^3)=3,  7^(log_7(10))=10,  and    log_r(r^(k+1))=k+1.

   The second statement in the theorem will be useful in Sections 5.4 and 5.5 when solving logarithmic or exponential equations.

5.3  EVALUATING LOGARITHMS; CHANGE OF BASE

  COMMON LOGARITHMS Base 10 logarithms are called common logarithms. The common logarithm of the number x, or log_10(x). is often abbreviated as just log x, and we will use that convention from now on. A calculator with a log key can be used to find base 10 logarithms of any positive number.

Example 1.

EVALUATING COMMON LOGARITHMS

  Use a calculator to evaluate the following logarithms`.

  (a) log 142

  Enter 142 and press the log key. This may be a second function key on some calculators. With other calculators, these steps may be reversed. Consult your owner’s manual if you have any problem using this key. The result should be 2.152 to the nearest thousandth.

  (b) log 0.005832

  A calculator gives

  log0.005832≈-2.234.

NOTE  Logarithms of numbers less than 1 are always negative, as suggested by the graphs in Section 5.2.

  In chemistry, the pH of a solution is defined as

  pH=-log[H_3O^+0],

  where [H_3O^+0] is the hydronium ion concentration in moles per liter. The pH value is a measure of the acidity or alkalinity of solutions. Pure water has a pH of 7.0, substances with pH values greater than 7.0 are alkaline, and substances with pH values less than 7.0 are acidic.

Example 2.

FINDINGpH

  (a) Find the pH of a solution with [H_3O^+0]=2.5x10^-4

  pH=-log[H_3O^+0]

  pH=-log(2.5x10^-4)  Substitute.

  =-(log(2.5)+log10^-4)  Property (B) of logarithms

  =-(0.3979-4)

  =-0.3979+4

  =3.6

  It is customary to round pl-I values to the nearest tenth.

  (b) Find the hydronium ion concentration of a solution with pH = 7.1.

  pH=-log[H_3O^+0]

  7.1=-log[H_3O^+0]  Substitute.

  -7.1=log[H_3O^+0]  Multiply by -1.

  [H_3O^+0]=10^(-7.1)  Write in exponential form.

  Evaluate 10^(-7.1) with a calculator to get

  [H_3O^+0]≈  7.9x10^-8.

Example 3.

SOLVING AN APPLICATION OF BASE 10 LOGARITHMS

  The loudness of sounds is measured in a uni! called a decibel. To measure with this unit, we first assign an intensity of {Iota}_0 to a very faint sound, called the threshold sound. If a particular sound has intensity {Iota}, then the decibel rating of this louder sound is

  d=10log{Iota}/{Iota}_0.

  Find the decibel rating of a sound with intensity 10,000{Iota}_0

  d=10log(10,000{Iota}_0)/({Iota}_0)

  =10log10000

  =10(4)  log10000=4

  =40

  The sound has a decibel rating of 40.

  NATURAL LOGARITHMS In In most practical applications of logarithms, the number e≈2.718281828 is used as base. The number e is irrational, like PI. Logarithms to base e are called natural logarithms, since they occur in the life sciences and economics in natural situations that involve growth and decay. The base e logarithm of x is written ln x (read “el-en  x"). A graph of the natural logarithm function defined by f(x) = ln x is given in Figure 5.12. Natural logarithms can be found with a calculator that has an In key.

  

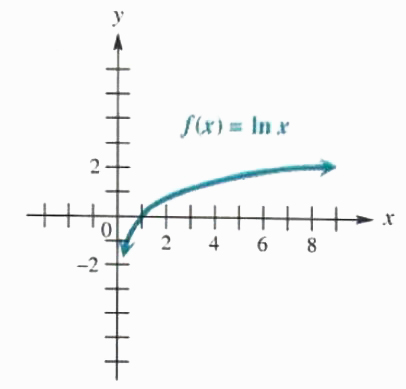
  Figure 5.12

Example 4

EVALUATING NATURAL LOGARITHMS

  Use a calculator to find the following logarithms.

  (a) In 85

  With a calculator, enter 85, press the In key, and read the result, 4.4427. The steps may be reversed with some calculators. If your calculator has an e^x key, but not a key labeled ln x, natural logarithms can be found by entering the number, pressing the {Iota}NV key and then the e^x key. This works because y=e^x is the inverse function of y=lnx (or y = log_e(x).

  (b) ln 127.8=4.850

  (c) ln0.049=-3.02

  As with common logarithms, natural logarithms of numbers between 0 and 1 are negative. 

Example 5

APPLYING NATURAL LOGARITHMS

  Geologists sometimes measure the age of rocks by using “atomic clocks." By measuring the amounts of potassium 40 and argon 40 in a rock, the age t of the specimen in years is found with the formula

  t=(1.26x10^9)(ln[1+8.33(A/K)])/(ln2)

  A and K are respectively the numbers of atoms of argon 40 and potassium 40 in the specimen.

  (a) How old is a rock in which A = 0 and K > 0?

  If A = 0, A/K = 0 and the equation becomes

  t=(1.26x10^9)(ln1)/(ln2)=(1.26x10^9)(0)=0

  The ruck is 0 years old or new.

  (b) The ratio A/K for a sample of granite from New Hampshire is 0.212. How old is the sample?

  Since A/K is 0.212, we have

  t=(1.26x10^9)(ln[1+8.33(0.212)])/(ln2)=1.85x10^9

  The granite is about 1.85 billion years old.

  LOGARITHMS TO OTHER BASES A calculator can be used to find the values of either natural logarithms (base e) or common logarithms (base 10). However, sometimes it is convenient to use logarithms to other bases. The following theorem can be used to convert logarithms from one base lo another.

CHANGE OF BASE THEOREM

  For any positive real numbers x, a, and b. where a!=1 and b !=1:

  log_a(x)=(log_b(x))/(log_b(a)

  This theorem is proved by using the definition of logarithm to write y = log_a(x) in exponential form.

PROOF

  Let  y=log_a(x)

  a^y=x  Change to exponential form

  log_b(a^y)=log_b(x)  Take logarithms on both sides

  ylog_b(a)=log_b(x)  Property (c) of logarithms

  y=(log_b(x))/(log_b(a))  Divide both sides by log_b(a). 

  log_a(x)=(log_b(x))/(log_b(a  Substitute log, x for y. 

  Any positive number other than 1 can be used for base b in the change of base rule, but usually the only practical bases are e and 10, since calculators give logarithms only for these two bases. 

NOTE  Some calculators have only a log key or an ln key. In that case, the change of base rule can be used to find logarithms to the missing base.

  The next example shows how the change of base rule is used to find logarithms to bases other than 10 or e with a calculator.

Example 6

USING THE CHANGE OF BASE RULE

  Use natural logarithms to find each of the following. Round to the nearest hundredth.

  (a) log_5(17)

  Use natural logarithms and the change of base theorem.

  log_5(17)=(log_e17)/(loge5)

  =(ln17)/(ln5)

  Now use a calculator to evaluate this quotient.

  log_5(17)≈(2.8332)/(1.69094)

  ≈1.76

  To check, use a calculator with a y‘ key, along with the definition of logarithm, to verify that 5^(1.76) ≈ 17.

  (b) log_2*1

  log_2*1=(ln*1)/(ln*2) ≈ (-2.3026)/(0.6931)=-3.32

NOTE

  In Example 6, logarithms that were evaluated in the intermediate steps, such as ln 17 and ln 5, were shown to four decimal places. However, the final answers were obtained without rounding off these intermediate values, using all the digits obtained with the calculator. In general, it is best to wait until the final step to round off the answer; otherwise, a build-up of round-off error may cause the final answer to have an incorrect final decimal place digit.

Example 7

SOLVING AN APPLICATION WITH BASE 2 LOGARITHMS

  One measure of the diversity of the species in an ecological community is given by the formula

  H=-[P_1log_2O_1+P_2log_2P_2+...+P_(n)log_2P_n],

  where P_1,P_2,...,P_n are the proportions of a sample belonging to each of n species found in the sample. For example, in a community with two species, where there are 90 of one species and 10 of the other, P_1 = 90/100 = 0.9 and P_2 = 10/100 = 0.1. Thus,

  H=-[0.9log_2(0.9)+0.1log_2(0.1)].

  Example 6(b), log_2(0.1) was found to be -3.32. Now find log_2(0.9)

  Therefore,

  H ≈ -[(0.9)(0.152)+(0.1)(-3.32)]≈ 0.469

   If the number in each species is the same, the measure of diversity is 1. representing “perfect” diversity. In a community with little diversity, H is close to 0. In this example, since H=0.5. there is neither great nor little diversity. 

5.4  EXPONENTIAL AND LOGARITHMIC EQUATIONS

  As mentioned at the beginning of this chapter, exponential and logarithmic functions are important in many useful applications of mathematics. Using these functions in applications often requires solving exponential and logarithmic equations. Some simple equations were solved in the first two sections of this chapter. More general methods for solving these equations depend on the properties below. These properties follow from the fact that exponential and logarithmic functions are one-to-one. Property 1 was given and used to solve exponential equations in Section 5.1.

PROPERTIES OF LOGARITHMIC AND EXPONENTIAL FUNCTIONS

  For b>0 and b!=1:

  1. b^x=b^y if and only if x=y.

  2. x>0 and y>0,

  log_b(x)=log_b(y) if and only if x=y.

  EXPONENTIAL EQUATIONS The first examples illustrate a general method, using Property 2, for solving exponential equations.

Example 1

SOLVING AN EXPONENTIAL EQUATION

  Solve the equation 7^x=12.

  In Section 5.1, we saw that Property 1 cannot be used to solve this equation, so we apply Property 2. While any appropriate base b can be used to apply Properly 2. the best practical base to use is base 10 or base e. Taking base e (natural) logarithms of both sides gives

  7^x=12

  ln7^x=ln12

  xln7=ln12  Property (c) of logarithms

  x=(ln12)/(ln7)  Divide by ln 7.

  A decimal approximation for x can be found using a calculator:

  x=(ln12)/(ln7) ≈ (2.4849)/(1.9459)≈ 1.277. 

  A calculator with a y^x key can be used to check this answer. Evaluate 7^(1.277); the result should be approximately 12. This step verifies that, to the nearest thousandth, the solution set is {1.277}. 

CAUTION

Be careful when evaluating a quotient like (ln12)/(ln7) in Example 1. Do not confuse
this quotient with ln(12/7) which can be written as ln 12 - ln 7. You cannot change the quotient of two logarithm to a difference of logarithms.

  (ln12)/(ln7)!=ln(12/7)

Example 2

SOLVING AN EXPONENTIAL EQUATION

  Solve e^(-2lnx)=1/16

  Use a property of logarithms to rewrite the exponent on the left side of the equation. 

  e^(-2lnx)=1/16

  e^(lnx^-2)=1/16  Property (0) of logarithms

  x^-2=1/16  Theorem on inverses: e^(lnk)=k

  x^-2=4^-2  1/16=1/4^2=4^-2

  x=4  Property 1 given above

  Check this answer by substituting in the original equation to see that the solution set is (4). 

  LOGARITHMIC EQUATIONS The next examples show some ways to solve logarithmic equations. The properties of logarithms given in Section 5.2 are useful here, as is Property 2.

Example 3

SOLVING A LOGARITHMIC EQUATION

  Solve log_a(x+6)-log_a(x+2)=log_a(x).

  Using a property of logarithms, rewrite the equation as

  log_a(x+6)/(x+2)=log_a(x)  Property (b) of logarithms

  Now the equation is in the proper form to use Property 2.

  (x+6)/(x+2)=x  Property 2

  (x+6)=x(x+2)  Multiby by x+2.

  x+6=x^2+2x  Distributive property

  x^2+x-6=0  Get 0 on one side.

  (x+3)(x-2)=0  Use the zero-factor property.

  x=-3  or  x=2.

  The negative solution (x = -3) cannot be used since it is not in the domain of log_a(x) in the original equation. For this reason, the only valid solution is the positive number 2, giving the solution set {2}. 

CAUTION

  Recall that the domain of y=log_b(x) is (0,∞). For this reason, it is always necessary to check that the solution of a logarithmic equation results in the logarithms of positive numbers in the original equation.

IN SIMPLEST TERMS

  When physicians prescribe medication they must consider how the drug's effectiveness decreases over time. If, each hour, a drug is only 90% as effective
as the previous hour, at some point the patient will not be receiving enough medication and must receive another dose. This situation can be modeled with a geometric sequence (see Section 9.2). If the initial dose was 200 mg and the drug was administered 3 hours ago, the expression 200(0.90)^2 represents the
amount of effective medication still available. Thus, 200(0.90)^2=162 mg are still in the system. To determine how long it would take for the medication to reach the dangerously low level of 50 mg, we consider the equation 200(0.90)^x=50, which is solved using logarithms.

  200(0.90)^x=50

  (0.90)^x=0.25

  log(0.90)^x=log(0.25)

  xlog(0.90)=log(0.25)

  x=(log(0.25))/(log(0.90))≈ 13.16

  Since x represents n - 1, the drug will reach a level of 50 mg in about 14 hours. 

Example 4

SOLVING LOGARITHMIC EQUATION

  Solve log(3x+2)+log(x-1)=1

  Since log x is an abbreviation for log_10(x), and 1=log_10(10), the properties of logarithms give

  log(3x+2)(x-1)=log10

  (3x+2)(x-1)=10  Property (a) of logarithms

  3x^2-x-2=10  Property 2

  3x^2-x-12=0

  Now use the quadratic formula to get

  x=(1+-root(1+144))/(6)

  If x=((1-root(145))/(6) , then x-1<0; therefore. log(x - l) is not defined and this proposed solution must be discarded, giving the solution set

  {(1+root(145))/(6)}.

  The definition of logarithm could have been used in Example 4 by first writing

  log(3x+2)+log(x-1)=1

  log_10(3x+2)(x-1)=1  Property (a)

  (3x+2)(x-1)=10^1  Definition of logarithm

  then continuing as shown above.

Example 5

SOLVING A LOGARITHMIC EQUATION

  Solve lne^(lnx)-ln(x-3)=ln2

  On the left,ln e^(lnx)can be written as lnx using the theorem on inverses at the end of Section 5.2. The equation becomes

  lnx-ln(x-3)=ln2

  ln(x/(x-3))=ln2  Property (b)

  x/(x-3)=2  Property 2

  x=2x-6  Multiply by x-3.

  6=x.

  Verify that the solution set is {6}.

  A summary of the methods used for solving equations in this section follows.

SOLVING EXPONENTIAL AND LOGARITHMIC EQUATIONS

  An exponential or logarithmic equation may be solved by changing the equation into one of the following forms, where a and b are real numbers, a > 0, and a!=1.

  1. a^(f(x))=b

  Solve by taking logarithms of each side. (Natural logarithms are often a good choice.)

  2. log_(a)f(x)=log_(a)g(x)

  From the given equation, f(x) = g(x), which is solved algebraically.

  3. log_(a)f(x) = b

  Solve by using the definition of logarithm to write the expression in exponential form as f(x) = a^b.

  The next examples show applications of exponential and logarithmic equations.

Example 6

SOLVING A COMPOSITE EXPONENTIAL EQUATION

  The strength of a habit is a function of the number of times the habit is repeated. If N is the number of repetitions and H is the strength of the habit, then, according to psychologist C. L. Hull,

  (H)/(1000)=1-e^(-kN)  Divide by 1000.

  (H)/(1000)-1=-e^(-kN)  Subtract 1.

  e^(-kN)=1-(H)/(1000)  Multiply by -1.

  Now solve for k. As shown earlier, we take logarithms on each side of the equation and use the fact that ln e^x = x.

  lne^(-kN)=ln(1-(H)/(1000))

  -kN=ln(1-(H)/(1000))  lne^x=x

  k=-1/(N)ln(1-(H)/(1000))  Multiply by -1/(N).

  With the last equation, if one pair of values for H and N is known, k can be found, and the equation can then be used to find either H or N, for given values of the other variable. 

Example 7

SOLVING COMPOSITE LOGARITHMIC EQUATION

  In the exercises for Section 5.3, we saw that the number of species in a sample is given by S, where

  S=aln(1+n/a),

  n is the number of individuals in the sample, and a is a constant. Solve this equation for n.

  We begin by solving for (1+n/a) Then we can change to exponential form and solve the resulting equation for n.

  S/a=ln(1+n/a)  Divide by a.

  e^(S/a)-1=n/a Write in exponential form

  e^(S/a)-1=n/a  Subtract 1.

n=a(e^(S/a)-1))  Multiply by a.

  Using this equation and given values of S and a, the number of species in a sample can be found. 

5.5  EXPONENTIAL GROWTH AND DECAY

  In many cases, quantities grow or decay according to a function defined by

  A(t)=A_0e^(kt).

  As mentioned in Section 5.1, when k is positive, the result is a growth function; when k is negative, it is a decay function. This section gives several examples of applications of this function.

  CONTINUOUS COMPOUNDING The compound interest formula

  A=P(1+r/m)^(tm)

  was discussed in Section 5.1. The table presented there shows that increasing the frequency of compounding makes smaller and smaller differences in the amount of interest earned. In fact, it can be shown that even if interest is compounded at intervals of time as small as one chooses (such as each hour, each minute. or each second), the total amount of interest earned will be only slightly more than for daily compounding. This is true even for a process called continuous compounding. As suggested in Section 5.1, the value of the expression (1+1/m)^m approaches e as m gets larger. Because of this, the formula for continuous compounding involves the number e.

  CONTINUOUS COMPOUNDING If P dollars is deposited at a rate of interest r compounded continuously for t years, the final amount on deposit is

  A=Pe^(rt)

  dollars.

Example 1

SOLVING A CONTINUOUS COMPOUNDING PROBLEM

  Suppose $5000 is deposited in an account paying 8% compounded continuously for five years. Find the total amount on deposit at the end of five years.

  Let P=5000, t=5, and r=0.08/ Then

  A=5000e^(0.08(5))=5000e^4

  Using a calculator. we find that e^(0.4)≈ 1.49182, and

  A=5000e^(0.4)=7459.12,

  or $7459.12. As a comparison, the compound interest formula with daily compounding gives 

  A=P(1+r/m)^(tm)

  =5000(1+(0.08)/365)^(5(365))=7458.80,

  about 32¢ less.

Example 2

SOLVING CONTINUOUS COMPOUNDING PROBLEM

  How long will it take for the money in an account that is compounded continuously at 8% interest to double?

  Use the formula for continuous compounding, A=Pe^(rt), to find the time t that makes A=2P Substitute 2P for A and 0.08 for r, then solve for t.

  A=Pe^(rt)

  2P=Pe^(0.08t)  Substitute.

  2=e^(0.08t)  Divide by P.

  Taking natural logarithms on both sides gives

  ln2=lne^(0.08t).

  Use the property lne^x=x to get lne^(0.08t)=0.08t.

  ln2=0.08t

  (ln2)/(0.08)=t  Substitute.

  8.664=t  Divide by 0.08.

  It will take about 8 2/3 years for the amount to double.

  GROWTH AND DECAY The next examples illustrate applications of exponential growth and decay.

Example 3

SOLVING AN EXPONENTIAL DECAY PROBLEM

  Nuclear energy derived from radioactive isotopes can be used to supply power to space vehicles. The output of the radioactive power supply for a certain satellite is given by the function

  y=40e^(-0.004t),

  where y is in watts and t is the time in days.

  (a) How much power will be available at the end of 180 days?

  Let t=180 in the formula.

  y=40e^(-0.004(180))

  y≈ 19.5  Use a calculator.

  (b) How long will it take for the amount of power to be half of its original strength?

  The original amount of power is 40 watts. (Why?) Since half of 40 is 20, replace y with 20 in the formula, and solve for t. 

  20=40e^(-0.004t)

  0.5=e^(-0.004t)  Divide by 40

  ln0.5=lne^(-0.004t)

  ln0.5=-0.004t  lne^x=x

  t=(ln(1/2))/(-0.004)

  t≈ 173   Use a calculator.

  After about 173 days, the amount of available power will be half of its original amount. 

  In Examples 2 and 3(b), we found the amount of time that it would take for an amount to double and to become half of its original amount. These are examples of doubling time and half-life. The doubling time of a quantity that grows exponentially is the amount of time that it takes for any initial amount to grow to twice its value. Similarly, the half-life of a quantity that decays exponentially is the amount of time that it takes for any initial amount to decay to half its value.

Example 4

SOLVING AN EXPONENTIAL

  Carbon 14 is a radioactive form of carbon that is found in all living plants and animals. After a plant or animal dies, the radiocarbon disintegrates. Scientists determine the age of the remains by comparing the amount of carbon 14 present with the amount found in living plants and animals. The amount of carbon 14 present after t years is given by the exponential equation

  A(t)=A_0e^(kt)

  With k≈ -(ln2)(1/5700).

  (a) Find the half-life.

  Let A(t)=(1/2)A_0 and k=-(ln2)(1/5700).

  1/2A_0=A_0e^(-(ln2)(1/57000t)

  1/2=e^(-(ln2)(1/5700)t)  Divide by A_0.

  ln(1/2)=lne^(-(ln2)(1/5700)t)  Take logarithms on both sides.

  ln(1/2)=-(ln2)/(5700)t  lne^x=x

  -5700/(ln2)ln(1/2)=t  Multiply by -5700/(ln2)

  -5700/(ln2)(ln1-ln2)=t  Property (b)

  -5700/(ln2)(-ln2)=t  ln1=0

  5700=t

  The half-life is 5700 years.

  (b) Charcoal from an ancient fire pit on Java contained 1/4 the carbon 14 of a living sample of the same size. Estimate the age of the charcoal.

  Let A(t)=1/4A_0 and k=-(ln2)(1/5700).

  1/4A_0=A_0e^(-(ln2)(1/5700)t)

  1/4=e^(-(ln2)(1/5700)t)

  ln(1/4)=lne^(-(ln2)(1/5700)t)

  ln(1/4)=(ln2)/(5700)t

  -5700/(ln2)ln(1/4)=t

  t=11400

  The charcoal is about 11400 years old.