PERCENTAGES

Overview:

This section will explain how to apply algebra to percentage problems.

In algebra problems, percentages are usually written as decimals.

Example 1. Ethan got 80% of the questions correct on a test, and there were 55 questions. How many did he get right?

The number of questions correct is indicated by:

Ethan got 44 questions correct.

Explanation: % means "per one hundred". So 80% means 80/100 = 0.80.

Example 2. A math teacher, Dr. Pi, computes a student’s grade for the course as follows:

a. Compute Darrel's grade for the course if he has a 91 on the homework, 84 for his test average, and a 98 on the final exam.

Wrote percents as decimals.
G = 18.2 + 42 + 29.4
Multiplied
G = 89.6
Added

Darrel’s grade for the course is an 89.6, or a B+.

b. Suppose Selena has an 89 homework average and a 97 test average. What does Selena have to get on the final exam to get a 90 for the course?

The difference between Part a and Part b is that in Part b we don’t know Selena’s grade on the final exam.

So instead of multiplying 30% times a number, multiply 30% times E. E is the variable that represents what Selena has to get on the final exam to get a 90 for the course.

Set up the equation.
90 = 66.3 + 0.30E
Simplified
23.7 = 0.30E
Subtracted 66.3 from both sides.
79 = E
Divided both sides by 0.30

Because Selena studied all semester, she only has to get a 79 on the final to get a 90 for the course.

Example 3. Sink Hardware store is having a 15% off sale. The sale price of a toilet is $97; find the retail price of the toilet.

a. Complete the table to find an equation relating the sale price to the retail price (the price before the sale).

Vocabulary: Retail price is the original price to the consumer or the price before the sale.
Discount is how much the consumer saves, usually a percentage of the retail price.
Sale Price is the retail price minus the discount.

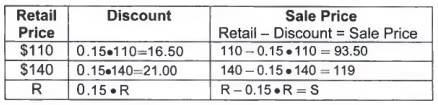
b. Simplify the equation.

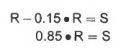
Explanation: The coefficient of R is one, so the arithmetic for combining like terms is 1 - 0.15 = .85. In other words, the sale price is 85% of the retail price.

c. Solve the equation when the sale price is $97.

The retail price for the toilet was $114.12. (Note: the answer was rounded to the nearest cent.)

The following diagram is meant as a visualization of problem 3.

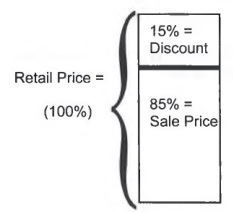
The large rectangle represents the retail price. The retail price has two components, the sale price and the discount. So
Retail Price = Sale Price + Discount
If Discount is subtracted from both sides of the equation, a formula for Sale Price is found.
Sale Price = Retail Price - Discount

Summary:

Percentages play an integral role in our everyday lives, including computing discounts, calculating mortgages, savings, investments, and estimating final grades.
When working with percentages, remember to write them as decimals, to create tables to derive equations, and to follow the proper procedures to solve equations.

Study Tip: Remember to use descriptive letters to describe the variables.

CHAPTER 1 REVIEW

This unit introduces algebra by examining similar models. You should be able to read a problem and create a table to find an equation that relates two variables. If you are given information about one of the variables, you should be able to use algebra to find the other variable.

Signed Numbers:

Informal Rules:

Adding or subtracting like signs: Add the two numbers and use the common sign.

Adding or subtracting unlike signs: Subtract the two numbers and use the sign of the larger, (more precisely, the sign of the number whose absolute value is largest.)

Multiplying or dividing like signs: The product or quotient of two numbers with like signs is always positive.

Multiplying or dividing unlike signs: The product or quotient of two numbers with unlike signs is always negative.

Order of operations: Please Excuse My Dear Aunt Sally
1. Inside Parentheses, ().
2. Exponents.
3. Multiplication and Division (left to right)
4. Addition and Subtraction (left to right)

Study Tip: All of these informal rules should be written on note cards.

Introduction to Variables:

Generate a table to find an equation that relates two variables.

Example 6. A car company charges $14.95 plus 35 cents per mile.

Simplifying Algebraic Equations:

Distributive property:

Combine like terms:

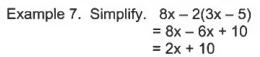
Solving Equations:

1. Simplify both sides of the equation.
2. Write the equation as a variable term equal to a constant.
3. Divide both sides by the coefficient or multiply by the reciprocal.
4. Three possible outcomes to solving an equation.
a. One solution ( a conditional equation )
b. No solution ( a contradiction )
c. Every number is a solution (an identity )

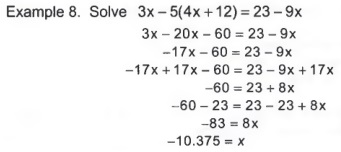
Applications of Linear Equations:

This section summarizes the major skills taught in this chapter.

Example 9. A cell phone company charges $12.50 plus 15 cents per minute after the first six minutes.

a. Create a table to find the equation that relates cost and minutes.

b. Simplify the equation.

c. If the call costs $23.50, how long were you on the phone?

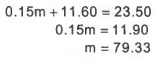
If the call costs $23.50, then you were on the phone for approximately 79 minutes.

Literal Equations:

A literal equation involves solving an equation for one of two variables.

Percentages:

Write percentages as decimals.

Example 11. An English teacher computes his grades as follows:

Sue has an 87 on the short essays and a 72 on the research paper. If she wants an 80 for the course, what grade does Sue have to get on the final?

Sue has to get a 78.36 in the final exam to get an 80 for the course.

Study Tips:

1. Make sure you have done all of the homework exercises.
2. Practice the review test on the following pages by placing yourself under realistic exam conditions.
3. Find a quiet place and use a timer to simulate the test period.
4. Write your answers in your homework notebook. Make copies of the exam so you may then re-take it for extra practice.
5. Check your answers.
6. There is an additional exam available on the Beginning Algebra web page.
7. DO NOT wait until the night before the exam to study.