Rules for Finding Derivatives
Finding the derivative of
![]()
involves computing the following limit:
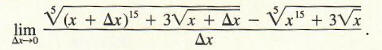
To put it mildly, this calculation would be unpleasant. We would like to find ways to compute derivatives without explicitly using the definition of the derivative as the limit of a difference quotient. A useful preliminary result is the following:
Derivative of a Constant
lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x . That is, the derivative of a constant function is the zero function.
It is easy to see this geometrically. Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal line. Since a horizontal line has slope 0, and the line is its own tangent, it follows that the slope of the tangent line is zero everywhere.
We next give a rule for differentiating f(x) = xn where n is any real number. Some of the following results have already been verified in the previous section, and the
others can be verified by using the definition of the derivative.
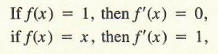
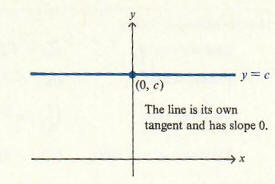
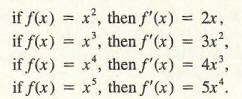
This pattern suggests the following general formula for powers of n where n is a positive integer.
Power Rule
![]()
In fact, the power rule is valid for any real number n and thus can be used to differentiate a variety of non-polynomial functions. The following example illustrates some applications of the power rule.
Example 1
Differentiate each of the following functions:
![]()
(a) Since f(x) = 5, f is a constant function; hence f '(x) = 0.
(b) With n = 15 in the power rule, f '(x) = 15x14
(c) Note that f(x) = x1/2 . Hence, with n = 1/2 in the power rule,
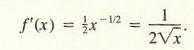
(d) Since f(x) = x-1, it follows from the power rule that f '(x) = -x-2 = -1/x2
The rule for differentiating constant functions and the power rule are explicit differentiation rules. The following rules tell us how to find derivatives of combinations of functions in terms of the derivatives of their constituent parts. In each case, we assume that f '(x) and g'(x) exist and A and B are constants.
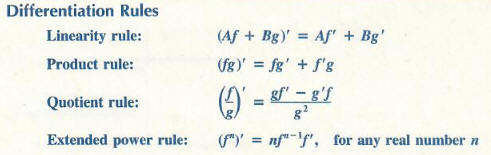
The four rules listed above, together with the rule on differentiating constant functions and the power rule, provide us with techniques for differentiating any function that is expressible as a power or root of a quotient of polynomial functions. The next series of examples illustrates this. The linearity rule and the product rule will be justified at the end of the section; a proof of the extended power rule appears in the section on the chain rule.
Example 2 Let
![]()
Find f '(x).
Solution Using the linearity rule, we see that
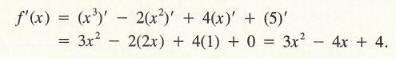
Example 3 Let
![]()
Again using linearity,
![]()
f'(x) = a(x3)' + b(x2)' + c(x)' + (d)' = 3ax^2 + 2bx + c
Example 3 can be generalized as follows:
A polynomial of degree n has a derivative everywhere, and the derivative is a polynomial of degree (n - 1).
Example 4 Let
![]()
Find f '(x).
First we use the product rule, since f(x) is given as the product of x2 and x2 - x + 1:
