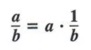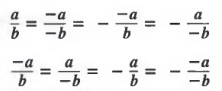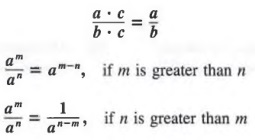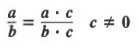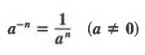PROPERTIES OF FRACTIONS

FORMS OF FRACTIONS: GRAPHICAL REPRESENTATIONS

As noted in Section 1.2, we often indicate the quotient of two numbers a ÷ b, b ≠ 0, by the fraction . We call a the numerator (or dividend) and b the denominator (or divisor).

Example 1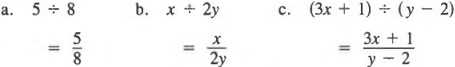

In Section 1.2 we defined a quotient to be a number q such that b · q = a

For example,

We can also view a quotient in terms of a product. For example,

In general,

Example 2

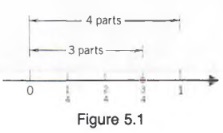
We can use this property to help us graph arithmetic fractions on a number line. For example, to graph the fraction , which is equivalent to , we divide a unit on the number line into four equal parts and then mark a point at the third quarter, as shown in Figure 5.1. In general, we can locate the graph of any fraction by dividing a unit on the number line into a number of equal parts corresponding to the denominator of the fraction, and then counting off the number of parts corresponding to the numerator.

Example 3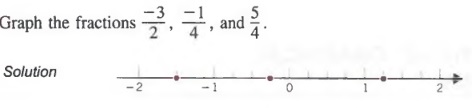

Fractions can involve algebraic expressions. In such cases, since division by 0 is undefined, we must restrict variables so that a divisor is never 0. In our work, we will assume that no denominator is 0 unless otherwise specified. For example,

SIGNS OF FRACTIONS

There are three signs associated with a fraction: the sign of the numerator, the sign of the denominator, and the sign of the fraction itself.

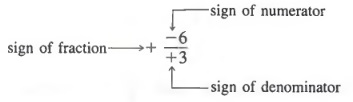
Fractions that have different signs may have the same value. For example,

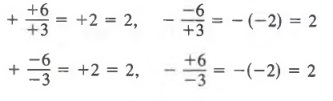
Each fraction above names the number 2.

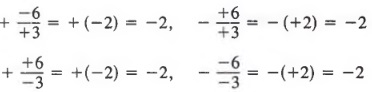
Each fraction above names the number -2.

The above examples suggest the following rule.

Any two of the three signs of a fraction may be changed without changing the value of the fraction.

For example,

In this book, the two forms and , which have positive signs on the denominator and on the fraction itself, will be considered standard forms for fractions. Sometimes answers are left in the form instead of the standard form .

Example 4 Write each fraction in standard form.

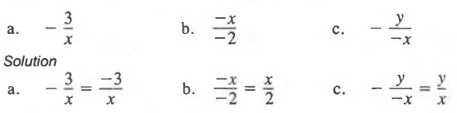
If the numerator contains more than one term, there are alternative standard forms for a fraction.

Example 5 Write in standard form.

Solution Since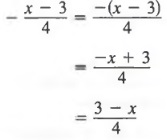

and any of the three forms on the right-hand side of the equals sign may be taken as standard form.

Common Errors When we write a standard form of a fraction such as , we must be careful how we change the signs in the numerator. The use of parentheses helps us avoid errors. Note that in the above example

In particular note that

REDUCING FRACTIONS TO LOWEST TERMS

FUNDAMENTAL PRINCIPLE OF FRACTIONS

In algebra, as in arithmetic, to reduce a fraction to lowest terms, we use the following fundamental principle.

If both the numerator and the denominator of a given fraction are divided by the same nonzero number, the resulting fraction is equivalent to the given fraction.

This fundamental principle is particularly useful in the following form:

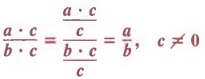
Example 1

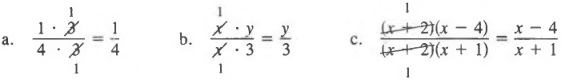
When we reduce fractions, it is easiest to first write the numerator and denominator in factored form and then divide each by their common factors.

Example 2

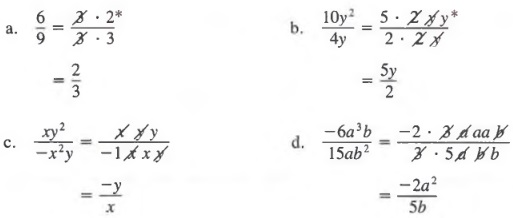
It is critical that when we reduce a fraction in which the numerator and/or the denominator contains more than one term, we must factor wherever possible before applying the fundamental theorem.

Example 3 Reduce

Solution First, we factor the numerators and denominators and then divide out common factors.

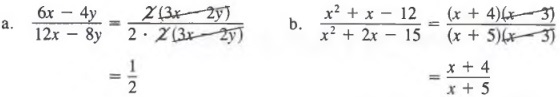
AN ALTERNATE METHOD OF REDUCING FRACTIONS

We have been using the fundamental principle of fractions to reduce fractions. Sometimes, we can reduce fractions by a more direct method.

In cases such as this, where no quotient is indicated above or below the factors "divided out," the quotient 1 is understood.

Consider the quotient

which, in exponential form, is written as a^m-n. Thus,

Example 4

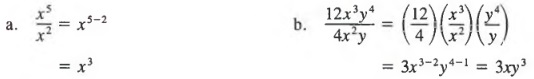
If the greater exponent is in the denominator, that is, if n is greater than m, then

Thus, when we divide powers with the same base, either we can factor each power and divide out common factors or we can use Properties (1) and (2) above.

Example 5 Reduce by
a. Using the fundamental principle of fractions.
b. Using Properties (1) and (2).

Solution

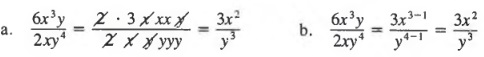
Common Errors: Many errors are made in working with fractions. Careful attention to the following kinds of errors may help you to avoid them. Note that

From the fundamental principle of fractions,

However,

Thus, while we can divide out common factors, we cannot divide out common terms. As another example, note that

From the fundamental principle,

However,

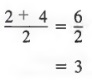
As another example of a common error, note that:

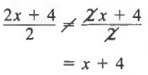
In the expression

we cannot “divide out” the 2’s until we write 2 as a factor of the entire numerator. Thus,

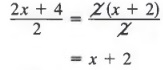
QUOTIENTS OF POLYNOMIALS

MONOMIAL DIVISORS

In Section 5.2 we simplified a quotient by reducing the fraction. In this section, we will study two alternative methods of rewriting quotients in equivalent forms.

We use the first method when the divisor is a monomial. As noted in Section 5.1,

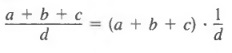
and by the distributive property,

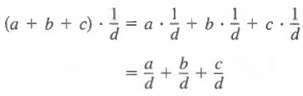
Therefore,

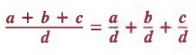
Thus, a fraction whose numerator is a sum or difference of several terms can be expressed as the sum or difference of fractions whose numerators are the terms of the original numerator and whose denominators are the same as the original denominator.

Example 1

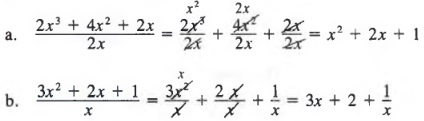
POLYNOMIAL DIVISORS

We use the next method when the divisor is a polynomial. In this case, we use a process similar to arithmetic long division, as the following examples illustrate.

Example 2

As always, the division is not valid if the divisor is 0. Thus, in the example where the divisor is x + 3, we must restrict x from having a value of -3.

When using the long division process, it is convenient to write the dividend in descending powers of the variable. Furthermore, it is helpful to insert a term with a zero coefficient for all powers of the variable that are missing between the highest-degree term and the lowest-degree term.

Example 3 Divide 3x - 1 + 4x³ by 2x - 1.

Solution We first rewrite 3x - 1 + 4x³ as

Now, using the techniques of Example 2, we

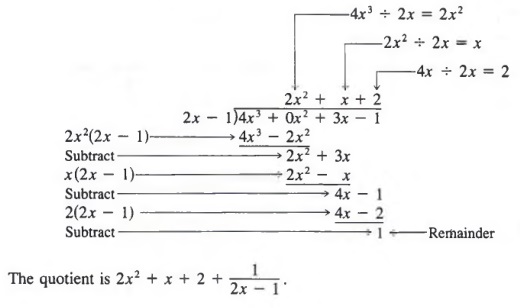
BUILDING FRACTIONS

Just as it is often convenient to reduce fractions to lowest terms, it is also often convenient to build fractions to higher terms. In particular, we will have to build fractions when we add fractions with unlike denominators in the following chapter. In algebra, as in arithmetic, we use the fundamental principle in the following form in order to build fractions.

If both the numerator and denominator of a given fraction are multiplied by the same nonzero number, the resulting fraction is equivalent to the given fraction.

When we apply this principle, we are actually multiplying a quantity by 1 because

To change to a fraction with a denominator bc:

1. Divide b, the denominator of the given fraction, into be, the denominator to be obtained, to find the building factor c.
2. Multiply the numerator and denominator of the given fraction by the building factor c.

Example 1 Express 3/4 as a fraction with a denominator of 8.

Solution We can obtain the building factor by mentally dividing 8 by 4 to get 2 and then we multiply the numerator and denominator by 2 to obtain

The same procedure applies for fractions involving algebraic expressions.

Example 2 Express the first fraction as a fraction with the indicated denominator.

First, we obtain the building factor by dividing x³y² by x²y to get

Then, we can multiply the numerator and denominator of the first fraction by this building factor to obtain

If negative signs are attached to any part of the fraction, it is usually convenient to write the fraction in standard form before building it.

Example 3 Change .

Solution First, we write in standard form and then proceed as in Example 2.

It is helpful, when obtaining the building factor, to first write denominators in factored form.

Example 4 Change .

Solution First, we factor x² - 7x + 12 to get

Next, we obtain the building factor

(x - 3)(x - 4) (x - 3) = (x - 4)

Now, we multiply the numerator and denominator of by the building factor (x - 4), to obtain

INTEGER EXPONENTS; SCIENTIFIC NOTATION

In this section, we will introduce another symbol for a fraction of the form and then we will use this symbol to write certain numbers in simpler form.

INTEGER EXPONENTS

Recall that we have defined a power aⁿ (where n is a natural number) as follows:

aⁿ = a · a · a · · · · · a (n factors)

We will now give meaning to powers in which the exponent is 0 or a negative integer. First, let us consider the quotient a⁴/a⁴. Using the property of quotients of powers, we have

Note that for any a not equal to zero, the left-hand member equals 1 and the right-hand member equals a⁰. In general, we define:

a⁰ = 1

for any number a except 0.

Example 1 a. 3⁰ = 1
b. 425⁰ = 1
c. (x²y)⁰ = 1

Now consider the quotient a⁴/a⁷. Using the two quotient laws for powers, we have

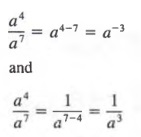
Thus, for any a not equal to 0, we can view a^-3 as equivalent to . In general, we define

for any number a except zero.

Example 2

SCIENTIFIC NOTATION

Very large numbers such as

5,980,000,000,000, 000,000,000,000,000

and very small numbers such as

0.000 000 000 000 000 000 000 001 67

occur in many scientific areas. Large numbers can be rewritten in a more compact and useful form by using powers with positive exponents. We can also rewrite small numbers by using powers with negative exponents that have been introduced in this section.

First, let us consider some factored forms of 38,400 in which one of the factors is a power of 10.

Although any one of such factored forms may be more useful than the original form of the number, a special name is given to the last form. A number expressed as the product of a number between 1 and 10 (including 1) and a power of 10 is said to be in scientific form or scientific notation. For example,

4.18 x 10⁴ , 9.6 x 10², and 4 x 10⁵

are in scientific form.

Now, let us consider some factored forms of 0.0057 in which one of the factors is a power of 10.

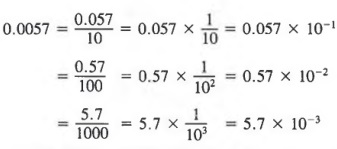
In this case, 5.7 x 10³ is the scientific form for 0.0057.

To write a number in scientific form:

1. Move the decimal point so that there is one nonzero digit to the left of the decimal point.
2. Multiply the result by a power of ten with an exponent equal to the number of places the decimal point was moved. The exponent is positive if the decimal point has been moved to the left and it is negative if the decimal point has been moved to the right.

Example 3

If a number is written in scientific form and we want to rewrite it in standard form, we simply reverse the above procedure.

Example 4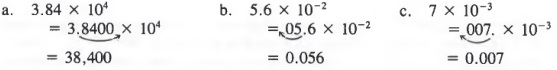

Common Error: Note that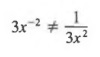

The exponent only applies to the x, not the 3. Thus,

CHAPTER SUMMARY

1. The quotient of two algebraic expressions is called a fraction. We can rewrite a quotient as a product by using the property

   A fraction can be changed from one form to another equivalent form by any of the following properties:

2. We can reduce fractions by using the following principles:

3. A fraction with a monomial denominator can be rewritten as follows:

   A fraction with a denominator that is a polynomial with two or more terms can be rewritten by using a method of long division.

4. We can build fractions by using the fundamental principle

   To change a/b to a fraction with denominator bc:

   1. Divide b into be to obtain the building factor c.
   2. Multiply numerator and denominator of the given fraction by the building factor c.

5. Powers a⁰ and a^-n are defined as follows:

   a⁰ = a (a ≠ 0)

   and

   A number expressed as the product of a number between 1 and 10 (including 1) and a power of 10 is said to be in scientific form or scientific notation. We use scientific notation to rewrite very large and very small numbers.