| f(x) = |
Quadratic Equations
Solving equations is the central theme of algebra. All skills learned lead eventually to the ability to solve equations and simplify the solutions. In previous chapters we have solved equations of the first degree. You now have the necessary skills to solve equations of the second degree, which are known as quadratic equations.
QUADRATICS SOLVED BY FACTORING
OBJECTIVES
Upon completing this section you should be able to:
- Identify a quadratic equation.
- Place a quadratic equation in standard form.
- Solve a quadratic equation by factoring.
A quadratic equation is a polynomial equation that contains the second degree, but no higher degree, of the variable.
The standard form of a quadratic equation is ax2 + bx + c = 0 when a ≠ 0 and a, b, and c are real numbers.
All quadratic equations can be put in standard form, and any equation that can be put in standard form is a quadratic equation. In other words, the standard form represents all quadratic equations.
The solution to an equation is sometimes referred to as the root of the equation.
| This theorem is proved in most college algebra books. |
An important theorem, which cannot be proved at the level of this text, states "Every polynomial equation of degree n has exactly n roots." Using this fact tells us that quadratic equations will always have two solutions. It is possible that the two solutions are equal.
| A quadratic equation will have two solutions because it is of degree two. |
The simplest method of solving quadratics is by factoring. This method cannot always be used, because not all polynomials are factorable, but it is used whenever factoring is possible.
The method of solving by factoring is based on a simple theorem.
If AB = 0, then either A = 0 or B = 0.
| In other words, if the product of two factors is zero, then at least one of the factors is zero. |
We will not attempt to prove this theorem but note carefully what it states. We can never multiply two numbers and obtain an answer of zero unless at least one of the numbers is zero. Of course, both of the numbers can be zero since (0)(0) = 0.
![]()
Solution Step 1 Put the equation in standard form.

| We must subtract 6 from both sides. |
Step 2 Factor completely.
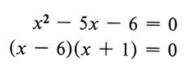
| Recall how to factor trinomials. |
Step 3 Set each factor equal to zero and solve for x. Since we have (x - 6)(x + 1) = 0, we know that x - 6 = 0 or x + 1 = 0, in which case x = 6 or x = - 1.
| This applies the above theorem, which says that at least one of the factors must have a value of zero. |
Step 4 Check the solution in the original equation. If x = 6, then x2 - 5x = 6 becomes
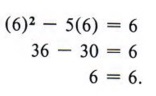
| Checking your solutions is a sure way to tell if you have solved the equation correctly. |
Therefore, x = 6 is a solution. If x = - 1, then x2 - 5x = 6 becomes
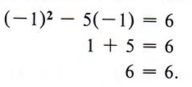
Therefore, - 1 is a solution.
The solutions can be indicated either by writing x = 6 and x = - 1 or by using set notation and writing {6, - 1}, which we read "the solution set for x is 6 and - 1." In this text we will use set notation.
| In this example 6 and -1 are called the elements of the set. |
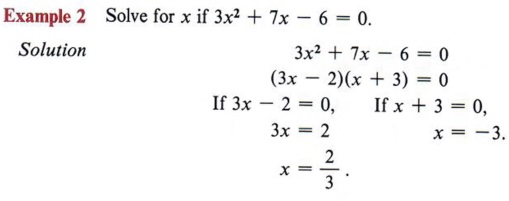
| Note in this example that the equation is already in standard form. |

| Again, checking the solutions will assure you that you did not make an error in solving the equation. |

| (x + 1) is the least common denominator of all the fractions in the equation. Remember, every term of the equation must be multiplied by (x + 1). |
Check the solutions in the original equation.

| Check in the original equation to make sure you do not obtain a denominator with a value of zero. |

| Notice here the two solutions are equal. This only occurs when the trinomial is a perfect square. |
INCOMPLETE QUADRATICS
OBJECTIVES
Upon completing this section you should be able to:
- Identify an incomplete quadratic equation.
- Solve an incomplete quadratic equation.
If, when an equation is placed in standard form ax2 + bx + c = 0, either b = 0 or c = 0, the equation is an incomplete quadratic.
Example 1
5x2 - 10 = 0 is an incomplete quadratic, since the middle term is missing and therefore b = 0.
When you encounter an incomplete quadratic with c - 0 (third term missing), it can still be solved by factoring.
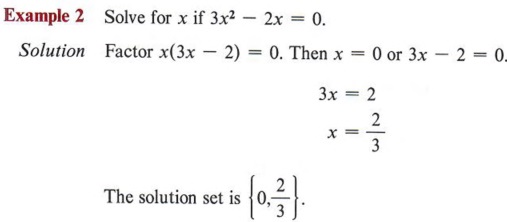
| x is a common factor. The product of two factors is zero. We therefore use the theorem from the previous section. Check these solutions. |
Notice that if the c term is missing, you can always factor x from the other terms. This means that in all such equations, zero will be one of the solutions.
An incomplete quadratic with the b term missing must be solved by another method, since factoring will be possible only in special cases.
Example 3 Solve for x if x2 - 12 = 0.
Solution Since x2 - 12 has no common factor and is not the difference of squares, it cannot be factored into rational factors. But, from previous observations, we have the following theorem.
![]()
| Note that there are two values that when squared will equal A. |
Using this theorem, we have

Check these solutions. |
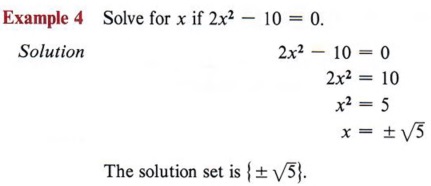
| Add 10 to each side. Check these solutions. |

| Here 7x is a common factor. Check these solutions. |
Note that in this example we have the square of a number equal to a negative number. This can never be true in the real number system and, therefore, we have no real solution.
COMPLETING THE SQUARE
OBJECTIVES
Upon completing this section you should be able to:
- Identify a perfect square trinomial.
- Complete the third term to make a perfect square trinomial.
- Solve a quadratic equation by completing the square.
From your experience in factoring you already realize that not all polynomials are factorable. Therefore, we need a method for solving quadratics that are not factorable. The method needed is called "completing the square."
First let us review the meaning of "perfect square trinomial." When we square a binomial we obtain a perfect square trinomial. The general form is (a + b)2 = a2 + 2ab + b2.
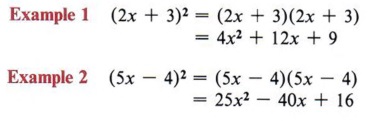
| Remember, squaring a binomial means multiplying it by itself. |
From the general form and these examples we can make the following observations concerning a perfect square trinomial.
- Two of the three terms are perfect squares. 4x2 and 9 in the first example, 25x2 and 16 in the second example, and a2 and b2 in the general form.
In other words, the first and third terms are perfect squares. - The other term is either plus or minus two times the product of the square roots of the other two terms.

The -7 term immediately says this cannot be a perfect square trinomial. The task in completing the square is to find a number to replace the -7 such that there will be a perfect square.
Consider this problem: Fill in the blank so that "x2 + 6x + _______" will be a perfect square trinomial. From the two conditions for a perfect square trinomial we know that the blank must contain a perfect square and that 6x must be twice the product of the square root of x2 and the number in the blank. Since x is already present in 6x and is a square root of x2, then 6 must be twice the square root of the number we place in the blank. In other words, if we first take half of 6 and then square that result, we will obtain the necessary number for the blank.
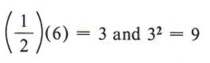
Therefore x2 + 6x + 9 is a perfect square trinomial.
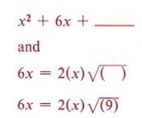

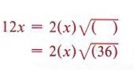
Now let's consider how we can use completing the square to solve quadratic equations.
Example 5 Solve x2 + 6x - 7 = 0 by completing the square.
| Recall that instead of -7, a +9 would make the expression a perfect square. |
Solution First we notice that the -7 term must be replaced if we are to have a perfect square trinomial, so we will rewrite the equation, leaving a blank for the needed number.
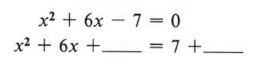
At this point, be careful not to violate any rules of algebra. For instance, note that the second form came from adding +7 to both sides of the equation. Never add something to one side without adding the same thing to the other side.
Now we find half of 6 = 3 and 32 = 9, to give us the number for the blank. Again, if we place a 9 in the blank we must also add 9 to the right side as well.
![]()
| Remember, if 9 is added to the left side of the equation, it must also be added to the right side. |
Now factor the perfect square trinomial, which gives
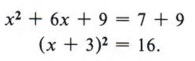
| Now x2 + 6x + 9 may be written as (x + 3)2. |

| Add - 3 to both sides. |
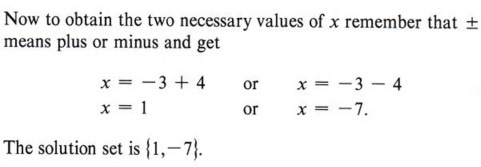
| Thus, 1 and -7 are solutions or roots of the equation. |
Example 6 Solve 2x2 + 12x - 4 = 0 by completing the square.
Solution This problem brings in another difficulty. The first term, 2x2, is not a perfect square.
We will correct this by dividing all terms of the equation by 2 and obtain

| In other words, obtain a coefficient of 1 for the x2 term. |
We now add 2 to both sides, giving

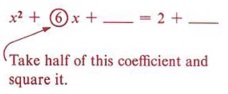 Again, this is more concise. |
Example 7 Solve 3x2 + 7x - 9 = 0 by completing the square.
Solution Step 1 Divide all terms by 3.

| Again, obtain a coefficient of 1 for x2 by dividing by 3. |
Step 2 Rewrite the equation, leaving a blank for the term necessary to complete the square.
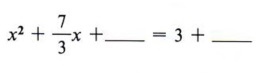

Step 3 Find the square of half of the coefficient of x and add to both sides.
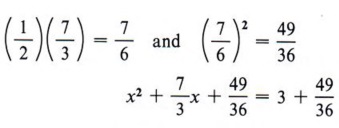
| It looks complex, but we are following the same exact rules as before. |
Step 4 Factor the completed square.
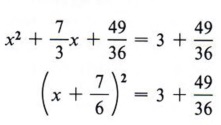
The factoring should never be a problem since we know we have a perfect square trinomial, which means we find the square roots of the first and third terms and use the sign of the middle term.
You should review the arithmetic involved in adding the numbers on the right at this time if you have any difficulty.
We now have 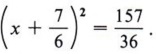
Step 5 Take the square root of each side of the equation.
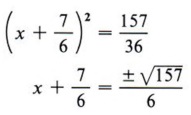
Step 6 Solve for x (two values).
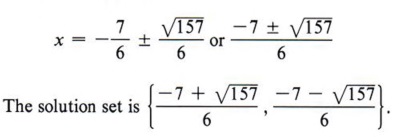


Follow the steps in the previous computation and then note especially the last ine. What is the conclusion when the square of a quantity is equal to a negative number? "No real solution."
| What real number can we square and obtain -7? |
In summary, to solve a quadratic equation by completing the square, follow this step-by-step method.
Step 1 If the coefficient of x2 is not 1, divide all terms by that coefficient.
Step 2 Rewrite the equation in the form of x2 + bx + _______ = c + _______.
Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation.
Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation.
Step 5 Find the square root of each side of the equation.
Step 6 Solve for x and simplify.
If step 5 is not possible, then the equation has no real solution.
| These steps will help in solving the equations in the following exercise. |
THE QUADRATIC FORMULA
OBJECTIVES
Upon completing this section you should be able to:
- Solve the general quadratic equation by completing the square.
- Solve any quadratic equation by using the quadratic formula.
- Solve a quadratic equation by completing the square.
The standard form of a quadratic equation is ax2 + bx + c = 0. This means that every quadratic equation can be put in this form. In a sense then ax2 + bx + c = 0 represents all quadratics. If you can solve this equation, you will have the solution to all quadratic equations.
We will solve the general quadratic equation by the method of completing the square.
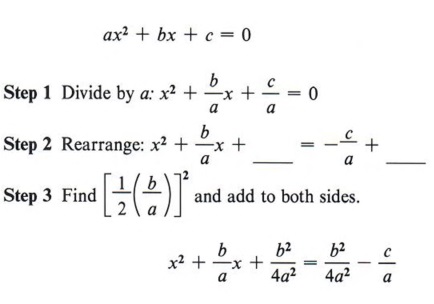
| This is to obtain an x2 term with a coefficient of 1. This we did in the previous section many times. |

| We must add |
This form 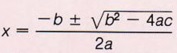 is called the quadratic formula and represents the solution to all quadratic equations.
is called the quadratic formula and represents the solution to all quadratic equations.
| Memorize this expression. |
To use the quadratic formula you must identify a, b, and c. To do this the given equation must always be placed in standard form.

| Carefully substitute the values of a, b, and c in the formula. |

Not every quadratic equation will have a real solution.
| This equation is already in standard form. |
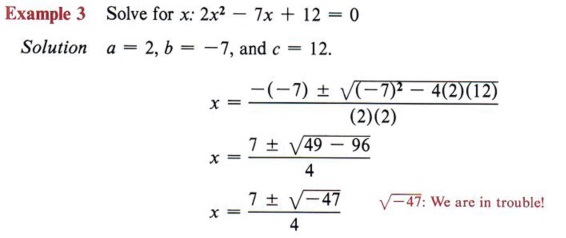
There is no real solution since -47 has no real square root.
| Again, this equation is in standard form. |
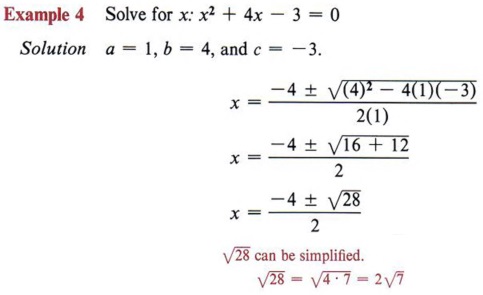
This solution should now be simplified.

WORD PROBLEMS
OBJECTIVES
Upon completing this section you should be able to:
- Identify word problems that require a quadratic equation for their solution.
- Solve word problems involving quadratic equations.
Certain types of word problems can be solved by quadratic equations. The process of outlining and setting up the problem is the same as taught in chapter 5, but with problems solved by quadratics you must be very careful to check the solutions in the problem itself. The physical restrictions within the problem can eliminate one or both of the solutions.
Example 1 If the length of a rectangle is 1 unit more than twice the width, and the area is 55 square units, find the length and width.
Solution The formula for the area of a rectangle is Area = Length X Width. Let x = width, 2x + 1 = length.
| If x represents the width, then 2x represents twice the width and 2x + 1 represents one more than twice the width. |

| Place the quadratic equation in standard form. This quadratic can be solved by factoring. |
At this point, you can see that the solution x = -11/2 is not valid since x represents a measurement of the width and negative numbers are not used for such measurements. Therefore, the solution is
width = x = 5, length = 2x + 1 = 11.
| A measurement cannot be a negative value. |

| The reciprocal of x is Remember LCD means lowest common denominator. Every term must be multiplied by 10x. Again, this quadratic can be factored. |
Both solutions check. Therefore, the solution set is 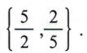 .
.
| There are two solutions to this problem. |
Example 3 If a certain integer is subtracted from 6 times its square, the result is 15. Find the integer.
Solution Let x = the integer. Then

Since neither solution is an integer, the problem has no solution.
| You might be tempted to give these values as a solution unless you paid close attention to the fact that the problem asked for an integer. |
Example 4 A farm manager has 200 meters of fence on hand and wishes to enclose a rectangular field so that it will contain 2,400 square meters in area. What should the dimensions of the field be?
Solution Here there are two formulas involved. P = 2l + 2w for the perimeter and A = lw for the area.
First using P = 2l + 2w, we get

| Divide each term by 2. |
We can now use the formula A = lw and substitute (100 - l) for w, giving
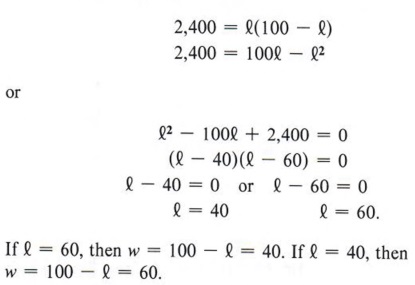
The field must be 40 meters wide by 60 meters long.
We could just as well solve for l obtaining l = 100 - w. Then |
Note that in this problem we actually use a system of equations
P = 2 l + 2 w
A = l w.
In general, a system of equations in which a quadratic is involved will be solved by the substitution method. (See chapter 6.)
SUMMARY
Key Words
- A quadratic equation is a polynomial equation in one unknown that contains the second degree, but no higher degree, of the variable.
- The standard form of a quadratic equation is ax2 + bx + c = 0, when a ≠ 0.
- An incomplete quadratic equation is of the form ax2 + bx + c = 0, and either b = 0 or c = 0.
- The quadratic formula is
![]()
Procedures
- The most direct and generally easiest method of finding the solutions to a quadratic equation is factoring. This method is based on the theorem: if AB = 0, then A = 0 or B = 0. To use this theorem we put the equation in standard form, factor, and set each factor equal to zero.
- To solve a quadratic equation by completing the square, follow these steps:
Step 1 If the coefficient of x2 is not 1, divide all terms by that coefficient.
Step 2 Rewrite the equation in the form of x2 + bx +_____ = c + _____
Step 3 Find the square of one-half of the coefficient of the x term and add this quantity to both sides of the equation.
Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation.
Step 5 Find the square root of each side of the equation.
Step 6 Solve for x and simplify. - The method of completing the square is used to derive the quadratic formula.
- To use the quadratic formula write the equation in standard form, identify a, b, and c, and substitute these values into the formula. All solutions should be simplified.
