THE INTEGERS, SIGNED NUMBERS AND NUMERICAL FRACTIONS

INTEGERS AND THEIR GRAPHS

INTEGERS

On occasion, we use natural numbers to represent physical quantities such as money (5 dollars), temperature (20 degrees), and distance (10 miles). Since this representation does not differentiate between gains and losses, degrees above or below zero, or distances in opposite directions from a starting point, mathematicians have found it convenient to represent these ideas symbolically by the use of plus (+) and minus (-) signs. For example, we may represent

A loss of five dollars as -$5.
A gain of five dollars as +$5.
Ten degrees below zero as -10°.
Ten degrees above zero as +10°.
Ten miles to the west of a starting point as -10 miles.
Ten miles to the east of a starting point as +10 miles.

Nonzero numbers that are preceded by a minus sign are called negative numbers. Nonzero numbers that are preceded by a plus sign are called positive numbers. Together these numbers are called signed numbers. Note that zero is not considered positive or negative.

The signed numbers, together with zero,

. . . , -3, -2, -1, 0, +1, +2, +3, . . .

are called integers. When a numeral is written without a sign, for example, 3, 5, 9, we assume that a plus sign is intended.

We refer to the numbers

. . . , -6, -4, -2, 0, 2, 4, 6, . . .

as even integers. And we refer to the numbers

. . . , -5, -3, -1, 1, 3, 5, . . .

as odd integers.

Note that even integers are multiples of 2. An integer is odd if it leaves a remainder of 1 when it is divided by 2.

ORDER OF INTEGERS

The number line used to represent whole numbers can be extended to the left of the origin to include the graphs of negative numbers, as shown in Figure 2.1

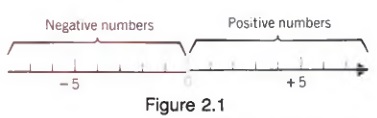
Example 1 Graph the numbers on a number line.

a. -5, -3, -2, -1, 0, 3
b. The odd integers between -5 and 7.

Solutions

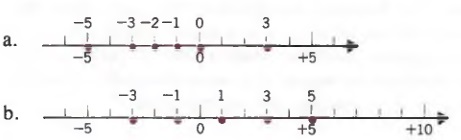
As before, the number line is particularly useful in visualizing the relative order of two numbers.

An integer whose graph lies to the left of the graph of a second integer is less than the second integer.

Example 2 Replace the comma in each pair with the proper symbol: < or > .

a. -3,3
b. -1,0
c. -2,-5
d. 0,-2

Solutions

Referring to the graph in Example la, we get

a. -3 < 3, read "negative three is less than three";
b. - 1 < 0, read "negative 1 is less than zero";
c. - 2 > -5, read "negative two is greater than negative five";
d. 0 > -2, read "zero is greater than negative two."

This notion of the order of integers is consistent with our physical experiences. A temperature of -5° is lower or less than one of -2°, -3° is less than 3°, and -1° is less than 0°.

THE SYMBOL " - "

We have now used the symbol "-" to indicate a sign of operation (subtraction) and to indicate negative numbers. We also use the symbol " to mean the "opposite" or "negative" of a number.

-x means the "opposite" of x.

If x is positive, then -x is negative. For example,

-(5) = -5 and -(10) = -10

If x is negative, then - x is positive. For example,

-(-5) = +5 and -(-10) = +10

For any a, positive or negative, the opposite of the opposite of a is a. In symbols we write

-(-a) = a

ABSOLUTE VALUE

The absolute value of a signed number is the value of the number without regard to its sign. We can think of a signed number as having two parts: the sign of the number and the absolute value of the number. When no sign is written, we assume that the sign is positive. For example,

In the case of 0, we define the absolute value of zero to be zero. Thus, the absolute value of any integer is never negative.

We designate absolute value by vertical bars.

Example 3 Simplify.

a. | -5 |
b. | 7 |
c. | 0 |

Solution

a. | -5 | = 5, read "the absolute value of negative five is equal to five";
b. | 7 | = 7, read "the absolute value of seven is equal to 7";
c. | 0 | = 0, read "the absolute value of zero is equal to zero."

We define the absolute value of x more formally as

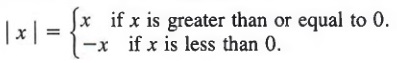
Example 4
a. | 3 | = 3, | 5 | = 5, and | 0 | = 0. In this case, 3, 5, and 0 are greater than or equal to 0. Thus, the absolute value is the number itself.
b. | -3 | = -(-3) = 3 and | -5 | = -(-5) = 5. In this case, -3 and -5 are less than 0. So we take the negative of -3 and the negative of -5 to find the absolute value.

SUMS OF INTEGERS

To see what is meant by the sum of two signed numbers, we can think of such numbers as representing gains and losses, (+) numbers denoting gains and (-) numbers denoting losses.

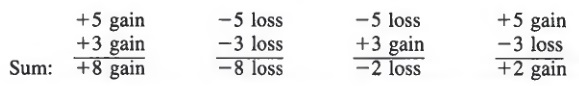
In algebra, we usually write sums horizontally. Thus, we would write the sum of +5 and +3 as

+5 + (+3) - +8 or 5 + 3 = 8

And we would write the sum of -5 and -3 as

-5 + (-3) = -8

For the sum of -5 and +3, we would have

-5 + (+3) = -2 or -5 + 3 = -2

and for the sum of +5 and -3,

+5 + (-3) = 2 or 5 + (-3) = 2

The above examples suggest a rule for the addition of integers.

To add integers with like signs:

1. Add the absolute values of the numbers.
2. The sum has the same sign as the numbers.

To add integers with unlike signs:

1. Find the absolute value of each and subtract the lesser absolute value from the greater absolute value.
2. The sum has the same sign as the number with the greater absolute value.

Example 1 Add

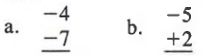
Solutions

a. Since the signs are alike, add the absolute values.
| 4 | + | -7 | = 4 + 7 = 11
The sum has the same sign as the numbers, -4 and -7.
Ans. -11

b. Since the signs are unlike, subtract the lesser absolute value from the greater absolute value.
| -5 | = 5 ; | +2 | = 2; 5 - 2 = 3
Since | -5 | is greater than | +2 |, the sum is negative.
Ans. -3

Example 2 Add

a. (-5) +(-7)
b. (+6) + (-2)

Solutions

a. Since the signs are alike, add the absolute values.
| -5 | + | -7 | = 5 + 7 = 12
The sum has the same sign as the numbers, -5 and -7.
Ans. -12

b. Since the signs are unlike, subtract the lesser absolute value from the greater absolute value.
| +6 | = 6; | -2 | = 2; 6 - 2 = 4
Since | +6 | is greater than | -2 |, the sum is positive.
Ans. +4 or 4

Example 3

We assume that the commutative and associative laws of addition hold with respect to integers. For example,

2 + (-3) = -3 + 2

and

[2 + (-3)] + 4 = 2 + [(-3) + 4]

SUMS INVOLVING VARIABLES

In Chapter 1, we combined like algebraic terms by adding their numerical coefficients. Now we can rewrite sums of terms with positive or negative coefficients according to the laws of signs in Section 2.2.

Example 1 Simplify.

Solutions

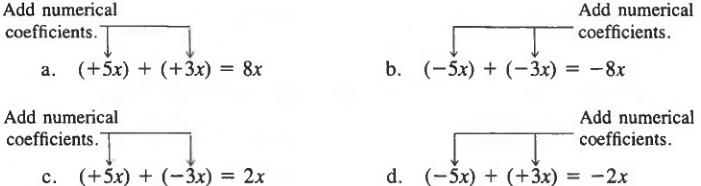
If a variable is preceded by a minus sign, the coefficient -1 is understood. Thus,

-x = -1·x

-x² = -1 · x²

and so on.

Example 2

As in Section 2.2, it is convenient to rewrite sums that involve parentheses without using parentheses. We can therefore write (+5x) + (+3x) simply as 5x + 3x. In general,

a + (+b) = a + b

We can extend this idea to expressions in which two or more terms are grouped by parentheses.

In expressions involving only addition, parentheses that are preceded by a plus sign may be dropped; each term within the parentheses keeps its original sign.

Thus,

x + (y + z) = x + y + z

Example 3

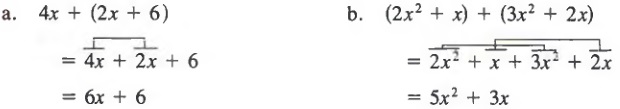
DIFFERENCES OF INTEGERS

When we discussed the difference of two natural numbers in Section 1.2, we saw that 5 - 3 is a number 2 that, when added to 3, gives 5. In general, a - b is a number that, when added to b, gives a. The same idea holds for the difference of two integers. For example,

(+5) - (+2) = (+3) because (+2) + (+3) = (+5)

Now, since

(+5) + (-2) = (+3)

we have

(+5) - (+2) = (+5) + (-2)

This and similar examples suggest the following rule.

To subtract an integer b from an integer a:

1. Change the subtraction to addition.
2. Change the sign of b.
3. Proceed as in addition.

In symbols,

a - b = a + (-b)

We can now view an expression such as 5 - 2 as the difference (+5) - (+2) or as the sum (+5) + (-2). In either case,the expression equals 3. Similarly, 2 - 5 can be viewed as the difference (+2) - (+5) or as the sum (+2) + (-5), where both expressions are equal -3. Because it is easier to work with sums, we usually rewrite a difference as a sum, and then add.

Example 1 Find each difference.

Solutions

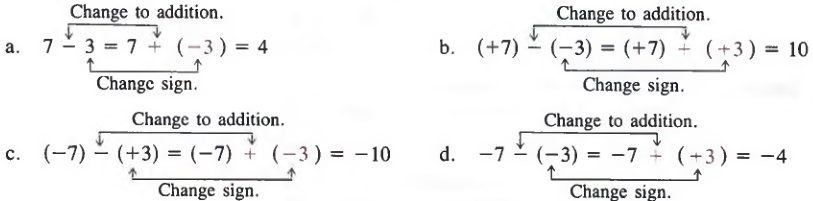
We can also write a difference as a sum in expressions that contain more than two terms.

Example 2

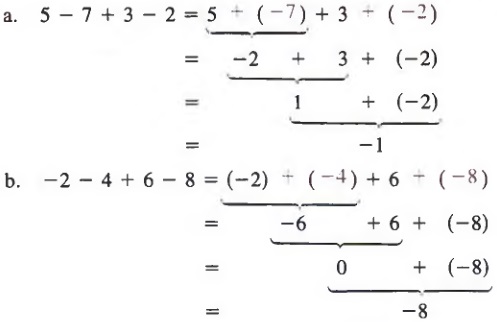
When more than two terms are involved, we can use the commutative and associative laws to help us rewrite sums or differences by grouping the positive terms and grouping the negative terms. Thus, the examples above could be simplified as follows.

Example 3

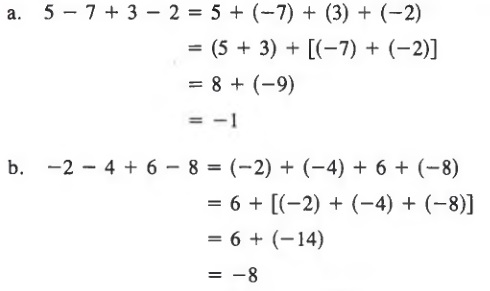
Note that each minus sign in the expression 5 - 7 + 3 - 2 can be viewed as the sign associated with the number that follows, while the operation is understood to be addition.

We can also find the difference between two integers written in vertical form by changing the sign on the number being subtracted and then adding the two numbers.

Example 4 Subtract the bottom number from the top number.

Solutions

DIFFERENCES INVOLVING VARIABLES

In Section 2.3 we rewrote sums of algebraic expressions by adding the numerical coefficients of like terms. Using a similar method, we can also rewrite differences in which the terms of the expression have positive or negative coefficients.

Example 1

We can also rewrite as sums those differences that do not involve parentheses.

Example 2

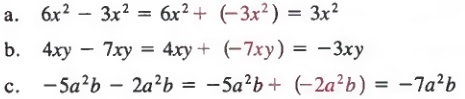
In any expression that contains some like terms and some unlike terms, we can also rewrite the expression so that all the operations involved are additions.

Example 3

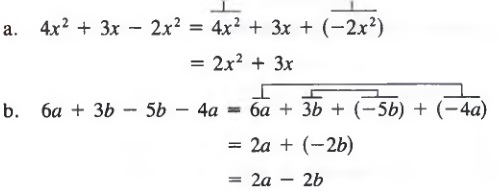
We must be careful when removing parentheses preceded by a minus sign. For example, to rewrite

(+5x - 2y) - (+7x - 4y)

without parentheses, we must remember that the minus sign applies to the entire binomial (+7x - 4y). Therefore, we must change the sign of each term in (+7x - 4y). Since +7x - 4y is the same as +7x + (-4y), changing the signs yields -7x + (+4y) and we get

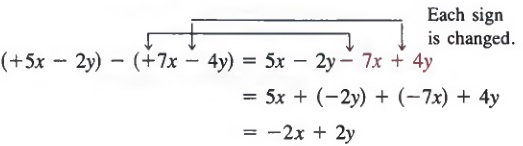
As a general rule,

If an expression is inside parentheses preceded by a minus sign, the sign of each term is changed when the expression is written without parentheses.

Example 4

We can also use a vertical format to subtract polynomials. Again, we must be careful to properly change signs.

Example 5 Subtract the bottom polynomial from the top polynomial.

Common Errors: Many errors occur when differences are involved. You must be careful to change signs properly. For example,

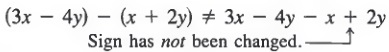
and

PRODUCTS

You may recall that multiplication is a form of addition. That is, we can think of 3(2) as the sum of three 2's (2 + 2 + 2), and we can think of 3(-2) as the sum of three -2's [(-2) + (-2) + (-2)], which is -6. Thus, it would appear that the product of a positive and negative number should be a negative number.

Now let us investigate the product of two negative numbers. First, consider the following sequence of products:

4(-2) = -8

3(-2) = -6

2(-2) = -4

1(-2) = -2

0(-2) = 0

If we continue the sequence with the product - 1 (-2), it seems plausible (from the sequence above) that the number 2 is the next number in the sequence following the equals sign. That is, the sequence continues with

-1(-2) = 2

-2(-2) = 4

-3(-2) = 6

and so on. It appears (at least intuitively) that the product of two negative numbers is a positive number. In fact, this is the case and we adopt the following rule.

To find the product of two signed numbers:

1. Multiply the absolute value of the numbers.
2. Determine the sign of the product:
   if the factors have like signs, the product is positive;
   if the factors have unlike signs, the product is negative.

In symbols,

(+a)(+b) = +(ab),
(-a)(-b) = +(ab),
(+a)(-b) = -(ab) and
(-a)(+b) = -(ab)

Also, the product of zero and any integer is zero.

Example 1

Again, we assume that the commutative and associative laws of mulitplication hold for signed numbers. For example, by the commutative law,

(2)(3) = 3(-2)

And by the associative law,

[(-2)(3)](4) = (2)[(3)(4)]

We can determine the sign of the product of any number of factors. If we have an odd number of negative factors, the product is negative; if we have an even number of negative factors, the product is positive.

Example 2

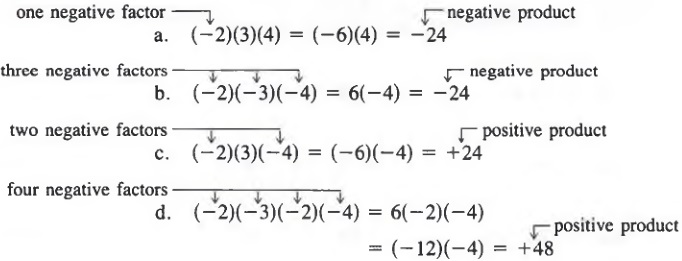
Using the rules of signs for multiplying integers, we can now find products of monomials with positive or negative coefficients.

Example 3

Common Error: On page 56, we noted that

-x = -1·x
-x² = -1·x²

and so on. Thus,

-3² = - 1·3² = -9

On the other hand,

(-3)² = (-3)(-3) = 9

Thus, -3² ≠ (-3)². In general,

-x² ≠ (-x)²

Example 4

QUOTIENTS

We define the quotient of two integers the same way we define the quotient of two natural numbers (Section 1.3). However, the sign of the quotient has to be consistent with the rule of signs for the multiplication of signed numbers. Recall that for natural numbers, the quotient a/b is the number q such that b · q = a. Let us examine the quotient of two signed numbers by considering some numerical cases.

These examples suggest the following rule.

To find the quotient of two signed numbers:

1. Find the quotient of the absolute values of the numbers.
2. Determine the sign of the quotient:
   if the dividend and divisor have like signs, the quotient is positive;
   if the dividend and divisor have unlike signs, the quotient is negative.

In symbols:

QUOTIENTS INVOLVING ZERO

As for whole numbers, a quotient equals zero if the dividend is zero and the divisor is not zero. And as always, division by 0 is undefined. For example,

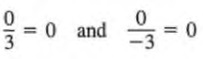
whereas

Example 1

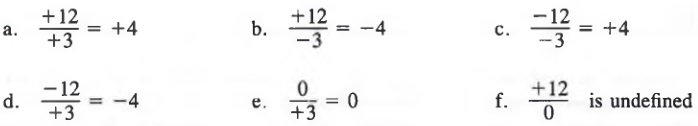
QUOTIENTS OF MONOMIALS

Using the rules of signs for quotients of integers, we can find quotients of monomials with positive or negative coefficients.

Exampie 2 Simplify

Solutions
We can divide the numerical factors and divide out common factors.

For more complicated expressions, we follow the order of operations from Section 1.5.

Example 3 Simplify

Solution We first simplify above the fraction bar to obtain

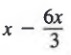
Now, we simplify the quotient and subtract

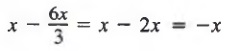
NUMERICAL EVALUATION

We can evaluate expressions using integers in the same way we evaluate expressions using natural numbers (see Section 1.6). It is helpful to use parentheses (as in the following examples) each time a substitution is made. Furthermore, the order for performing operations discussed in Section 1.5 is also valid for integers and should be followed carefully.

Example 1 Evaluate 3x² + 2x - 3 for x = -3.

Solution We first substitute -3 for x, using parentheses to avoid sign mistakes, and obtain

3(-3)² + 2(-3) - 3

Now, we evaluate powers and multiply to get

3(9) + 2(-3) - 3 = 27 + (-6) - 3

Last, we add or subtract to obtain

27 + (-6) - 3 = 18

Example 2 Evaluate 3x² - xy + 2y² for x = 2, y = -1.

Solution We first substitute 2 for x and -1 for y to obtain

3(2)² - (2)(-l) + 2(-1)²

Now, we evaluate powers and multiply to get

3(4) - (2)(- 1) + 2(1) = 12 - (-2) + 2

Last, we add or subtract to obtain

12 - (-2) + 2 = 16

SPECIAL NOTATION

In Section 1.7 we defined polynomials. Polynomials are frequently represented by expressions such as P(x), D(y), and Q(z), where the symbol in parentheses designates the variable. These symbols are read "P of x," "D of y," and "Q of z," respectively. For example, we might write

P{x) = x² - 2x + 1
D(y) = y⁶ -2y² + 3y - 2
Q(z) = 8z⁴ + 3z³ - 2z² + z - 1

We can use this notation to represent values of the polynomial for specific values of the variable. Thus, we write P(2) to represent the value of P(x) when x is replaced by 2. Therefore, to evaluate P (2), we first replace x with 2 and then follow the proper order of operations.

Example 3 For P(x) = x² - 2x + 1, find
a. P(2)
b. P(-4)

Solutions
a. First, we replace x by 2 to obtain

P(2) = (2)² - 2(2) + 1

Now, following our order of operations yields

P(2) = 4 - 4 + 1 = 1

b. First, we replace x by -4 to obtain

P(-4) = (-4)² - 2(-4) + 1

Now, following our order of operations yields

P(-4) = 16 + 8 + 1 = 25

CHAPTER SUMMARY

1. The numbers

   . . . , -3, -2, -1, 0, +1, +2, +3, . . .

   are called integers. On a number line, an integer whose graph lies to the left of the graph of a second integer is less than the second integer.

   The absolute value of an integer is the value of the integer without regard to its sign.

2. To add two integers with like signs,

   1. Add the absolute values of the numbers.
   2. The sum has the same sign as the numbers.

   To add two integers with unlike signs,

   1. Find the absolute value of each and subtract the lesser absolute value from the greater absolute value.
   2. The sum has the same sign as the number with the greater absolute value.

   In expressions involving only addition, parentheses that are preceded by a plus sign may be dropped; each term within the parentheses retains its original sign.

3. To subtract an integer b from an integer a, change the sign of b and add the two integers.

   a - b = a + (-b)

   In expressions involving addition and subtraction, parentheses preceded by a minus sign may be dropped, provided the sign of each term inside the parentheses is changed when the expression is written without parentheses.

4. To find the product of two integers, multiply the absolute values of the numbers. If the factors have like signs, the product is positive; if the factors have unlike signs, the product is negative. If one of the factors is zero, the product is zero.

5. To find the quotient of two signed numbers, find the quotient of the absolute values of the numbers. If the dividend and divisor have like signs, the quotient is positive; if the dividend and divisor have unlike signs, the quotient is negative. If zero is divided by any nonzero number, the quotient is zero. Division by 0 is undefined.

6. To evaluate an expression for given numbers, substitute the given number(s) for the variable(s) and follow the correct order of operations.