MULTIPLICATIVE INVERSES OF MATRICES

In this section multiplicative identity elements and multiplicative inverses are introduced and used to solve matrix equations. This leads to another method for solving systems of equations.

IDENTITY MATRICES The identity property for real numbers says that a * I = a and I * a = a for any real number a. If there is to be a multiplicative identity matrix I, such that:

 AI = A and  IA = A,

for any matrix A, then A and I must be square matrices of the same size. Otherwise it would not be possible to find both products. For example, let A be the 2 X 2 matrix and let

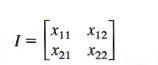
represent the 2 X 2 identity matrix. To find I, use the fact that IA = A, or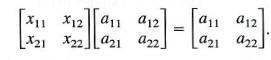



Multiplying the two matrices on the left side of this equation and setting the elements of the product matrix equal to the corresponding elements of A gives the following system of equations with variables x11, x12, x21, and x22

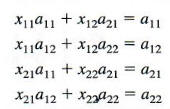
Notice that this is really two systems of equations in two variables. Use one of the methods of the previous chapter to find the solution of this system: x11 = 1, x12 = x21 = 0, and X22 = 1. From the solution of the system, the 2 X 2 identity matrix is

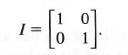
Check that with this definition of I, both Al = A and IA = A.
 

Example 1 VERIFYING THE IDENTITY PROPERTY

Let

Verify that MI = M and IM = M

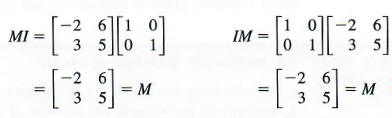
The 2 X 2 identity matrix found above suggests the following generalization:

n x n IDENTITY MATRIX

For any value of n there is an n X n identity matrix having l's down the diagonal and 0's elsewhere. The n x n identity matrix is given by l where:

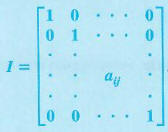
Here aij = 1 when i = j (the diagonal elements) and aaj = 0 otherwise.

Example 2 - STATING AND VERIFYING THE 3 X 3 IDENTITY MATRIX

Let K =

Given the 3 X 3 identity matrix I and show that KI = K.

The 3 X 3 identity matrix is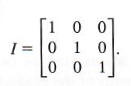

By the definition of matrix multiplication,
 

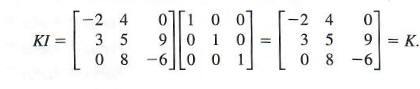
MULTIPLICATIVE INVERSES For every nonzero real number a, there is a multiplicative inverse l/a such that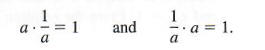

Recall that l/a can also be written a^(-1). In the rest of this section, a method is developed for finding a multiplicative inverse for square matrices. The multiplicative inverse of a matrix A is written A^(-1). This matrix must satisfy the statements

The multiplicative inverse of a matrix can be found using the matrix row transformations given in the previous tutorial and repeated here for convenience.

MATRIX ROW TRANSFORMATIONS

The matrix row transformations are:

1. interchanging any two rows of a matrix;

2. multiplying the elements of any row of a matrix by the same nonzero scalar k; and

3. adding a multiple of the elements of one row to the elements of another row.
   

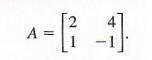
Let the unknown inverse matrix be

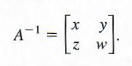
By the definition of matrix inverse, AA^(-1) = 1, or

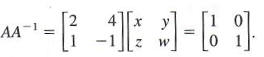
By matrix multiplication,

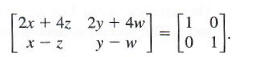
Setting corresponding elements equal gives the system of equations

Since equations (1) and (3) involve only x and z, while equations (2) and (4) involve only y and w, these four equations lead to two systems of equations,

2x + 4z = 1
x-z=0

and

2y + 4w = 0
y-w=1.

Writing the two systems as augmented matrices gives

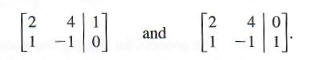
Each of these systems can be solved by the Gauss-Jordan method. However, since the elements to the left of the vertical bar are identical, the two systems can be combined into the one augmented matrix,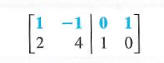

and solved simultaneously as follows. Exchange the two rows to get a 1 in the upper left comer.

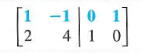
Multiply the first row by -2 and add the results to the second row to get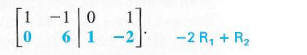


Now, to get a I in the second-row, second-column position, multiply the second row by 1/6.

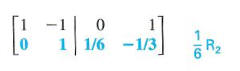
Finally, add the second row to the first row to get a 0 in the second column above the 1.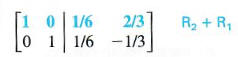

The numbers in the first column to the right of the vertical bar give the values of x and z. The second column gives the values of y and w. That is,

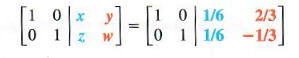
so that

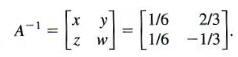
To check, multiply A by A^(-1). The result should be I

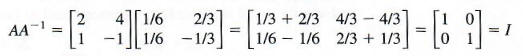
Verify that A - 1 A = I, also. Finally,

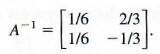
The process for finding the multiplicative inverse A^(-1) n x n matrix A that has an inverse is summarized below.

FINDING AN INVERSE MATRIX
To obtain A^(-1) n x n matrix A for which A^(-1) exists, follow these steps.

1. Form the augmented matrix [A/I], where I is the n x n identity matrix.
2. Perform row transformations on [A|I] to get a matrix of the form [I|B].
3. Matrix B is A^(-1).
4. Verify by showing that BA = AB = I.

CAUTION Only square matrices have inverses, but not every square matrix has an inverse. If an inverse exists, it is unique. That is, any given square matrix has no more than one inverse. Note that the symbol A^(-1) does not mean 1/A; the symbol A^(-1) is just the notation for the inverse of matrix A.