Solving Equations
The solution of equations is the central theme of algebra. In this chapter we will study some techniques for solving equations having one variable. To accomplish this we will use the skills learned while manipulating the numbers and symbols of algebra as well as the operations on whole numbers, decimals, and fractions that you learned in arithmetics.
CONDITIONAL AND EQUIVALENT EQUATIONS
OBJECTIVES
Upon completing this section you should be able to:
- Classify an equation as conditional or an identity.
- Solve simple equations mentally.
- Determine if certain equations are equivalent.
An equation is a statement in symbols that two number expressions are equal.
Equations can be classified in two main types:
1. An identity is true for all values of the literal and arithmetical numbers in it.
Example 1 5 x 4 = 20 is an identity.
Example 2 2 + 3 = 5 is an identity.
Example 3 2x + 3x = 5x is an identity since any value substituted for x will yield an equality.
2. A conditional equation is true for only certain values of the literal numbers in it.
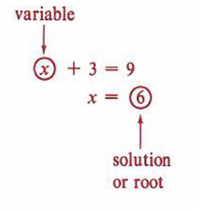
Example 4 x + 3 = 9 is true only if the literal number x = 6.
Example 5 3x - 4 = 11 is true only if x = 5.
The literal numbers in an equation are sometimes referred to as variables.
Finding the values that make a conditional equation true is one of the main objectives of this text.
A solution or root of an equation is the value of the variable or variables that make the equation a true statement.
The solution or root is said to satisfy the equation.
Solving an equation means finding the solution or root.
Many equations can be solved mentally. Ability to solve an equation mentally will depend on the ability to manipulate the numbers of arithmetic. The better you know the facts of multiplication and addition, the more adept you will be at mentally solving equations.
Example 6 Solve for x: x + 3 = 7
Solution
To have a true statement we need a value for x that, when added to 3, will yield 7. Our knowledge of arithmetic indicates that 4 is the needed value. Therefore the solution to the equation is x = 4.
| What number added to 3 equals 7? |
Example 7 Solve for x: x - 5 = 3
Solution
What number do we subtract 5 from to obtain 3? Again our experience with arithmetic tells us that 8 - 5 = 3. Therefore the solution is x = 8.
Example 8 Solve for x: 3x = 15
Solution
What number must be multiplied by 3 to obtain 15? Our answer is x = 5.
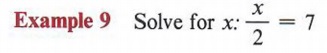
Solution
What number do we divide 2 by to obtain 7? Our answer is 14.
Example 10 Solve for x: 2x - 1 = 5
Solution
We would subtract 1 from 6 to obtain 5. Thus 2x = 6. Then x = 3.
Regardless of how an equation is solved, the solution should always be checked for correctness.
Example 11 A student solved the equation 5x - 3 = 4x + 2 and found an answer of x = 6. Was this right or wrong?
Solution
Does x = 6 satisfy the equation 5x - 3 = 4x + 2? To check we substitute 6 for x in the equation to see if we obtain a true statement.
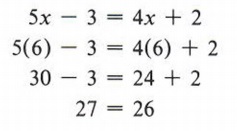
This is not a true statement, so the answer x = 6 is wrong.
Another student solved the same equation and found x = 5.
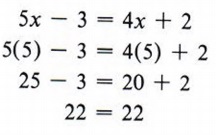
This is a true statement, so x = 5 is correct.
| Many students think that when they have found the solution to an equation, the problem is finished. Not so! The final step should always be to check the solution. |
Not all equations can be solved mentally. We now wish to introduce an idea that is a step toward an orderly process for solving equations.
| Is x = 3 a solution of x - 1 = 2? Is x = 3 a solution of 2x + I = 7? What can be said about the equations x - 1 = 2 and 2x + 1 = 7? |
Two equations are equivalent if they have the same solution or solutions
Example 12 3x = 6 and 2x + 1 = 5 are equivalent because in both cases x = 2 is a solution.
Techniques for solving equations will involve processes for changing an equation to an equivalent equation. If a complicated equation such as 2x - 4 + 3x = 7x + 2 - 4x can be changed to a simple equation x = 3, and the equation x = 3 is equivalent to the original equation, then we have solved the equation.
Two questions now become very important.
- Are two equations equivalent?
- How can we change an equation to another equation that is equivalent to it?
The answer to the first question is found by using the substitution principle.
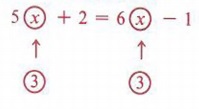
Example 13 Are 5x + 2 = 6x - 1 and x = 3 equivalent equations?
Solution

The answer to the second question involves the techniques for solving equations that will be discussed in the next few sections.
| To use the substitution principle correctly we must substitute the numeral 3 for x wherever x appears in the equation. |
THE DIVISION RULE
OBJECTIVES
Upon completing this section you should be able to:
- Use the division rule to solve equations.
- Solve some basic applied problems whose solutions involve using the division rule.
As mentioned earlier, we wish to present an orderly procedure for solving equations. This procedure will involve the four basic operations, the first of which is presented in this section.
If each term of an equation is divided by the same nonzero number, the resulting equation is equivalent to the original equation.
To prepare to use the division rule for solving equations we must make note of the following process:

(We usually write 1x as x with the coefficient 1 understood.)
Example 1 Solve for x: 3x = 10
Solution
Our goal is to obtain x = some number. The division rule allows us to divide each term of 3x = 10 by the same number, and our goal of finding a value of x would indicate that we divide by 3. This would give us a coefficient of 1 for x.
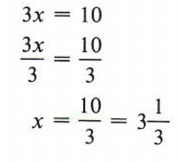
Check: 3x = 10 and x = ![]() these equivalent equations?
these equivalent equations?
We substitute ![]() for x in the first equation obtaining
for x in the first equation obtaining
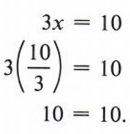
The equations are equivalent, so the solution is correct.
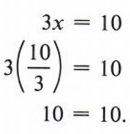
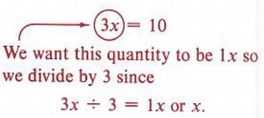
| Always Check! |
Example 2 Solve for x: 5x = 20
Solution
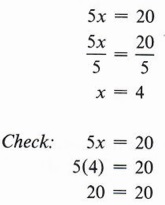
| Notice that the division rule does not allow us to divide by zero. Since dividing by zero is not allowed in mathematics, expressions such as |
Example 3 Solve for x: 8x = 4
Solution

| Errors are sometimes made in very simple situations. Don't glance at this problem and arrive at x = 2! Note that the division rule allows us to divide each term of an equation by any nonzero number and the resulting equation is equivalent to the original equation. Therefore we could divide each side of the equation by 5 and obtain Dividing by 5 does not help find the solution however. What number should we divide by to find the solution? |
Example 4 Solve for x: 0.5x = 6
Solution
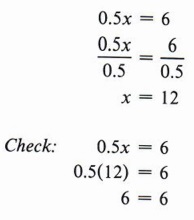

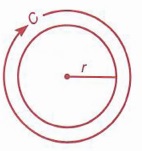
Example 6 The formula for finding the circumference (C) of a circle is C = 2πr, where π represents the radius of the circle and it is approximately 3.14. Find the radius of a circle if the circumference is measured to be 40.72 cm. Give the answer correct to two decimal places.
Solution
To solve a problem involving a formula we first use the substitution principle.

| Circumference means "distance around." It is the perimeter of a circle. The radius is the distance from the center to the circle. |
THE SUBTRACTION RULE
OBJECTIVES
Upon completing this section you should be able to use the subtraction rule to solve equations.
The second step toward an orderly procedure for solving equations will be discussed in this section. You will use your knowledge of like terms from chapter l as well as the techniques from section THE DIVISION RULE. Notice how new ideas in algebra build on previous knowledge.
If the same quantity is subtracted from both sides of an equation, the resulting equation will be equivalent to the original equation.
Example 1 Solve for x if x + 7 = 12.
Solution
Even though this equation can easily be solved mentally, we wish to illustrate the subtraction rule. We should think in this manner:
"I wish to solve for x so I need x by itself on one side of the equation. But I have x + 7. So if I subtract 7 from x + 7, I will have x alone on the left side." (Remember that a quantity subtracted from itself gives zero.) But if we subtract 7 from one side of the equation, the rule requires us to subtract 7 from the other side as well. So we proceed as follows:
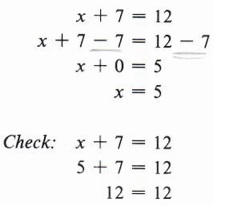
| Note that x + 0 may be written simply as x since zero added to any quantity equals the quantity itself. |
Example 2 Solve for x: 5x = 4x + 3
Solution
Here our thinking should proceed in this manner. "I wish to obtain all unknown quantities on one side of the equation and all numbers of arithmetic on the other so I have an equation of the form x = some number. I thus need to subtract Ax from both sides."
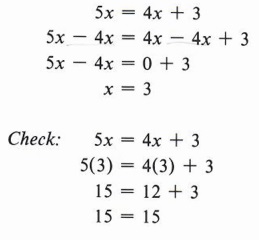
| Our goal is to arrive at x = some number. Remember that checking your solution is an important step in solving equations. |
Example 3 Solve for x: 3x + 6 = 2x + 11
Here we have a more involved task. First subtract 6 from both sides.
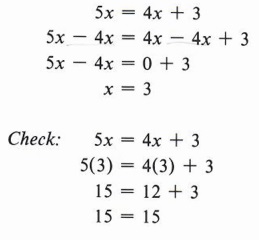
Now we must eliminate 2x on the right side by subtracting 2x from both sides.
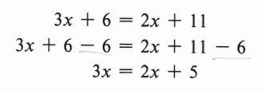
We now look at a solution that requires the use of both the subtraction rule and the division rule.
| Note that instead of first subtracting 6 we could just as well first subtract 2x from both sides obtaining 3x - 2x + 6 = 2x - 2x + 11 x + 6 = 11. Then subtracting 6 from both sides we have x + 6 - 6 = 11 - 6 x = 5. Keep in mind that our goal is x = some number. |
Example 4 Solve for x: 3x + 2 = 17
Solution
We first use the subtraction rule to subtract 2 from both sides obtaining
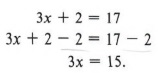
Then we use the division rule to obtain
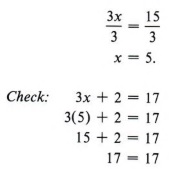
| Always check! |
Example 5 Solve for x: 7x + 1 = 5x + 9
Solution
We first use the subtraction rule.
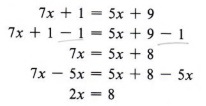
Then the division rule gives us
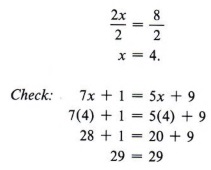
Example 6 The perimeter (P) of a rectangle is found by using the formula P = 2l+ 2w, where l stands for the length and w stands for the width. If the perimeter of a rectangle is 54 cm and the length is 15 cm, what is the width?
Solution
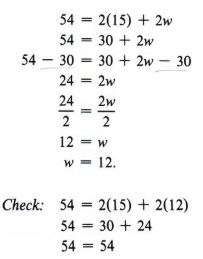
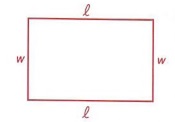
| Perimeter is the distance around. Do you see why the formula is P = 2l + 2w? |
THE ADDITION RULE
OBJECTIVES
Upon completing this section you should be able to use the addition rule to solve equations.
We now proceed to the next operation in our goal of developing an orderly procedure for solving equations. Once again, we will rely on previous knowledge.
If the same quantity is added to both sides of an equation, the resulting equation will be equivalent to the original equation.
Example 1 Solve for x if x - 7 = 2.
Solution
As always, in solving an equation we wish to arrive at the form of "x = some number." We observe that 7 has been subtracted from x, so to obtain x alone on the left side of the equation, we add 7 to both sides.
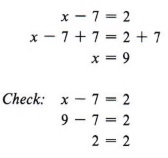
| Remember to always check your solution. |
Example 2 Solve for x: 2x - 3 = 6
Solution
Keeping in mind our goal of obtaining x alone, we observe that since 3 has been subtracted from 2x, we add 3 to both sides of the equation.
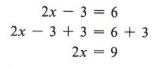
Now we must use the division rule.
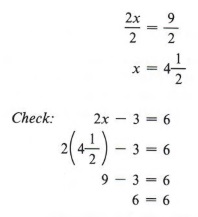
| Why do we add 3 to both sides? Note that in the example just using the addition rule does not solve the problem. |
Example 3 Solve for x: 3x - 4 = 11
Solution
We first use the addition rule.
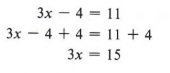
Then using the division rule, we obtain

| Here again, we needed to use both the addition rule and the division rule to solve the equation. |
Example 4 Solve for x: 5x = 14 - 2x
Solution
Here our goal of obtaining x alone on one side would suggest we eliminate the 2x on the right, so we add 2x to both sides of the equation.
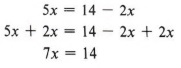
We next apply the division rule.
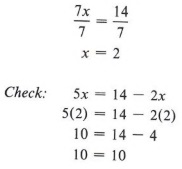
| Here again, we needed to use both the addition rule and the division rule to solve the equation. Note that we check by always substituting the solution in the original equation. |
Example 5 Solve for x: 3x - 2 = 8 - 2x
Solution
Here our task is more involved. We must think of eliminating the number 2 from the left side of the equation and also the lx from the right side to obtain x alone on one side. We may do either of these first. If we choose to first add 2x to both sides, we obtain
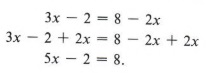
We now add 2 to both sides.
![]()
Finally the division rule gives
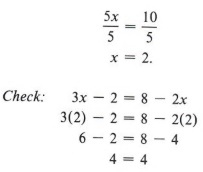
| Could we first add 2 to both sides? Try it! |
THE MULTIPLICATION RULE
OBJECTIVES
Upon completing this section you should be able to:
- Use the multiplication rule to solve equations.
- Solve proportions.
- Solve some basic applied problems using the multiplication rule.
We now come to the last of the four basic operations in developing our procedure for solving equations. We will also introduce ratio and proportion and use the multiplication rule to solve proportions.
If each term of an equation is multiplied by the same nonzero number, the resulting equation is equivalent to the original equation.
In elementary arithmetic some of the most difficult operations are those involving fractions. The multiplication rule allows us to avoid these operations when solving an equation involving fractions by finding an equivalent equation that contains only whole numbers.
Remember that when we multiply a whole number by a fraction, we use the rule ![]()
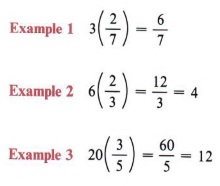
We are now ready to solve an equation involving fractions.
| Note that in each case only the numerator of the fraction is multiplied by the whole number. |
Example 4 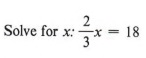
Solution
Keep in mind that we wish to obtain x alone on one side of the equation. We also would like to obtain an equation in whole numbers that is equivalent to the given equation. To eliminate the fraction in the equation we need to multiply by a number that is divisible by the denominator 3. We thus use the multiplication rule and multiply each term of the equation by 3.
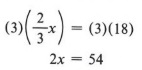
We now have an equivalent equation that contains only whole numbers. Using the division rule, we obtain
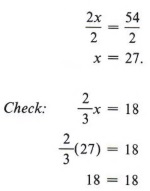
| To eliminate the fraction we need to multiply by a number that is divisible by the denominator. In the example we need to multiply by a number that is divided by 3. We could have multiplied both sides by 6, 9, 12, and so on, but the equation is simpler and easier to work with if wc use the smallest multiple. |
Example 5 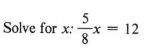
Solution

| See if you obtain the same solution by multiplying each side of the original equation by 16. Always check in the original equation. |
Example 6 ![]()
Solution
Here our task is the same but a little more complex. We have two fractions to eliminate. We must multiply each term of the equation by a number that is divisible by both 3 and 5. It is best to use the least of such numbers, which you will recall is the least common multiple. We will therefore multiply by 15.
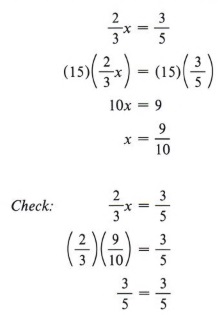
| In arithmetic you may have referred to the least common multiple as the "lowest common denominator." |
Example 7 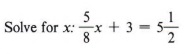
Solution
The least common multiple for 8 and 2 is 8, so we multiply each term of the equation by 8.
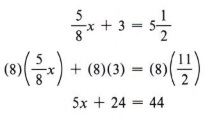
We now use the subtraction rule.
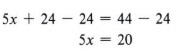
Finally the division rule gives us

| Before multiplying, change any mixed numbers to improper fractions. In this example change Remember that each term must be multiplied by 8. Note that in this example we used three rules to find the solution. |
Solving simple equations by multiplying both sides by the same number occurs frequently in the study of ratio and proportion.
A ratio is the quotient of two numbers.
The ratio of a number x to a number y can be written as x:y or ![]() . In general, the fractional form is more meaningful and useful. Thus, we will write the ratio of 3 to 4 as
. In general, the fractional form is more meaningful and useful. Thus, we will write the ratio of 3 to 4 as ![]() .
.
A proportion is a statement that two ratios are equal.
Example 8 ![]()
Solution
We need to find a value of x such that the ratio of x to 15 is equal to the ratio of 2 to 5.
Multiplying each side of the equation by 15, we obtain
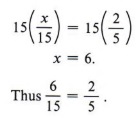
| Why do we multiply both sides by 15? Check this solution in the original equation. |
Example 9 What number x has the same ratio to 3 as 6 has to 9?
Solution
To solve for x we first write the proportion: ![]()
Next we multipy each side of the equation by 9.


| Say to yourself, "2 is to 5 as x is to 10." Check! |
Example 11 The ratio of the number of women to the number of men in a math class is 7 to 8. If there are 24 men in the class, how many women are in the class?
Solution

| Check! |
Example 12 Two sons were to divide an inheritance in the ratio of 3 to 5. If the son who received the larger portion got $20,000, what was the total amount of the inheritance?
Solution
We now add $20,000 + $12,000 to obtain the total amount of $32,000.
| Check! Again, be careful in setting up the proportion. In the ratio 3/5, 5 is the larger portion. Therefore, since $20,000 is the larger portion, it must also appear in the denominator. |
Example 13 If the legal requirements for room capacity require 3 cubic meters of air space per person, how many people can legally occupy a room that measures 6 meters wide, 8 meters long, and 3 meters high?
Solution

So, 48 people would be the legal room capacity.
| This means "1 person is to 3 cubic meters as x people are to 144 cubic meters." Check the solution. |
COMBINING RULES FOR SOLVING EQUATIONS
OBJECTIVES
Upon completing this section you should be able to:
- Use combinations of the various rules to solve more complex equations.
- Apply the orderly steps established in this section to systematically solve equations.
Many of the exercises in previous sections have required the use of more than one rule in the solution process. In fact, it is possible that a single problem could involve all the rules
There is no mandatory process for solving equations involving more than one rule, but experience has shown that the following order gives a smoother, more mistake-free procedure.
First Eliminate fractions, if any, by multiplying each term of the equation by the least common multiple of all denominators of fractions in the equation.
Second Simplify by combining like terms on each side of the equation.
Third Add or subtract the necessary quantities to obtain the unknown quantity on one side and the numbers of arithmetic on the other side.
Fourth Divide by the coefficient of the unknown quantity.
Fifth Check your answer.
| Remember, the coefficient is the number being multiplied by the letter. (That is, in the expression 5x the coefficient is 5.) |

| Again, make sure every term is multiplied by 3. |
Solution
Multiplying each term by 15 yields
You may want to leave your answer as an improper fraction instead of a mixed number. Either form is correct, but the improper fraction form will be more useful in checking your solution.
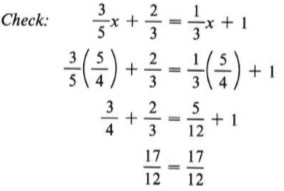
| Note that there are four terms in this equation. |
Example 3 The selling price (S) of a certain article was $30.00. If the margin (M) was one-fifth of the cost (C), find the cost of the article. Use the formula C + M = S.
Solution
Since the margin was one-fifth of the cost, we may write

![]()
SUMMARY
Key Words
- An equation is a statement in symbols that two number expressions are equal.
- An identity is true for all values of the literal and arithmetic numbers in it.
- A conditional equation is true for only certain values of the literal numbers in it.
- A solution or root of an equation is the value of the variable that makes the equation a true statement.
- Two equations are equivalent if they have the same solution set.
- A ratio is the quotient of two numbers.
- A proportion is a statement that two ratios are equal.
Procedures
- If each term of an equation is divided by the same nonzero number, the resulting equation is equivalent to the original equation.
- If the same quantity is subtracted from both sides of an equation, the resulting equation is equivalent to the original equation.
- If the same quantity is added to both sides of an equation, the resulting equation is equivalent to the original equation.
- If each side of an equation is multiplied by the same nonzero number, the resulting equation is equivalent to the original equation.
- To solve an equation follow these steps:
Step 1 Eliminate fractions by multiplying each term by the least common multiple of all denominators in the equation.
Step 2 Combine like terms on each side of the equation.
Step 3 Add or subtract terms to obtain the unknown quantity on one side and the numbers of arithmetic on the other.
Step 4 Divide each term by the coefficient of the unknown quantity.
Step 5 Check your answer.