Calculus
The calculus section of QuickMath allows you to differentiate and integrate almost any mathematical expression.
What is calculus?
Calculus is a vast topic, and it forms the basis for much of modern mathematics. The two branches of calculus are differential calculus and integral calculus.
Differential calculus is the study of rates of change of functions. At school, you are introduced to differential calculus by learning how to find the derivative of a function in order to determine the slope of the graph of that function at any point.
Integral calculus is often introduced in school in terms of finding primitive functions (indefinite integrals) and finding the area under a curve (definite integrals).
Differentiate
The differentiate command allows you to find the derivative of an expression with respect to any variable. In the advanced section, you also have the option of specifying arbitrary functional dependencies within your expression and finding higher order derivatives. The differentiate command knows all the rules of differential calculus, including the product rule, the quotient rule and the chain rule.
Integrate
The integrate command can be used to find either indefinite or definite integrals. If an indefinite integral (primitive function) is sought but cannot be found for a particular function, QuickMath will let you know. Definite integrals will always be given in their exact form when possible, but failing this QuickMath will use a numerical method to give you an approximate value.
The Fundamental Theorem of Calculus
Integrals were evaluated in the previous tutorial by identifying the integral with an appropriate area and then using methods from geometry to find the area. This procedure will succeed only for very simple integrals. The main result of this section, the fundamental theorem of calculus, includes a very important formula for evaluating integrals. This theorem shows us how to evaluate integrals by first evaluating antiderivatives. The theorem establishes an amazing relationship between the integral, which may be interpreted as an area, and the antiderivative, which is inversely related to the derivative; that is, it relates area and the derivative.
Theorem 1
Let f be a continuous function on [a, b ], and define a function F by
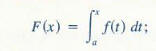
then
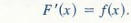
This result could also be written as
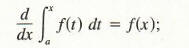
that is, the derivative of the integral of/ with respect to the upper limit of
integration x is equal to f evaluated at x. We shall verify a special case of
this theorem at the end of this section. Example I illustrates Theorem l.
Example 1
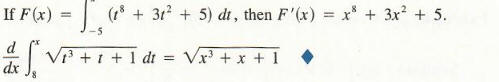
The following theorem is called the fundamental theorem and is a consequence
of Theorem 1 .
The Fundamental Theorem of Calculus
Let f be continuous on [a. b ], and suppose G is any antiderivative of f on
[a, b], that is. G'(x) = f(x) for x in [a. b]. Then,
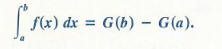
To verify the fundamental theorem, let F be given by
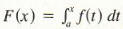, as in Formula (1). Then by Theorem 1, F is
an antiderivative of f. Since G is also an antiderivative of f, we know that
there is a constant c for which F(x} = G(x) + c.
Since F(a) = J;' f(x) dx = 0, it follows that
0 = F (a) = G (a) + c
and hence c = -G(a). Thus, F(x) = G(x) + c = G(x) - G(a), from which we see
that
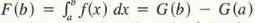
For convenience, we introduce the following notation:
With this notation, Formula (4) can be written as
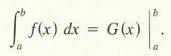
The following equivalent formula demonstrates the convenience of using a symbol
for the integral that resembles the one for the antiderivative.
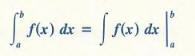
This formula is a consequence of the fact that integral of f(x) dx
is the most general anti derivative of f.