Equations and Inequalities Involving Signed Numbers
In chapter 2 we established rules for solving equations using the numbers of arithmetic. Now that we have learned the operations on signed numbers, we will use those same rules to solve equations that involve negative numbers. We will also study techniques for solving and graphing inequalities having one unknown.
SOLVING EQUATIONS INVOLVING SIGNED NUMBERS
OBJECTIVES
Upon completing this section you should be able to solve equations involving signed numbers.
Example 1 Solve for x and check: x + 5 = 3
Solution
Using the same procedures learned in chapter 2, we subtract 5 from each side of the equation obtaining
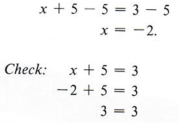
Example 2 Solve for x and check: - 3x = 12
Solution
Dividing each side by -3, we obtain
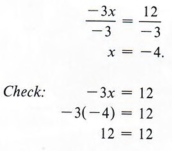
| Always check in the original equation. |
| Another way of solving the equation 3x - 4 = 7x + 8 would be to first subtract 3x from both sides obtaining -4 = 4x + 8, then subtract 8 from both sides and get -12 = 4x. Now divide both sides by 4 obtaining - 3 = x or x = - 3. |
| First remove parentheses. Then follow the procedure learned in chapter 2. |
LITERAL EQUATIONS
OBJECTIVES
Upon completing this section you should be able to:
- Identify a literal equation.
- Apply previously learned rules to solve literal equations.
An equation having more than one letter is sometimes called a literal equation. It is occasionally necessary to solve such an equation for one of the letters in terms of the others. The step-by-step procedure discussed and used in chapter 2 is still valid after any grouping symbols are removed.
Example 1 Solve for c: 3(x + c) - 4y = 2x - 5c
Solution
First remove parentheses.
At this point we note that since we are solving for c, we want to obtain c on one side and all other terms on the other side of the equation. Thus we obtain
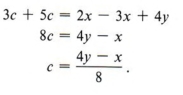
| Remember, abx is the same as 1abx. We divide by the coefficient of x, which in this case is ab. |
| Solve the equation 2x + 2y - 9x + 9a by first subtracting 2.v from both sides. Compare the solution with that obtained in the example. |
Sometimes the form of an answer can be changed. In this example we could multiply both numerator and denominator of the answer by (- l) (this does not change the value of the answer) and obtain
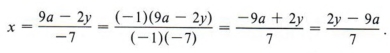
The advantage of this last expression over the first is that there are not so many negative signs in the answer.
| Multiplying numerator and denominator of a fraction by the same number is a use of the fundamental principle of fractions. |
The most commonly used literal expressions are formulas from geometry, physics, business, electronics, and so forth.
Example 4 
is the formula for the area of a trapezoid. Solve for c.
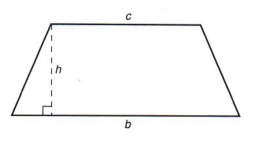
| A trapezoid has two parallel sides and two nonparallel sides. The parallel sides are called bases. Removing parentheses does not mean to merely erase them. We must multiply each term inside the parentheses by the factor preceding the parentheses. Changing the form of an answer is not necessary, but you should be able to recognize when you have a correct answer even though the form is not the same. |
Example 5 
is a formula giving interest (I) earned for a period of D days when the principal (p) and the yearly rate (r) are known. Find the yearly rate when the amount of interest, the principal, and the number of days are all known.
Solution
The problem requires solving for r.
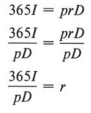
Notice in this example that r was left on the right side and thus the computation was simpler. We can rewrite the answer another way if we wish.
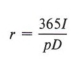
GRAPHING INEQUALITIES
OBJECTIVES
Upon completing this section you should be able to:
- Use the inequality symbol to represent the relative positions of two numbers on the number line.
- Graph inequalities on the number line.
We have already discussed the set of rational numbers as those that can be expressed as a ratio of two integers. There is also a set of numbers, called the irrational numbers,, that cannot be expressed as the ratio of integers. This set includes such numbers as 
and so on. The set composed of rational and irrational numbers is called the real numbers.
Given any two real numbers a and b, it is always possible to state that 
Many times we are only interested in whether or not two numbers are equal, but there are situations where we also wish to represent the relative size of numbers that are not equal.
The symbols < and > are inequality symbols or order relations and are used to show the relative sizes of the values of two numbers. We usually read the symbol < as "less than." For instance, a < b is read as "a is less than b." We usually read the symbol > as "greater than." For instance, a > b is read as "a is greater than b." Notice that we have stated that we usually read a < b as a is less than b. But this is only because we read from left to right. In other words, "a is less than b" is the same as saying "b is greater than a." Actually then, we have one symbol that is written two ways only for convenience of reading. One way to remember the meaning of the symbol is that the pointed end is toward the lesser of the two numbers.
| The statement 2 < 5 can be read as "two is less than five" or "five is greater than two." |
a < b, "a is less than bif and only if there is a positive number c that can be added to a to give a + c = b.
| What positive number can be added to 2 to give 5? |
In simpler words this definition states that a is less than b if we must add something to a to get b. Of course, the "something" must be positive.
If you think of the number line, you know that adding a positive number is equivalent to moving to the right on the number line. This gives rise to the following alternative definition, which may be easier to visualize.
Example 1 3 < 6, because 3 is to the left of 6 on the number line.
| We could also write 6 > 3. |
Example 2 - 4 < 0, because -4 is to the left of 0 on the number line.
| We could also write 0 > - 4. |
Example 3 4 > - 2, because 4 is to the right of -2 on the number line.
Example 4 - 6 < - 2, because -6 is to the left of -2 on the number line.
The mathematical statement x < 3, read as "x is less than 3," indicates that the variable x can be any number less than (or to the left of) 3. Remember, we are considering the real numbers and not just integers, so do not think of the values of x for x < 3 as only 2, 1,0, - 1, and so on.
| Do you see why finding the largest number less than 3 is impossible? |
As a matter of fact, to name the number x that is the largest number less than 3 is an impossible task. It can be indicated on the number line, however. To do this we need a symbol to represent the meaning of a statement such as x < 3.
The symbols ( and ) used on the number line indicate that the endpoint is not included in the set.
Example 5 Graph x < 3 on the number line.
Solution
Note that the graph has an arrow indicating that the line continues without end to the left.
| This graph represents every real number less than 3. |
Example 6 Graph x > 4 on the number line.
Solution
| This graph represents every real number greater than 4. |
Example 7 Graph x > -5 on the number line.
Solution
| This graph represents every real number greater than -5. |
Example 8 Make a number line graph showing that x > - 1 and x < 5. (The word "and" means that both conditions must apply.)
Solution
The statement x > - 1 and x < 5 can be condensed to read - 1 < x < 5.
| This graph represents all real numbers that are between - 1 and 5. |
Example 9 Graph - 3 < x < 3.
Solution
If we wish to include the endpoint in the set, we use a different symbol, 
:. We read these symbols as "equal to or less than" and "equal to or greater than."
Example 10 x >; 4 indicates the number 4 and all real numbers to the right of 4 on the number line.
| What does x < 4 represent? |
The symbols [ and ] used on the number line indicate that the endpoint is included in the set.
| You will find this use of parentheses and brackets to be consistent with their use in future courses in mathematics. |
| This graph represents the number 1 and all real numbers greater than 1. |
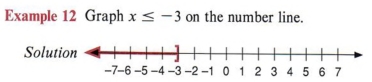
| This graph represents the number 1 and all real numbers less than or equal to - 3. |
Example 13 Write an algebraic statement represented by the following graph.
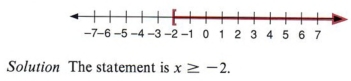
Example 14 Write an algebraic statement for the following graph.
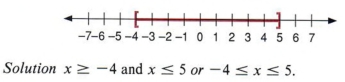
| This graph represents all real numbers between -4 and 5 including -4 and 5. |
Example 15 Write an algebraic statement for the following graph.
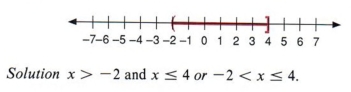
| This graph includes 4 but not -2. |
Example 16 Graph 
on the number line.
Solution
This example presents a small problem. How can we indicate on the number line? If we estimate the point, then another person might misread the statement. Could you possibly tell if the point represents or maybe 
? Since the purpose of a graph is to clarify, always label the endpoint.
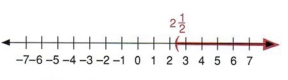
| A graph is used to communicate a statement. You should always name the zero point to show direction and also the endpoint or points to be exact. |
SOLVING INEQUALITIES
OBJECTIVES
Upon completing this section you should be able to solve inequalities involving one unknown.
The solutions for inequalities generally involve the same basic rules as equations. There is one exception, which we will soon discover. The first rule, however, is similar to that used in solving equations.
If the same quantity is added to each side of an inequality, the results are unequal in the same order.
Example 1 If 5 < 8, then 5 + 2 < 8 + 2.
Example 2 If 7 < 10, then 7 - 3 < 10 - 3.
| 5 + 2 < 8 + 2 becomes 7 < 10. 7 - 3 < 10 - 3 becomes 4 < 7. |
We can use this rule to solve certain inequalities.
Example 3 Solve for x: x + 6 < 10
Solution
If we add -6 to each side, we obtain
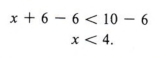
Graphing this solution on the number line, we have
| Note that the procedure is the same as in solving equations. |
We will now use the addition rule to illustrate an important concept concerning multiplication or division of inequalities.
Suppose x > a.
Now add - x to both sides by the addition rule.
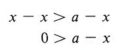
| Remember, adding the same quantity to both sides of an inequality does not change its direction. |
Now add -a to both sides.
The last statement, - a > -x, can be rewritten as - x < -a. Therefore we can say, "If x > a, then - x < -a. This translates into the following rule:
If an inequality is multiplied or divided by a negative number, the results will be unequal in the opposite order.
| For example: If 5 > 3 then -5 < -3. |
Example 5 Solve for x and graph the solution: -2x>6
Solution
To obtain x on the left side we must divide each term by - 2. Notice that since we are dividing by a negative number, we must change the direction of the inequality.
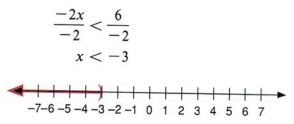
| Notice that as soon as we divide by a negative quantity, we must change the direction of the inequality. |
Take special note of this fact. Each time you divide or multiply by a negative number, you must change the direction of the inequality symbol. This is the only difference between solving equations and solving inequalities.
| When we multiply or divide by a positive number, there is no change. When we multiply or divide by a negative number, the direction of the inequality changes. Be careful-this is the source of many errors. |
Once we have removed parentheses and have only individual terms in an expression, the procedure for finding a solution is almost like that in chapter 2.
Let us now review the step-by-step method from chapter 2 and note the difference when solving inequalities.
First Eliminate fractions by multiplying all terms by the least common denominator of all fractions. (No change when we are multiplying by a positive number.)
Second Simplify by combining like terms on each side of the inequality. (No change)
Third Add or subtract quantities to obtain the unknown on one side and the numbers on the other. (No change)
Fourth Divide each term of the inequality by the coefficient of the unknown. If the coefficient is positive, the inequality will remain the same. If the coefficient is negative, the inequality will be reversed. (This is the important difference between equations and inequalities.)
| The only possible difference is in the final step. |
| What must be done when dividing by a negative number? |
| Don’t forget to label the endpoint. |
SUMMARY
Key Words
- A literal equation is an equation involving more than one letter.
- The symbols < and > are inequality symbols or order relations.
- a < b means that a is to the left of b on the real number line.
- The double symbols
![]()
: indicate that the endpoints are included in the solution set.
Procedures
- To solve a literal equation for one letter in terms of the others follow the same steps as in chapter 2.
- To solve an inequality use the following steps:
Step 1 Eliminate fractions by multiplying all terms by the least common denominator of all fractions.
Step 2 Simplify by combining like terms on each side of the inequality.
Step 3 Add or subtract quantities to obtain the unknown on one side and the numbers on the other.
Step 4 Divide each term of the inequality by the coefficient of the unknown. If the coefficient is positive, the inequality will remain the same. If the coefficient is negative, the inequality will be reversed.
Step 5 Check your answer.