Language of Algebra

Using letters to represent numbers is a fundamental characteristic of algebra.
In this chapter, letters will represent the numbers of arithmetic. As you become familiar with the symbols and terminology of algebra, operations on arithmetic numbers will be reviewed.
 

SOME SYMBOLS FOR OPERATIONS
 

OBJECTIVES

Upon completing this section you should be able to:
1. Identify the operation symbols of arithmetic.
2. Perform these operations on whole numbers, fractions, and decimals.

Remember that when adding or subtracting fractions, you must find a common denominator.

When adding or subtracting decimals, align the decimal points.

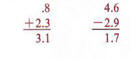
In multiplying fractions multiply numerators to obtain the numerator of the product and multiply denominators to obtain the denominator of the product.

The symbol + is used to indicate a sum. a + b (read as "a plus b") is used to indicate the sum of a and b.

 

The symbol - is used to indicate the operation of subtraction, a - b (read as "a minus b") indicates the difference of the numbers a and b.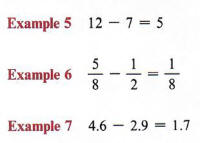

The operation of multiplication (the product of two numbers) can be represented in several ways. You should become familiar with each of these.
 

1. The symbol X is often used to represent multiplication, a X b (read as "a times b") represents the product of the two numbers a and b.

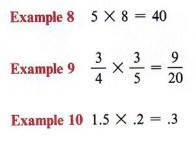
The symbol X is not usually used with letters in algebra because it can be confused with the letter X.

2. a * b (read as "a times b") is also used to represent the product of the numbers a and b.
The symbol * is not usually used with numbers because it could be confused with a decimal point.
 

3. If two letters or a number and a letter are written together without an operation sign, multiplication is indicated.

 

The process of writing two letters or a number and a letter together without an operation sign is called juxtaposition. This method of indicating multiplication cannot be used for two numbers, since 52 does not mean "5 times 2."

4. When two sets of parentheses have no operation sign between them, multiplication is indicated, (a)(6) means "a times b." Also, a letter or number preceding a parenthesis with no sign in between indicates multiplication. a{b) means "a times 6" and 7(x) means "7 times x."

4.2 * 5.1 would be a confusing way to indicate the product of 4.2 and 5.1.
Notice that the sum or product of two numbers does not change if we reverse the order in which they are written. For example,
3 + 5 = 8; also 5 + 3 = 8
4 * 6 = 24 and 6 * 4 = 24. This characteristic is called the commutative property.
Does this property hold for subtraction?
(Consider 7 - 2 and 2 - 7.)

(4.2)(5.1) is a much better way to indicate the product of these two numbers than the ways shown earlier.
Recall that division is the inverse operation of multiplication. Therefore,

 

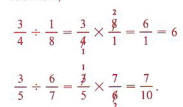
Complete the following:

Is division commutative?

This information will be helpful to remember as you work the problems in the following exercise set.
Remember to reduce fractions.

Of these several methods for indicating a product, the last two are most commonly used.
The quotient of two numbers, a and b, can be written in two ways,and - both indicate "the number a is divided by the number b."

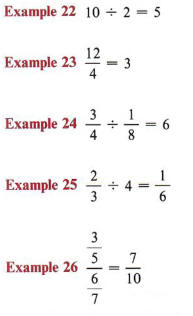
The fractional representation for division is most commonly used in algebra.

Recall from arithmetic that a fraction whose numerator is greater than the denominator is called an improper fraction.
Therefore,

 

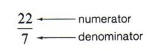
is an improper fraction.
Recall also that an improper fraction can be written as a mixed number.

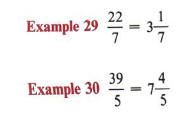
Likewise, a mixed number may be written as an improper fraction.

Improper fraction form is generally a more convenient form to work with. If division or multiplication is to be performed, then improper fraction form is almost a necessity.

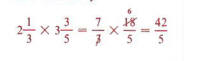
Some problems may involve only one operation, while others may require two or more.

It is important to know the symbols for the various operations. It is also important to know what operation or series of operations to use in solving a specific  We meet these problems every day.

Solution The operation is addition. We would indicate the total cost as
$1.89 + $.65 + $.59.
Then adding, we obtain
$1.89 + $.65 + $.59 = $3.13.
 

The operation of subtraction often occurs in problems that involve making change, balancing checkbooks, and discounting prices. In preparation for later work get used to using parentheses to indicate multiplication.

Solution The operation in this example is subtraction. We need to subtract the cost of the order from $5.00.
$5.00 - $3.13 = $1.87

Solution This is a multiplication problem. We multiply the hourly wage by the number of hours worked.
5 X $4.50
0r 5($4.50) = $22.50
 

Solution This is a division problem. We must divide the cost of the boat by the number of people.
 

$4,200 -5- 3 = $1,400
 

Often problems involve more than one arithmetic operation.
 

We could also write this as

 

Solution This problem involves both multiplication and subtraction. We first need to find 20% of $529. To do this we multiply $529 by the decimal equivalent of 20%.
.20($529) = $105.80

Remember, to change a percent to a decimal move the decimal point two places to the left

This is the amount of the discount. To find the sale price we now , must subtract $105.80 from the regular price.
$529.00 - $105.80 = $423.20

GROUPING SYMBOLS
 

OBJECTIVES
Upon completing this section you should be able to:
1. Perform operations in the correct order indicated by grouping symbols.
2. Perform operations in a specific order when grouping symbols are not used.
 

Parentheses ( ), brackets [ ], and braces j } are all used as grouping symbols in algebra. A number expression enclosed in a grouping symbol is treated as if it were a single number.

Example 1 12 - (3 + 4) indicates that the sum (3 + 4) is subtracted from 12. 12 - (3 + 4) = 12 - 7 = 5. Note that without parentheses, 12 - 3 + 4 = 13.

Example 2 7(5 + x) indicates that the sum (5 + x) is multiplied by 7.
In general, operations within the grouping symbols are performed first. Brackets and braces can be used instead of parentheses.
12 - [3 + 4] and 12 - {3 + 4} mean the same as 12 - (3 + 4).
Some applications may require the use of grouping symbols.
 

Example 3 A bank account has a balance of $567.19. Checks are written for $18.50, $24.95, and $129.40. What is the new balance?

Parentheses are most commonly used when no other grouping symbols are involved.
 

Solution We need to add the amounts of the three checks and subtract the sum from the original balance. We therefore write
$567.19 - ($18.50 + $24.95 + $129.40) = $567.19 - $172.85 = $394.34.

The first step is to simplify what is inside the parentheses.

As mentioned earlier, an expression may have a different value if parentheses are not used. We saw that
12 - (3 + 4) = 5,
 

but it was stated that without parentheses
12 - 3 + 4 = 13.
 

This is due to the following rule:

If an expression without grouping symbols contains only additions and subtractions, these operations are performed in order from left to right.

 

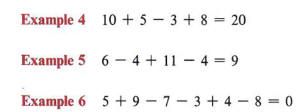
If an expression contains operations other than just addition and subtraction, we use the following rule:
 

If no grouping symbols occur in an expression, multiplication and division are performed from left to right and then addition and subtraction from left to right.
 

Notice that when adding three numbers, the order in which they are added does not affect the sum.
3 + (8 + 4) = 3 + 12 = 15 (3 + 8) + 4 = 11 + 4 = 15 This characteristic is called the associative property. Is multiplication associative?

Sometimes more than one set of grouping symbols is needed in an expression. When this occurs we use brackets or braces along with parentheses for clarification. For instance, 5 + [7 - (2 + 1)] could be written using only parentheses, but 5 + (7 - (2 + 1)) is not as clear at first glance. Therefore, we alternate the symbols to avoid confusion. To evaluate such an expression, we use the following rule:

When simplifying an expression containing grouping symbols within grouping symbols, remove the innermost set of symbols first.

In using this rule do not try to do more than one operation at a time.

Example 10 To evaluate 5 + [7 - (2 + 1)] we simplify the innermost set of symbols, namely (2 + 1). Writing (2 + 1) as 3, we now obtain

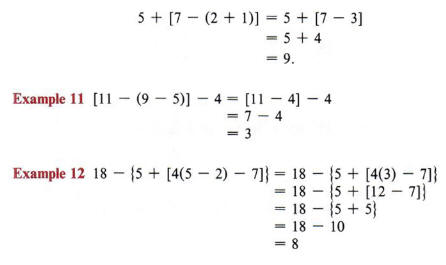
Remember that the different symbols are all used for the same purpose-to group numbers.
Again, make sure you do only one operation at a time. This is very important in order to avoid errors.
Notice that we start with (5 - 2) since it is the innermost set of symbols.

 

ALGEBRAIC EXPRESSIONS
 

When letters are used to represent numbers, they are called literal numbers. If a number expression contains one or more literal numbers, it is called a literal expression or algebraic expression.
 

OBJECTIVES
Upon completing this section you should be able to:
1. Write literal expressions involving operations of arithmetic.
2. Identify terms and factors of an expression.

Example 1 x + 5 represents "the sum of x and 5." a - b represents "the difference of a and b." 4y represents "the product of 4 and y."
When we refer to the difference of two numbers, the second number is always subtracted from the first.
 

Example 2 Write a literal expression for "the sum of x and 5, divided by 7."
Solution
(x + 5) represents "the sum of x and 5," so we have (x + 5) / 7. Notice that parentheses are necessary if we write the above as (x + 5) / 7.
Notice that the comma is very important in example 2. Without the comma the statement would read as "the sum of x and 5 divided by 7." The literal expression would be

Example 3 Write an algebraic expression for "the difference of a and b, multiplied by the sum of a and b."
x + (5 -4- 7) or .V + -y .
Solution The difference of a and b is (o - b)\ the sum of a and b is (a + b), so we have (a - b)(a + b).

Notice again the importance of the use of the comma in example 3.

Example 4 Express c - (a + b) in words.
Solution Since (a + b) is in parentheses, it is "the sum of a and b." So we write c - (a + b) as "the difference of c, and the sum of a and b"

When an algebraic expression is composed of parts connected by addition or subtraction signs, these parts are called the terms of the expression.
 

Example 5 a + b has two terms.

In a + b the terms are a and b.

Example 6 2x + 5y + 3 has three terms: 2x, 5y and 3.
 

When an algebraic expression is composed of parts to be multiplied, these parts are called the factors of the expression.

Example 7 ab has two factors, a and b.

It is very important to be able to distinguish between terms and factors. Rules  that apply to terms will not, in general, apply to factors. When naming terms  or factors, it is necessary to regard the entire expression.

From now on through all of algebra you will be using the words term and factor. Make sure you understand the definitions.

Example 8 The expression 3x + 2y + 7 has three terms. Note that a term may contain factors (for example, the first term of this expression, 3x, contains two factors)-but the entire expression is made up of terms.

It should be noted that there are more than just four factors in the expression 5xyz. The obvious factors are 5, x, y, and z. But 5x is also a factor. Other factors are 5xy, xy, 5yz, xz, 5z, and so on.

An exponent is sometimes referred to as a "power." For example, 5³ could be referred to as "five to the third power."
Unless parentheses are used, the exponent only affects the factor directly preceding it.

Example 9 5xyz is one term made up of factors.

Example 10 3(a + b) is one term having two factors. Note here that the factor (a + b) has two terms, but the entire expression is made up of factors.
An exponent is a numeral used to indicate how many times a factor is to be used in a product.
An exponent is usually written as a smaller (in size) numeral slightly above and to the right of the factor affected by the exponent.

Stopped here

Note the difference between 2x³ and (2x)³. From the use of parentheses as grouping symbols we see that
2x³ means 2(x)(x)(x), whereas (2x)³ means (2x)(2x)(2x) or 8x³.
 

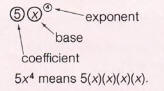
In an expression such as 5x⁴

1. 5 is the numerical coefficient or coefficient,
2. x is the base,
3. 4 is the exponent.
    

Many students make the error of multiplying the base by the exponent.
For example, they will say
3⁴ = 12 instead of the correct answer
3⁴= (3)(3)(3)(3) = 81.

Note that only the base is affected by the exponent.

Example 13 In the expression ax³
 

1. a is the coefficient,
2. x is the base,
3. 3 is the exponent.

ax³ means (a)(x)(x)(x).

Example 14 (ax)³
 

Solution 1 is the coefficient (understood), ax is the base (because of the parentheses), 3 is the exponent.
(ax)³ means (ax)(ax)(ax).

When we write a literal number such as x, it will be understood that the coefficient is one and the exponent is one. This can be very important in many operations.
 

x means 1x¹.

If an expression has grouping symbols, the operations therein are performed first.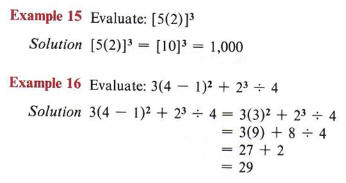

The coefficient, 1, is understood and usually we do not bother to write it in the expression.
Recall the order of operations.
 

EVALUATING LITERAL EXPRESSIONS

OBJECTIVES
Upon completing this section you should be able to:
1. Substitute numbers for letters in literal expressions.
2. Evaluate the expression once the substitutions have been made.
 

The principle of substitution states that any quantity may be substituted for its equal in any process. This principle is used extensively in algebra and we will use it here to evaluate literal expressions. In this process we substitute numbers for letters and find a numerical value.

Example 1 Evaluate x + 3 if x = 5.
We substitute 5 for x in the expression obtaining
5 + 3 = 8.
 

Example2 Evaluate 4a - 1 if a = 3.
We substitute 3 for a in the expression obtaining
4(3) -1 = 12-1
= 11.

Remember that in a literal expression the letters are merely holding a place for various numbers that may be assigned to them. For that reason, these letters are sometimes called place holders or variables.
 

To find the perimeter of a rectangle we need to add up all four sides, but since the opposite sides are equal, we only need to double the length and double the width, and then find their sum.
The height of a triangle is called the altitude of the triangle. It is the perpendicular distance from the base to the opposite corner, which is called the vertex.

One of the most common uses of evaluating literal expressions is in working with formulas.

Example 7 The perimeter (distance around) of a rectangle is found by using the formula P = 2l + 2w, where l represents the length and w represents the width.
 

 

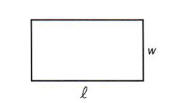
If the length of a rectangle is 10 and the width is 6, we may find the perimeter by substituting 10 for l and 6 for w.
 

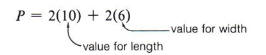P = 2(10) + 2(6)
P = 2(10) + 2(6) = 20+12 = 32.
 

Example 8 The area of a triangle is found by using the formula

 

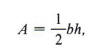
where b represents the base of the triangle and h represents the height.

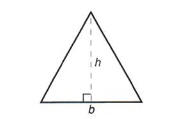
If we want to find the area of a triangle where the base is 10 and the height is 8, we would let b = 10 and h = 8. Substituting these values in the formula, we obtain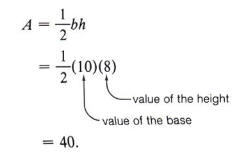

 

COMBINING LIKE TERMS
 

OBJECTIVES
Upon completing this section, you should be able to:
1. Identity like terms.
2. Combine like terms.
 

In the preceding sections we have presented symbols used in algebraic expressions. We now proceed to the operations of addition and subtraction on certain of these expressions.

Like terms are terms that have exactly the same literal factors.

Example 1 5x and 3x are like terms since they have the same literal factors, (x is the literal factor in each term.)

Example 2 5x and 3y are not like terms since the literal factors are not the same, (x and y are the literal factors.)

Example 3 3x²y and x²y are like terms since they have the same literal
factors (x² and y).

Example 4 3x²y² and 2xy are not like terms. They have different literal factors. (Note that x² and x are not the same.)

Only like terms can be combined. When two terms are like terms, combine the numerical coefficients to obtain the coefficient of the like common factors.

Example 5 If we add the like terms 5x + 3x, we combine the coefficients 5 and 3 obtaining
5x + 3x = (5 + 3)x = 8x.

 

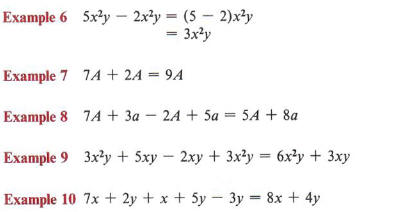
Many students make the mistake of interchanging capital and lowercase letters in an expression. In algebra a capital "A" and a lowercase "a" are considered just as different as x and y. Therefore, terms such as 5A and 3a would not be considered like terms. Be careful. Be consistent with the letters you use.

Notice that the numerical coefficient of x is 1 and in this example must be added to the 7 of lx.
 

Example 11 12 ab + 4 ba - 6 ab = 10 ab
By the commutative law of multiplication 4ba = 4ab.

Key Words

• Parentheses ( ), brackets [ ], and braces{ } are all used as grouping symbols in algebra.
• Literal numbers are letters used to represent numbers.
• An algebraic expression or literal expression is a number expression containing one or more literal numbers.
• Terms are those parts of an algebraic expression that are being added or subtracted.
  Factors are those parts of an algebraic expression that are being multiplied.
• An exponent indicates the number of times a factor is to be used in a product.
• The principle of substitution states that any quantity may be substituted for its equal in any process.
• Like terms are terms that have exactly the same literal factors.
   

Procedures

• If no grouping symbols occur in an expression, multiplication and division are performed from left to right, and then addition and subtraction from left to right.
• When simplifying an expression containing grouping symbols within grouping symbols, remove the innermost set of symbols first.
• To evaluate a literal expression substitute the given values for the literal numbers and perform the indicated operations.
• To combine like terms combine the numerical coefficients and use this result as the coefficient of the common literal factors.