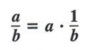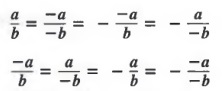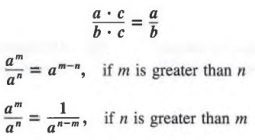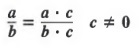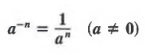INTEGER EXPONENTS AND SCIENTIFIC NOTATION

In this section, we will introduce another symbol for a fraction of the form and then we will use this symbol to write certain numbers in simpler form.

INTEGER EXPONENTS

Recall that we have defined a power aⁿ (where n is a natural number) as follows:

aⁿ = a · a · a · · · · · a (n factors)

We will now give meaning to powers in which the exponent is 0 or a negative integer. First, let us consider the quotient a⁴/a⁴. Using the property of quotients of powers, we have

Note that for any a not equal to zero, the left-hand member equals 1 and the right-hand member equals a⁰. In general, we define:

a⁰ = 1

for any number a except 0.

Example 1 a. 3⁰ = 1
b. 425⁰ = 1
c. (x²y)⁰ = 1

Now consider the quotient a⁴/a⁷. Using the two quotient laws for powers, we have

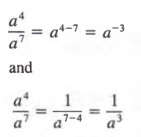
Thus, for any a not equal to 0, we can view a^-3 as equivalent to . In general, we define

for any number a except zero.

Example 2

SCIENTIFIC NOTATION

Very large numbers such as

5,980,000,000,000, 000,000,000,000,000

and very small numbers such as

0.000 000 000 000 000 000 000 001 67

occur in many scientific areas. Large numbers can be rewritten in a more compact and useful form by using powers with positive exponents. We can also rewrite small numbers by using powers with negative exponents that have been introduced in this section.

First, let us consider some factored forms of 38,400 in which one of the factors is a power of 10.

Although any one of such factored forms may be more useful than the original form of the number, a special name is given to the last form. A number expressed as the product of a number between 1 and 10 (including 1) and a power of 10 is said to be in scientific form or scientific notation. For example,

4.18 x 10⁴ , 9.6 x 10², and 4 x 10⁵

are in scientific form.

Now, let us consider some factored forms of 0.0057 in which one of the factors is a power of 10.

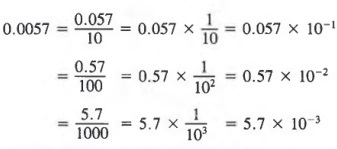
In this case, 5.7 x 10³ is the scientific form for 0.0057.

To write a number in scientific form:

1. Move the decimal point so that there is one nonzero digit to the left of the decimal point.
2. Multiply the result by a power of ten with an exponent equal to the number of places the decimal point was moved. The exponent is positive if the decimal point has been moved to the left and it is negative if the decimal point has been moved to the right.

Example 3

If a number is written in scientific form and we want to rewrite it in standard form, we simply reverse the above procedure.

Example 4

Common Error: Note that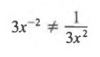

The exponent only applies to the x, not the 3. Thus,

CHAPTER SUMMARY

1. The quotient of two algebraic expressions is called a fraction. We can rewrite a quotient as a product by using the property

   A fraction can be changed from one form to another equivalent form by any of the following properties:

2. We can reduce fractions by using the following principles:

3. A fraction with a monomial denominator can be rewritten as follows:

   A fraction with a denominator that is a polynomial with two or more terms can be rewritten by using a method of long division.

4. We can build fractions by using the fundamental principle

   To change a/b to a fraction with denominator bc:

   1. Divide b into be to obtain the building factor c.
   2. Multiply numerator and denominator of the given fraction by the building factor c.

5. Powers a⁰ and a^-n are defined as follows:

   a⁰ = a (a ≠ 0)

   and

   A number expressed as the product of a number between 1 and 10 (including 1) and a power of 10 is said to be in scientific form or scientific notation. We use scientific notation to rewrite very large and very small numbers.