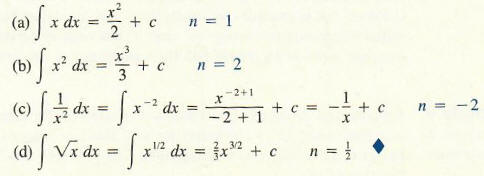INTEGRATION
This tutorial begins with a discussion of antiderivatives, mathematical objects that are closely related to derivatives. After the integral is introduced via the area problem, the integral and the antiderivative are shown to be related by an amazing theorem called the fundamental theorem of calculus. After establishing some techniques for evaluating integrals, we exhibit the important interpretation of the integral as a limit of a certain sum and demonstrate a variety of applications of the integral to problems in business and economics, geometry, and science.
Antiderivatives
Three examples of a type of problem that arises in various contexts are the following: find the cost function C (x) if marginal cost C '(x) is known; find the population P (t) of a biological colony if the rate P '(r) at which the population is changing is known; find the displacement s (t) of an object at time t if the velocity v (t) = s '(r) is known.
Notice that all these problems share the same basic format: to find f(x), given f '(x). All such problems are solved by antidifferentiation. An elementary example from business is the case of a manufacturer who determines that over an initial period of production. the marginal cost of production increases linearly and is given by C '(x) = 2x. We shall try to find a corresponding cost function C (x) for which C '(x) = 2x. Although we have no analytical procedures for finding such a C(x), it should be clear that the cost function C(x) = x2 will give us the known marginal cost C '(x) = 2x. But other cost functions will work as well. For example,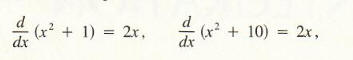
and in fact for any number a ,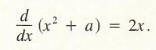
Thus, any cost function of the form C (x) = x2 + a will give the desired marginal revenue C '(x) = 2x; more information is needed to determine a specific value for a. We shall return to this in a moment. The process we are now considering is called antidifferentiation. In a general setting, it can be stated as follows:
Definition
For a given function f(x), a function g such that
is called an antiderivative of f. The process of finding such a function g is called antidifferentiation. Some mathematicians prefer to call this process indefinite integration, or simply integration for reasons that will become apparent in later sections.
In our introductory example, each of the cost functions x2, x2 + 1, and x2 + 10 is an antiderivative of f(x) = 2x; moreover, C(x) = x2 + a is an antiderivative of f(x) = 2x for any choice of a. In general, whenever g (x) is an antiderivative of f(x), so is g (x) + a for any number a, since
![]()
It is possible to prove the following even stronger result:
If g is any antiderivative of f, then every other antiderivative off must have the form g(x) + a for some number a.
Thus, we can think of g(x) + a as the most general antiderivative of f. Consequently, the most general antiderivative of f is not a single function but rather a class of functions g (x) + a that depend on a.
The German mathematician Gottfried Wilhelm Leibniz (1646-1716) introduced the notation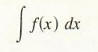
(read as "the antiderivative of f" or "the indefinite integral of f") to represent the most general antiderivative of f. Thus, if g is any antiderivative of f, then for any number a.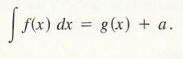
In summary:
Example 1

Example 2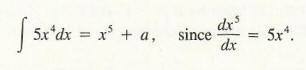
Example 3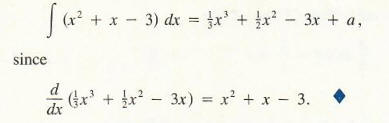
The number a that arises in antidifferentiation is often called an "arbitrary constant." (For reasons which will become apparent later, it is also called a "constant of integration.") In our examples we have used the letter a to designate this constant, but in practice c is usually used. (We used the letter a instead of c for our initial illustration involving cost since c was used to denote cost.) The following example gives us an insight into the significance of this arbitrary constant.
Example 4
Suppose that during the initial stages of production the marginal cost to produce a commodity is C '(x) = 2x dollars per unit. This time, suppose the manufacturer also knows that the fixed cost of production, C(0), is $500. Find the corresponding cost function C (x).
We have already seen that any cost function for this marginal cost must be of the form C(x) = x2 + a for some constant a. Since
C (0) = 500 = 02 + a = a,
we have a = 500. Thus, the cost function is given by C(x) = x2 + 500
From this example, we see that the arbitrary constant c is the fixed cost of production. Knowing only the marginal cost cannot tell us what that fixed cost is; the fixed cost is additional information. Each of the cost functions corresponding to a marginal cost of C'(x) = 2x will have the form
C(x) = x2 + (fixed cost).
The following two results are very useful in the evaluation of antiderivatives. Here, n denotes a real number and c is a constant of integration.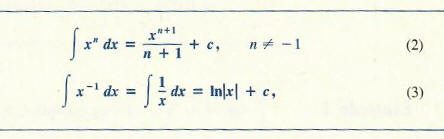
Note that Rule (2) holds for n != - 1. and Rule (3) covers the case that n = -1. To verify Rule (2), we use Definition (1) as follows:
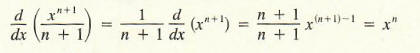
To verify Rule (3), recall that
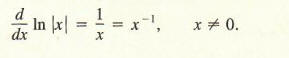
Example 5 Use Rule (2) to evaluate each antiderivative:
![]()
Solutions: