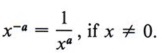Exponents and Radicals

Your work in algebra to this point has involved the four basic operations: addition, subtraction, multiplication, and division. In this chapter we will introduce the new operation of extracting roots, which is necessary to solve equations other than those of first degree. Since extracting roots is related to raising to powers, we will first review and expand the laws of exponents.

LAWS OF EXPONENTS, ZERO EXPONENTS, AND NEGATIVE EXPONENTS

OBJECTIVES

Upon completing this section you should be able to:

1. State the laws for positive integral exponents.
2. Modify these laws to include all integral exponents.

In chapter 7 we introduced and used the laws of exponents. We wish to review them here.

Here are some examples to refresh your memory.

Remember, y means y1. Note that only the quantity inside the parentheses is raised to the indicated power.

Now we will expand the concept of exponents to include all integers and not just the positive integers. If we pay special attention to law 3, we can see the reason for the definitions that follow.

We want to be able to use these laws for the integer zero and all the negative integers as well as the positive integers.

First let us use only that part of law 3 that states that and make no requirements as to the relative size of a and b. This will lead to two special cases, which in turn will require special definitions.

If, then, this law is to apply in this special case, we must make the following definition.

x⁰ = 1 for all numbers x except zero.

Note that x cannot be zero. Therefore 00 has no meaning.

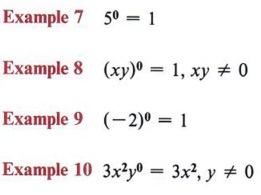
Now look at a problem such as 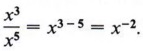. We already know by dividing like factors that . These two seemingly different answers to the same problem lead to the following definition.

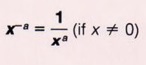
It is understood here that x can take on any value except 0. We will agree from this point on in all the examples and problems that the variables must never take on values that will give a meaningless expression. That means we cannot have a denominator equal to zero or a value of a variable that gives 00.

We can now write the third law of exponents simply as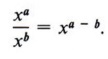

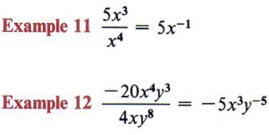
The laws of exponents will all apply to these new definitions. When working with negative exponents, be especially careful to use the laws of signed numbers properly.

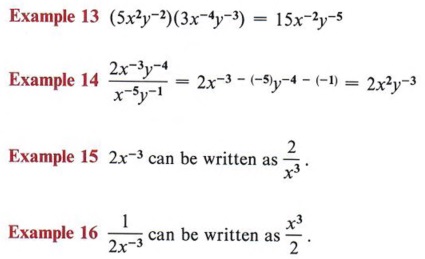
SCIENTIFIC NOTATION

OBJECTIVES

Upon completing this section you should be able to:

1. Identify a number that is in scientific notation.
2. Write a given number in scientific notation.
3. Change a number from scientific notation to one without exponents.
4. Perform computations using numbers in scientific notation.

Exponents are used in many fields of science to write numbers in what is called scientific notation. If a number is either very large or very small, this method of expressing it keeps it from being cumbersome and can make computations easier.

A number is in scientific notation if it is expressed as the product of a power of ten and a number equal to or greater than one and less than ten.

Notice that the definition is very explicit. The product must be of a number equal to or greater than one and less than ten, and a power of ten.

but this is not scientific notation because .93 is not equal to or greater than one.

To summarize: If the exponent is positive, the decimal point is moved to the right that number of places. If the exponent is negative, the decimal point is moved to the left that number of places.

Example 5 Write .0000000345 in scientific notation.

Solution Immediately we see that part of the answer must be 3.45 (equal to or greater than one and less than ten always gives one digit to the left of the decimal point).

If we now look at 3.45 we must ask, "What power of ten will return the decimal point to its original position?" Counting, we get eight places to the left, so

Scientific notation is useful in other ways than making numbers less cumbersome. Computations involving very large or very small numbers can be simplified because of the laws of exponents.

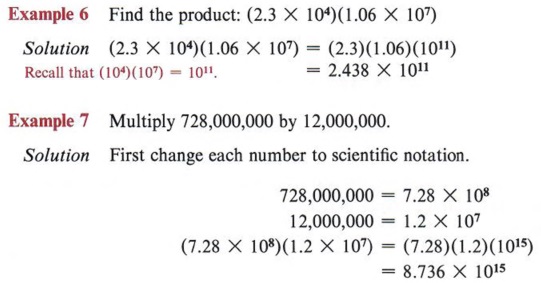
Most calculators cannot handle this problem in this form. A scientific calculator allows us to use scientific notation.

SIMPLIFYING SQUARE ROOTS

OBJECTIVES

Upon completing this section you should be able to:

1. State the definitions of square root and principal square root.
2. Guess the approximate value of the square root of a positive integer.
3. Simplify a square root radical.

In chapter 7 the symbol was defined to be the principal square root symbol. By way of review we will re-state the definitions concerning square root.

If x² = y, then x is a square root of y.

From this definition we have seen that every positive number has two square roots, one positive and one negative.

Recall these definitions from chapter 7.

The principal square root of a positive number is the positive square root.
The symbol is called a radical sign and indicates the principal square root of a number.

When these definitions were introduced and used in chapter 7, we were only interested in perfect square numbers such as 4, 9, 25, 81, 100, and so on. However, it is true that all positive numbers have two square roots. The square roots of numbers that are not perfect squares can be indicated by using the radical sign.

Although many people say "plus or minus," they really mean positive or negative.

The quantity under the radical sign is called the radicand.

Negative numbers have no square roots in the real number system. In elementary algebra the number system used is the set of real numbers, hence we say does not exist, or has no solution. In a more advanced study of algebra a set of numbers called the complex numbers will be introduced and, in that set, square roots of negatives will be defined. But for our present work, if the radicand is negative, state "no real solution."

The reason for this, of course, is that when you square any real number, you never get a negative number.

Square roots of positive numbers that are not perfect squares can be found correct to any number of decimal places by several methods. The "mechanical" or "rote" methods are based on algebraic concepts not yet developed in this book. Of course, the easiest method is to use a hand-held calculator and the next easiest method is to use a table such as the one printed on the inside back cover of this book.

Our purposes here do not require these estimations but you should have some concept as to the value of these numbers.

As an exercise, you will be asked to guess or estimate the value of some square roots and then check your guesses.

Now we wish to establish some facts about radicals. The following discussion leads to some important conclusions, so follow it carefully.

We now state these observations in general form.

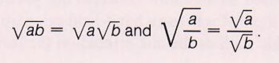
In words, "the square root of a product is the product of the square roots" and "the square root of a quotient is the quotient of the square roots."

This rule will be very useful in the following work.

A square root radical is in simplest form if no factor of the radicand is a perfect square.

We can now use this definition and the preceding rule to simplify square root radicals.

When writing a product of a numerical factor and a radical factor, indicate the radical last (that is,

If you obtain the factors 16 and 3 as the factors of 48 on your first try, you are lucky and will save an extra step or two.

From these examples it is evident that memorizing a list of perfect squares will speed your work. If a radical is to be in simplified form, no perfect square may be left under the radical.

You should know the squares of whole numbers up to at least 13.

An alternative method of finding all squares under the radical is especially useful for larger numbers.

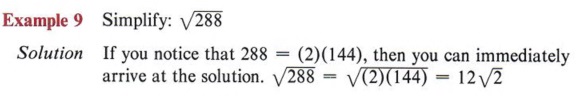
Always start by trying 2 as a divisor and keep dividing by 2 until it won't divide any more. Then do the same thing with the next prime number, 3, then 5, and so on, until you have all prime factors.

But suppose you did not recognize 288 as (2)( 144). Can you still arrive at the same solution? The answer is "yes" and the method is by completely factoring the radicand.
288 = (2)(2)(2)(2)(2)(3)(3)
which is the completely factored form. Now we have

and from the definition of square roots you can see that every pair of like factors under the radical give a perfect square (in other words,

In summary, simplify a square root radical by expressing the radicand as the product of two numbers, one of which is the largest perfect square factor. Or, if no such product comes to mind, factor the radicand completely and look for pairs of numbers that give perfect squares.

The same methods applied to the preceding exercises dealing with number rad-icands can be applied if the radicand contains letters or both numbers and letters. You must know, of course, that the letters cannot represent negative numbers.

Important! Unless otherwise stated, letters under radicands in this text will represent nonnegative real numbers.

Remember, nonnegative numbers refer to zero and the positive numbers. Again, try to find factors that are perfect squares.

OPERATIONS ON RADICALS

OBJECTIVES

Upon completing this section you should be able to:

1. Combine like radicals.
2. Multiply radical expressions.

In the preceding sections we have dealt with individual radicals. We now wish to discuss the basic operations on radicals.

Like square root radicals are square root radicals with the same radicand.

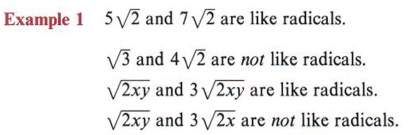
As we have stated several times, only like quantities may be combined.

To combine like radicals combine the coefficients and use this result as the coefficient of the common radical.

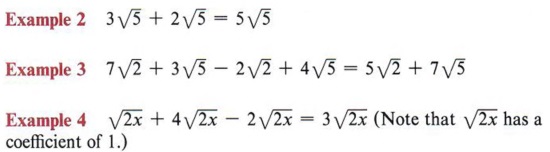
We can use the distributive property to show this. For example,

We cannot be sure that radicals are or are not like radicals unless they are in simplest form.

At first glance you might not realize that these radicals can be expressed as like radicals.

We have a rule that states . Using this rule and knowledge of multiplication, we can now multiply radical expressions.

Remember, we previously used the fact that

We remove parentheses by using the distributive property.

Do you recall the FOIL method?

SIMPLIFYING RADICAL EXPRESSIONS

OBJECTIVES

Upon completing this section you should be able to:

1. Simplify radical expressions whose denominator is a single radical.
2. Simplify expressions whose denominator is a binomial involving one or more radicals.

We now turn our attention to algebraic expressions that contain radicals. Our goal is to develop methods of simplifying such expressions.

Any algebraic expression which contains a radical is called a "radical expression."

A radical expression is in simplest form when two conditions are true.
(1) Each individual radical is in simplest form, and
(2) no radical appears in the denominator of a fraction.

Referring to the definition, we see that the first condition is met since are each in simplest form. However, the second condition is not met since we have a radical in the denominator.
To simplify such an expression we first appeal to the fundamental principal of fractions, which is stated as . We can multiply both numerator and denominator by the same nonzero number and still have a fraction equal to the original.

In the expression a radical is still in the denominator. What can we multiply this denominator by to remove the radical?

This process is known as rationalizing the denominator.

Why do we choose Because if we multiply 8 by 2 we get 16, which is a perfect square.

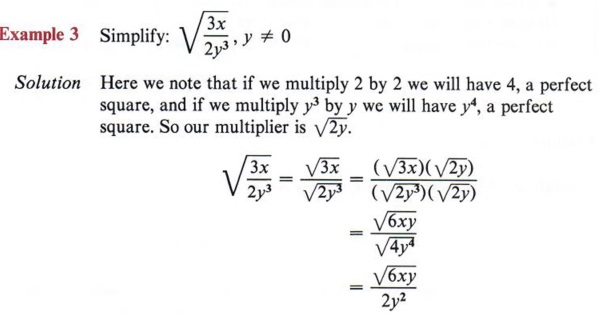
Solution It is easier to find the proper multiplier if you keep in mind the goal of building up the denominator to a perfect square. If we factor 27 into (3)(3)(3), we note that another (3) would give a perfect square. So the desired multiplier is

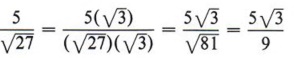
An alternate method of working this problem would be to first simplify the expression as Then we see that if we multiply the numerator and denominator by , we obtain

Again, we could have simplified first, obtaining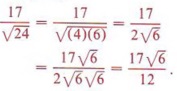

A very different problem is presented if the denominator is not a single radical.

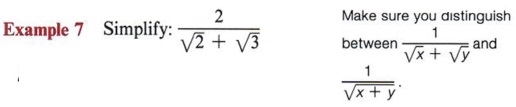
Solution Since we have a binomial in the denominator, we cannot multiply it by itself, for this will give a middle term that still contains a radical. We remember that the only time we can multiply a binomial by another binomial and not get a middle term is if we have the product of the sum and difference of the same two numbers. So the multiplier must be .

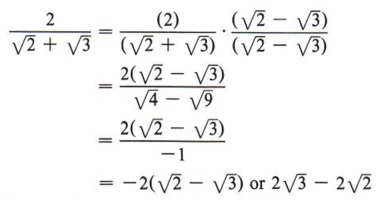
Note that if we try to multiply numerator and denominator by 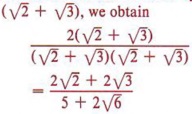and we are no better off than we were.

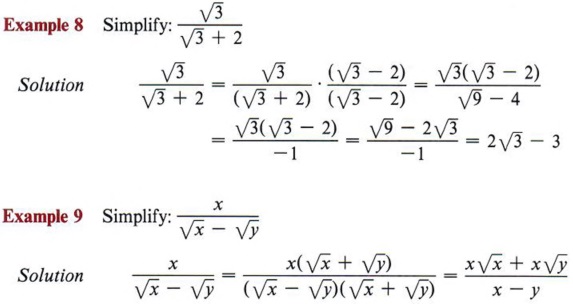
Again, make sure you don't get so involved in working with the denominator that you forget to also multiply the numerator.

SUMMARY

Key Words

• A zero exponent is defined as x⁰ = 1, if x ≠ 0.
• A negative exponent is defined as
  
• A number is in scientific notation if it is expressed as the product of a number equal to or greater than one but less than ten, and a power of ten.
• A radicand is the quantity under the radical sign.
• Like square root radicals are square root radicals with the same radicand.
• A radical expression is in simplest form if each radical is in simplest form and no radical appears in the denominator of a fraction.

Procedures

• To find the square root of a product use
  
• To find the square root of a quotient use
  
• To combine like radicals combine the coefficients and use this result as the coefficient of the common radical.
• To simplify a radical expression:
  1. Simplify each radical in the expression.
  2. Rationalize all denominators in the expression.