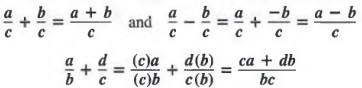OPERATIONS WITH FRACTIONS
PRODUCTS OF FRACTIONS
The product of two fractions is defined as follows.
The product of two fractions is a fraction whose numerator is the product of the numerators and whose denominator is the product of the denominators of the given fractions.
In symbols,
![]()
Any common factor occurring in both a numerator and a denominator of either fraction can be divided out either before or after multiplying.
Example 1 Find the product of ![]()
Solution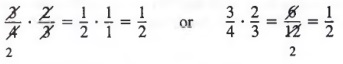
The same procedures apply to fractions containing variables.
Example 2 Find the product of ![]()
Solution First, we divide the numerator and denominator by the common factors to get
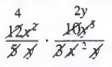
Now, multiplying the remaining factors of the numerators and denominators yields
![]()
If a negative sign is attached to any of the factors, it is advisable to proceed as if all the factors were positive and then attach the appropriate sign to the result. A positive sign is attached if there are no negative signs or an even number of negative signs on the factors; a negative sign is attached if there is an odd number of negative signs on the factors.
Example 3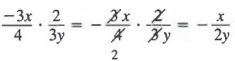
When the fractions contain algebraic expressions, it is necessary to factor wherever possible and divide out common factors before multiplying.
Example 4 Find the product of ![]() .
.
Solution First, we must factor the numerators and denominators to get
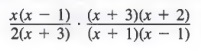
Now, dividing out common factors yields
![]()
We now multiply the remaining factors of the numerators and denominators to obtain
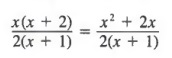
Note that when writing fractional answers, we will multiply out the numerator and leave the denominator in factored form. Very often, fractions are more useful in this form.
In algebra, we often rewrite an expression such as ![]() as an equivalent expression
as an equivalent expression ![]() .Use whichever form is most convenient for a particular problem.
.Use whichever form is most convenient for a particular problem.
Example 5![]()
Common Errors: Remember that we can only divide out common factors, never common terms! For example,
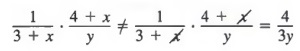
because x is a term and cannot be divided out. Similarly,
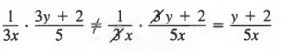
because 3 is not a factor of the entire numerator 3y + 2.
QUOTIENTS OF FRACTIONS
In dividing one fraction by another, we look for a number that, when multiplied by the divisor, yields the dividend. This is precisely the same notion as that of dividing one integer by another; a ÷ b is a number q, the quotient, such that bq = a.
To find ![]() , we look for a number q such that
, we look for a number q such that ![]() . To solve this equation for q, we multiply each member of the equation by
. To solve this equation for q, we multiply each member of the equation by ![]() . Thus,
. Thus,
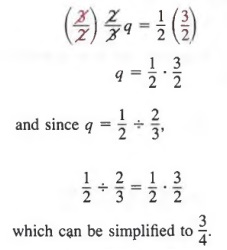
In the above example, we call the number ![]() the reciprocal of the number
the reciprocal of the number ![]() . In general, the reciprocal of a fraction
. In general, the reciprocal of a fraction ![]() is the fraction
is the fraction ![]() . That is, we obtain the reciprocal of a fraction by "inverting" the fraction. In general,
. That is, we obtain the reciprocal of a fraction by "inverting" the fraction. In general,
The quotient of two fractions equals the product of the dividend and the reciprocal of the divisor.
That is, to divide one fraction by another, we invert the divisor and multiply. In symbols,
![]()
Example 1
As in multiplication, when fractions in a quotient have signs attached, it is advisable to proceed with the problem as if all the factors were positive and then attach the appropriate sign to the solution.
Example 2
Some quotients occur so frequently that it is helpful to recognize equivalent forms directly. One case is
![]()
In general,
![]()
Example 3
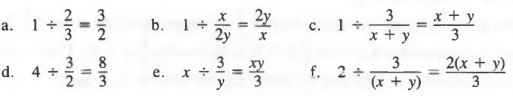
When the fractions in a quotient involve algebraic expressions, it is necessary to factor wherever possible and divide out common factors before multiplying.
Example 4

SUMS AND DIFFERENCES OF FRACTIONS WITH LIKE DENOMINATORS
The sum of two or more arithmetic or algebraic fractions is defined as follows:
The sum of two or more fractions with common denominators is a fraction with the same denominator and a numerator equal to the sum of the numerators of the original fractions.
In general,
![]()
Example 1
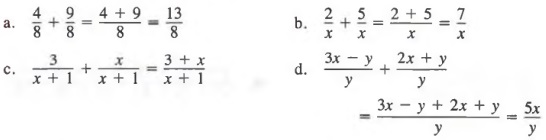
When subtraction is involved, it is helpful to change to standard form before adding.
Example 2
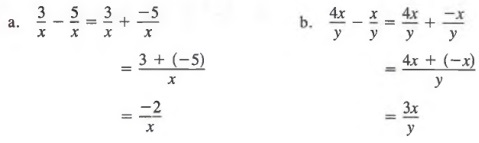
We must be especially careful with binomial numerators. For example, we should rewrite
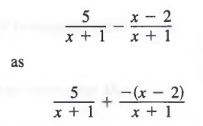
where the entire numerator is enclosed within parentheses.
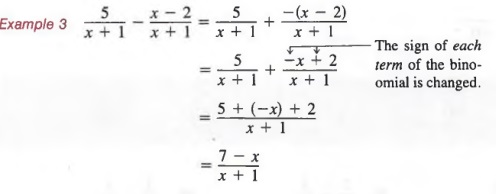
SUMS OF FRACTIONS WITH UNLIKE DENOMINATORS
In Section 6.3, we added fractions with like denominators. In this section, we will add fractions with unlike denominators.
LEAST COMMON DENOMINATOR
In general, the smallest natural number that is a multiple of each of the denominators of a set of fractions is called the lowest common denominator (LCD) of the set of fractions. Sometimes, we can obtain the LCD by inspection. If the LCD is not immediately evident, we can use a special procedure to find it.
To find the LCD:
- Completely factor each denominator, aligning common factors when possible.
- Include in the LCD each of these factors the greatest number of times it occurs in any single denominator.
Example 1 Find the lowest common denominator of the fractions ![]()
Solution The lowest common denominator for ![]() contains among its factors the factors of 12, 10, and 6.
contains among its factors the factors of 12, 10, and 6.

Thus, the LCD is 60. (This number is the smallest natural number that is divisible by 12, 10, and 6.)
The LCD of a set of algebraic fractions is the simplest algebraic expression that is a multiple of each of the denominators in the set. Thus, the LCD of the fractions
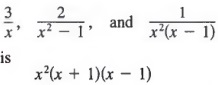
because this is the simplest expression that is a multiple of each of the denominators.
Example 2 Find the LCD of the fractions

Solution Following the method of Example 1, we get
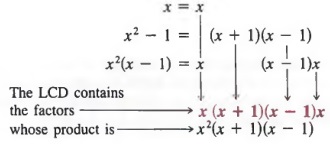
Thus, the LCD is x2(x + l)(x - 1).
We can add fractions with unlike denominators by first building the fractions to equivalent fractions with like denominators and then adding.
To add fractions with unlike denominators:
- Find the LCD of the set of fractions.
- Build each fraction to an equivalent fraction with the LCD as the denominator.
- Add the fractions using the property
![]()
Example 3 Write the sums of ![]() and
and ![]() as single terms.
as single terms.
Solution In each case, the LCD is 10. We build each fraction to a fraction with 10 as the denominator. Thus,
![]()
are equivalent to
![]()
from which we obtain
![]()
Sometimes, the fractions have denominators that are binomials.
Example 4 Write the sum of ![]() as a single term.
as a single term.
Solution The LCD is (x + 2)(x - 1). We build each fraction to a fraction with denominator (x + 2)(x - 1), inserting parentheses as needed, and get
![]()
Now that we have like denominators, we can add the numerators, simplify, and obtain
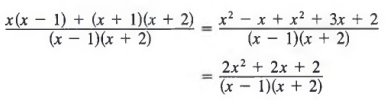
Example 5 Write the sum of ![]() as a single term.
as a single term.
Solution First we factor the denominators in order to obtain the LCD.
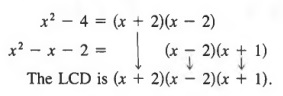
We now build each fraction to fractions with this denominator and get
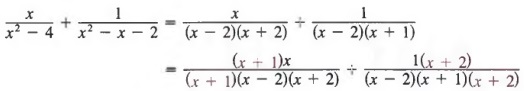
We can now add the numerators, simplify, and obtain
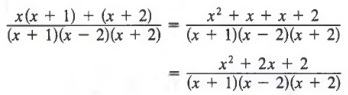
Common Errors Note that we can only add fractions with like denominators. Thus,
![]()
Also, we only add the numerators of fractions with like denominators. Thus,
![]()
DIFFERENCES OF FRACTIONS WITH UNLIKE DENOMINATORS
We subtract fractions with unlike denominators in a similar way that we add such fractions. However, we first write each fraction in standard form. Thus, any fraction in the form
![]()
is first written as
![]()
We can now add the fractions.
Example 1 Write the difference ![]() as a single term.
as a single term.
Solution We begin by writing ![]() in standard form as
in standard form as ![]() . The LCD is 12x. We build each fraction to an equivalent fraction with this denominator to get
. The LCD is 12x. We build each fraction to an equivalent fraction with this denominator to get
![]()
Now, adding numerators yields
![]()
Again, special care must be taken with binomial numerators.
Example 2 Write the difference of ![]() as a single term.
as a single term.
Solution ![]() should first be written as
should first be written as
![]()
where the entire numerator is enclosed within parentheses. Then, we obtain the LCD 6 and build each fraction to fractions with denominator 6, add numerators, and simplify.
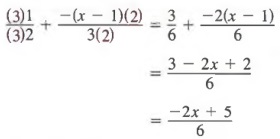
The next examples involve binomial denominators.
Example 3 Write the difference of ![]() as a single term.
as a single term.
Solution We begin by writing ![]() in standard form as
in standard form as ![]() . The LCD is (x - l)(x + 2) and we build each fraction to an equivalent fraction with this denominator to get
. The LCD is (x - l)(x + 2) and we build each fraction to an equivalent fraction with this denominator to get
![]()
Now adding numerators and simplifying yields
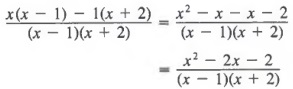
Example 4 Write the difference of
![]()
as a single term
Solution We first factor the denominators and write the fractions in standard form to get
![]()
We find the LCD (x + 7)(x - 3)(x + 3) and build each fraction to an equivalent fraction with this denominator to get
![]()
Now, adding numerators and simplifying yield
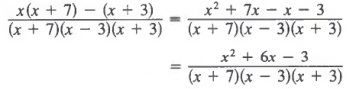
COMPLEX FRACTIONS
A fraction that contains one or more fractions in either its numerator or denominator or both is called a complex fraction. For example,
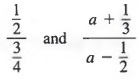
are complex fractions. Like simple fractions, complex fractions represent quotients. For example,
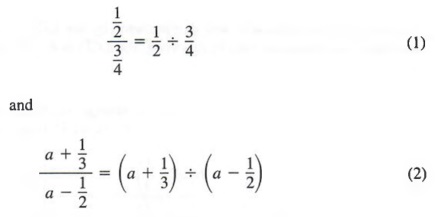
In cases like Equation (1), in which the numerator and denominator of the complex fraction do not contain sums or differences, we can simply invert the divisor and multiply. That is,
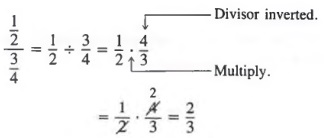
In cases like Equation (2), in which the numerator or denominator of the complex fraction contains sums or differences, we cannot simply invert the divisor and multiply. However, we can use the fundamental principle of fractions to simplify complex fractions. In fact, we can also use the fundamental principle to simplify complex fractions of Form (1) above.
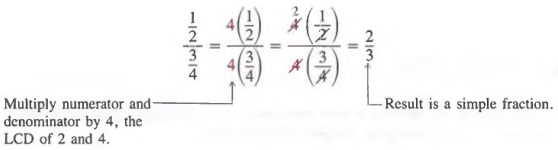
Example 1 Simplify ![]() by using the fundamental principle of fractions.
by using the fundamental principle of fractions.
Solution We multiply the numerator and denominator by the LCD of all fractions in the numerator and denominator; in this case, the LCD is 4. The result is a simple fraction equivalent to the given complex fraction.
The simplification of Equation (2) on page 255 appears in the next example.
Example 2 Simplify 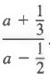
Solution We multiply the numerator and denominator by the LCD of all fractions in the numerator and denominator; in this case, the LCD is 6. We obtain

FRACTIONAL EQUATIONS
To solve an equation containing fractions, it is usually easiest to first find an equivalent equation that is free of fractions. We do this by multiplying each member of an equation by the lowest common denominator of the fractions.
Although we can apply the algebraic properties we have studied in any order, the following steps show the order most helpful in solving an equation when the solution is not obvious. Of course, not all the steps are always necessary.
To solve an equation:
- Clear fractions," if there are any, by multiplying each member of the equation by the LCD.
- Write any expression that contains parentheses as an expression without parentheses.
- Combine any like terms in either member.
- Obtain all terms containing the variable in one member and all terms not containing the variable in the other member.
- Divide each member by the coefficient of the variable if it is different from 1.
- Check the answer if each member of the equation has been multiplied by an expression containing a variable.
Example 1 Solve ![]() .
.
Solution We multiply each member by the LCD 15to obtain an equivalent equation that does not contain a fraction.
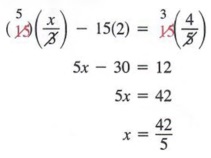
The multiplication property of equality (Section 3.4) allows us to multiply each member of an equation by a non zero value in order to obtain an equivalent equation. Thus, to solve the equation
![]()
we would multiply each member by the LCD 4(x - 5). We note that x cannot equal 5 since 4(x - 5) equals 0 if x = 5. The entire solution is shown in the next example.
Example 2 Solve ![]() .
.
Solution We multiply each member by the LCD 4(x - 5)to get
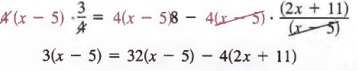
Applying the distributive property, we obtain
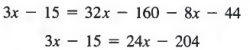
Solving for x yields
-21x = -189; x = 9
Note that 4(x - 5) is not equal to zero for a = 9. Thus, a = 9 is a valid solution for the equation.
When equations contain more than one variable, it is sometimes desirable to solve for one variable in terms of the other variable(s).
Example 3 Solve ![]() for a in terms of a, b, and c.
for a in terms of a, b, and c.
Solution We multiply each member by the LDC 3xc to get
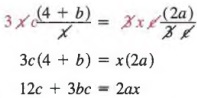
Now, dividing each member by 2x, we obtain
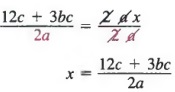
APPLICATIONS
The word problems in the following exercises lead to equations involving fractions. At this time, you may want to review the steps suggested to solve word problems and the steps suggested on page 260 to solve equations that contain fractions.
Example 1 If ![]() of a certain number is added to
of a certain number is added to ![]() of the number, the result is 11. Find the number.
of the number, the result is 11. Find the number.
Solution
Steps 1-2 We first write what we want to find (the number) as a word phrase. Then, we represent the number in terms of a variable.
The number: x
Step 3 A sketch is not applicable.
Step 4 Now we can write an equation. Remember that "of" indicates multiplication.![]()
Step 5 Solving the equation yields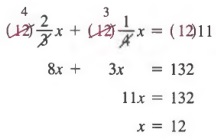
Step 6 The number is 12.
Equations for problems concerned with motion sometimes include fractions. The basic idea of motion problems is that the distance traveled d equals the product of the rate of travel r and the time of travel t. Thus, d = rt. We can solve this formula for r or t to obtain:
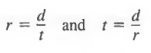
A table like the one shown in the next example is helpful in solving motion problems.
Example 2 An express train travels 180 miles in the same time that a freight train travels 120 miles. If the express goes 20 miles per hour faster than the freight, find the rate of each.
Solution Steps 1-2 We represent the two unknown quantities that we want to find as word phrases. Then, we represent the word phrases in terms of one variable.
Rate of freight train: r
Rate of express train: r + 20
Step 3 Next, we make a table showing the distances, rates, and times.

Step 4 Because the times of both trains are the same, we can equate the expressions for time to obtain ![]()
Step 5 We can now solve for r by first multiplying each member by the LCD r(r + 120) and we get
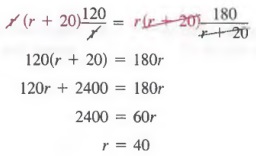
Step 6 The freight train’s speed is 40 mph and the express train’s speed is 40 + 20, or 60 mph.
RATIO AND PROPORTION
The quotient of two numbers, a ÷ b or ![]() , is sometimes referred to as a ratio and read "the ratio of a to b." This is a convenient way to compare two numbers.
, is sometimes referred to as a ratio and read "the ratio of a to b." This is a convenient way to compare two numbers.
Example 1 Express as a ratio.
a. 3 in. to 5 in.
b. 8 m to 12 m
c. 6 to 10
Solutions![]()
A statement that two ratios are equal, such as
![]()
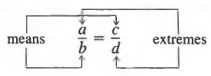
is called a proportion and read "2 is to 3 as 4 is to 6" and "a is to b as c is to d." The numbers a, b, c, and d are called the first, second, third, and fourth terms of the proportion, respectively. The first and fourth terms are called the extremes of the proportion, and the second and third terms are called the means of the proportion.
Example 2 Express as a proportion.
If each ratio in the proportion![]()
is multiplied by bd, we have
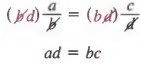
Thus,
![]()
In any proportion, the product of the extremes is equal to the product of the means.
A proportion is a special type of fractional equation. The above rule to obtain an equivalent equation without denominators is a special case of our general approach.
Example 3 Solve the proportion ![]() .
.
Solution By applying Property (1) above, we get
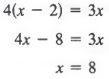
CONVERSIONS
We can use proportions to convert English units of measure into metric units and vice versa. The following basic relationships will be helpful in setting up appropriate proportions for conversions.
1 meter (m) = 39.37 inches (in.)
1 kilogram (kg) = 2.2 pounds (lb)
1 kilometer (km) = 0.62 miles (mi)
1 liter (1) = 1.06 quarts (qt)
1 pound (lb) = 454 grams (g)
1 inch (in.) = 2.54 centimeters (cm)
When converting units, it is easiest to follow the six steps outlined.
Example 4 Change 8 in. to centimeters.
Solution
Steps 1-2 Represent what is to be found (centimeters) in terms of a word phrase and in terms of a variable.
Centimeters: x
Step 3 Make a table showing the basic relationship between inches and centimeters.

Step 4 Using the table from Step 3, write a proportion relating inches to centimeters.
![]()
Step 5 Solve for x by equating the product of the means to the product of the extremes.
8(2.54) = 1 · x
20.32 = x
Step 6 Eight inches equals 20.32 centimeters.
CHAPTER SUMMARY
-
The following properties are used to rewrite products and quotients of fractions.
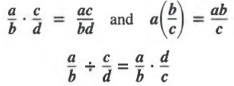
-
The smallest natural number that is a multiple of each of the denominators of a set of fractions is called the lowest common denominator (LCD) of the fractions. The following properties are used to rewrite sums and differences of fractions.
![]()
-
A fraction that contains one or more fractions in either numerator or denominator or both is called a complex fraction. We can simplify a complex fraction by multiplying the numerator and denominator by the LCD of all fractions in the numerator and denominator.
-
We can solve an equation containing fractions by obtaining an equivalent equation in which the solution is evident by inspection. Generally, it is best to obtain an equivalent equation that is free of fractions by multiplying each member of the equation by the LCD of the fractions.
-
The quotient of two numbers is called a ratio; a statement that two ratios are equal is called a proportion. In the proportion
![]()
a and d are called the extremes of the proportion and b and c are called the means. In any proportion of this form,
ad = bc