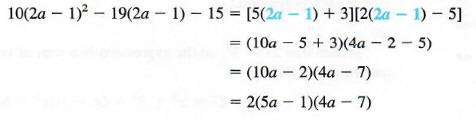FACTORING TRINOMIALS
Factoring is the opposite of multiplication. Since the product of two binomials is usually a trinomial, we can expect factorable trinomials (that have terms with no common factor) to have two binomial factors.Thus, factoring trinomials requires using FOIL backwards.
Factor each trinomial.
![]()
To factor this polynomial, we must find integers a, b, c, and d such that
4y^2 - 11y + 6 = (ay + b)(cy + d).
By using FOIL, we see that ac = 4 and bd = 6. The positive factors of 4 are 4 and 1 or 2 and 2. Since the middle term is negative, we consider only negative factors of 6. The possibilities are - 2 and - 3 or - 1 and - 6. Now we try various arrangements of these factors until we find one that gives the correct coefficient of y.
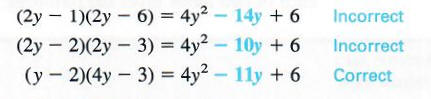
The last trial gives the correct factorization.
Factor
![]()
Again, we try various possibilities. The positive factors of 6 could be 2 and 3 or 1 and 6. As factors of - 5 we have only -1 and 5 or - 5 and 1. Try different combinations of these factors until the correct one is found.
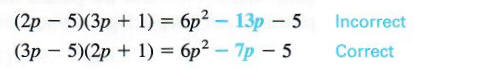
Finally, 6p^2 - 7p - 5 factors as (3p - 5)(2p + 1)
In the above examples, we chose positive factors of the positive first term. Of course, we could have used two negative factors, but the work is easier if positive factors are used.
Each of the special patterns of multiplication given earlier can be used in reverse to get a pattern for factoring. Perfect square trinomials can be factored as follows.
PERFECT SQUARE TRINOMIALS
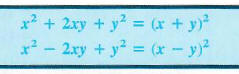
These formulas should be memorized.
Factor each polynomial.
![]()
Since 16p^2 = (4p)^2 and 25q^2 = (5q)^2, use the second pattern shown above with 4p replacing x and 5q replacing y to get
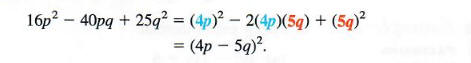
Make sure that the middle term of the trinomial being factored, -40pq here, is twice the product of the two terms in the binomial 4p - 5q.
FACTORING BINOMIALS
The pattern for the product of the sum and difference of two terms gives the following factorization.

Factor each of the following polynomials.
Example 1
![]()
First, recognize that 4m^2 - 9 is the difference of two squares, since 4m^2 =(2m)^2 and 9 = 3^2. Use the pattern for the difference of two squares with 2m replacing x and 3 replacing y. Doing this gives:
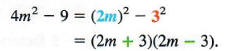
Example 2
![]()
Use the difference of two squares pattern twice, as follows:
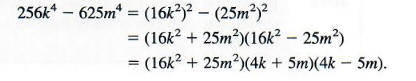
Example 3
![]()
Group the first three terms to get a perfect square trinomial. Then use the difference of squares pattern.
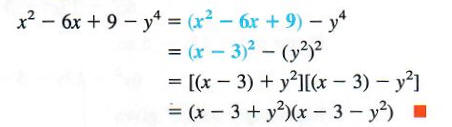
Two other special results of factoring are listed below. Each can be verified by multiplying on the right side of the equation.

Factor each polynomial.
Example 1
![]()
Notice that 27 = 3^3, so the expression is a sum of two cubes. Use the second pattern given above.
![]()
Example 2
![]()
Since 64n^3 = (4n)^3, the given polynomial is a difference of two cubes. To factor, use the first pattern in the box above, replacing x with m and y with 4n.
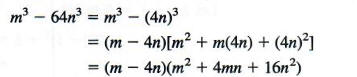
Example 3
![]()
Write 8q^6 as (2q^2)^3 and 125p9 as (5p^3)^3, so that the given polynomial is a sum of two cubes.
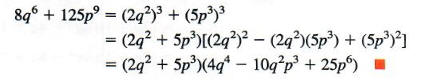
METHOD OF SUBSTITUTION
Sometimes a polynomial can be factored by substituting one expression for another. The next example shows this method of substitution.
Factor each polynomial.
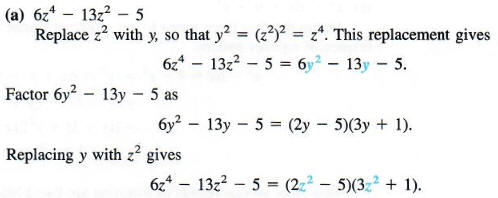
(Some students prefer to factor this type of trinomial directly using trial and error with FOIL.)
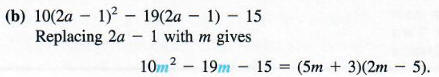
Now replace m with 2a - 1 in the factored form and simplify.