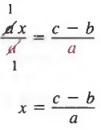FIRST-DEGREE EQUATIONS AND INEQUALITIES

In this chapter, we will develop certain techniques that help solve problems stated in words. These techniques involve rewriting problems in the form of symbols. For example, the stated problem

"Find a number which, when added to 3, yields 7"

may be written as:

3 + ? = 7, 3 + n = 7, 3 + x = 1

and so on, where the symbols ?, n, and x represent the number we want to find. We call such shorthand versions of stated problems equations, or symbolic sentences. Equations such as x + 3 = 7 are first-degree equations, since the variable has an exponent of 1. The terms to the left of an equals sign make up the left-hand member of the equation; those to the right make up the right-hand member. Thus, in the equation x + 3 = 7, the left-hand member is x + 3 and the right-hand member is 7.

SOLVING EQUATIONS

Equations may be true or false, just as word sentences may be true or false. The equation:

3 + x = 7

will be false if any number except 4 is substituted for the variable. The value of the variable for which the equation is true (4 in this example) is called the solution of the equation. We can determine whether or not a given number is a solution of a given equation by substituting the number in place of the variable and determining the truth or falsity of the result.

Example 1 Determine if the value 3 is a solution of the equation

4x - 2 = 3x + 1

Solution We substitute the value 3 for x in the equation and see if the left-hand member equals the right-hand member.

4(3) - 2 = 3(3) + 1

12 - 2 = 9 + 1

10 = 10

Ans. 3 is a solution.

The first-degree equations that we consider in this chapter have at most one solution. The solutions to many such equations can be determined by inspection.

Example 2 Find the solution of each equation by inspection.

a. x + 5 = 12
b. 4 · x = -20

Solutions a. 7 is the solution since 7 + 5 = 12.
b. -5 is the solution since 4(-5) = -20.

SOLVING EQUATIONS USING ADDITION AND SUBTRACTION PROPERTIES

In Section 3.1 we solved some simple first-degree equations by inspection. However, the solutions of most equations are not immediately evident by inspection. Hence, we need some mathematical "tools" for solving equations.

EQUIVALENT EQUATIONS

Equivalent equations are equations that have identical solutions. Thus,

3x + 3 = x + 13, 3x = x + 10, 2x = 10, and x = 5

are equivalent equations, because 5 is the only solution of each of them. Notice in the equation 3x + 3 = x + 13, the solution 5 is not evident by inspection but in the equation x = 5, the solution 5 is evident by inspection. In solving any equation, we transform a given equation whose solution may not be obvious to an equivalent equation whose solution is easily noted.

The following property, sometimes called the addition-subtraction property, is one way that we can generate equivalent equations.

If the same quantity is added to or subtracted from both members of an equation, the resulting equation is equivalent to the original equation.

In symbols,

a - b, a + c = b + c, and a - c = b - c

are equivalent equations.

Example 1 Write an equation equivalent to

x + 3 = 7

by subtracting 3 from each member.

Solution Subtracting 3 from each member yields

x + 3 - 3 = 7 - 3

or

x = 4

Notice that x + 3 = 7 and x = 4 are equivalent equations since the solution is the same for both, namely 4. The next example shows how we can generate equivalent equations by first simplifying one or both members of an equation.

Example 2 Write an equation equivalent to

4x- 2-3x = 4 + 6

by combining like terms and then by adding 2 to each member.

Combining like terms yields

x - 2 = 10

Adding 2 to each member yields

x-2+2 =10+2

x = 12

To solve an equation, we use the addition-subtraction property to transform a given equation to an equivalent equation of the form x = a, from which we can find the solution by inspection.

Example 3 Solve 2x + 1 = x - 2.

We want to obtain an equivalent equation in which all terms containing x are in one member and all terms not containing x are in the other. If we first add -1 to (or subtract 1 from) each member, we get

2x + 1- 1 = x - 2- 1

2x = x - 3

If we now add -x to (or subtract x from) each member, we get

2x-x = x - 3 - x

x = -3

where the solution -3 is obvious.

The solution of the original equation is the number -3; however, the answer is often displayed in the form of the equation x = -3.

Since each equation obtained in the process is equivalent to the original equation, -3 is also a solution of 2x + 1 = x - 2. In the above example, we can check the solution by substituting - 3 for x in the original equation

2(-3) + 1 = (-3) - 2

-5 = -5

The symmetric property of equality is also helpful in the solution of equations. This property states

If a = b then b = a

This enables us to interchange the members of an equation whenever we please without having to be concerned with any changes of sign. Thus,

If 4 = x + 2 then x + 2 = 4

If x + 3 = 2x - 5 then 2x - 5 = x + 3

If d = rt then rt = d

There may be several different ways to apply the addition property above. Sometimes one method is better than another, and in some cases, the symmetric property of equality is also helpful.

Example 4 Solve 2x = 3x - 9. (1)

Solution If we first add -3x to each member, we get

2x - 3x = 3x - 9 - 3x

-x = -9

where the variable has a negative coefficient. Although we can see by inspection that the solution is 9, because -(9) = -9, we can avoid the negative coefficient by adding -2x and +9 to each member of Equation (1). In this case, we get

2x-2x + 9 = 3x- 9-2x+ 9

9 = x

from which the solution 9 is obvious. If we wish, we can write the last equation as x = 9 by the symmetric property of equality.

SOLVING EQUATIONS USING THE DIVISION PROPERTY

Consider the equation

3x = 12

The solution to this equation is 4. Also, note that if we divide each member of the equation by 3, we obtain the equations

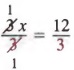
whose solution is also 4. In general, we have the following property, which is sometimes called the division property.

If both members of an equation are divided by the same (nonzero) quantity, the resulting equation is equivalent to the original equation.

In symbols,

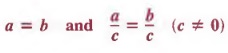
are equivalent equations.

Example 1 Write an equation equivalent to

-4x = 12

by dividing each member by -4.

Solution Dividing both members by -4 yields

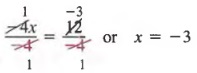
In solving equations, we use the above property to produce equivalent equations in which the variable has a coefficient of 1.

Example 2 Solve 3y + 2y = 20.

We first combine like terms to get

5y = 20

Then, dividing each member by 5, we obtain

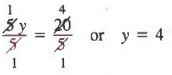
In the next example, we use the addition-subtraction property and the division property to solve an equation.

Example 3 Solve 4x + 7 = x - 2.

Solution First, we add -x and -7 to each member to get

4x + 7 - x - 7 = x - 2 - x - 1

Next, combining like terms yields

3x = -9

Last, we divide each member by 3 to obtain

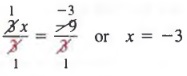
SOLVING EQUATIONS USING THE MULTIPLICATION PROPERTY

Consider the equation

The solution to this equation is 12. Also, note that if we multiply each member of the equation by 4, we obtain the equations

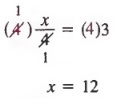
whose solution is also 12. In general, we have the following property, which is sometimes called the multiplication property.

If both members of an equation are multiplied by the same nonzero quantity, the resulting equation Is equivalent to the original equation.

In symbols,

a = b and a·c = b·c (c ≠ 0)

are equivalent equations.

Example 1 Write an equivalent equation to

by multiplying each member by 6.

Solution Multiplying each member by 6 yields

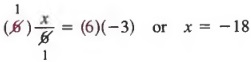
In solving equations, we use the above property to produce equivalent equations that are free of fractions.

Example 2 Solve

Solution First, multiply each member by 5 to get

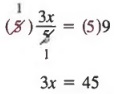
Now, divide each member by 3,

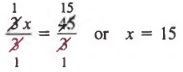
Example 3 Solve .

Solution First, simplify above the fraction bar to get

Next, multiply each member by 3 to obtain

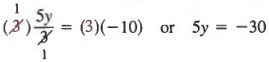
Last, dividing each member by 5 yields

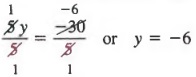
FURTHER SOLUTIONS OF EQUATIONS

Now we know all the techniques needed to solve most first-degree equations. There is no specific order in which the properties should be applied. Any one or more of the following steps listed on page 102 may be appropriate.

Steps to solve first-degree equations:

1. Combine like terms in each member of an equation.
2. Using the addition or subtraction property, write the equation with all terms containing the unknown in one member and all terms not containing the unknown in the other.
3. Combine like terms in each member.
4. Use the multiplication property to remove fractions.
5. Use the division property to obtain a coefficient of 1 for the variable.

Example 1 Solve 5x - 7 = 2x - 4x + 14.

Solution First, we combine like terms, 2x - 4x, to yield

5x - 7 = -2x + 14

Next, we add +2x and +7 to each member and combine like terms to get

5x - 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Finally, we divide each member by 7 to obtain

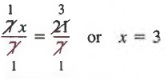
In the next example, we simplify above the fraction bar before applying the properties that we have been studying.

Example 2 Solve

Solution First, we combine like terms, 4x - 2x, to get

Then we add -3 to each member and simplify

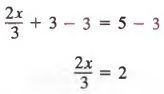
Next, we multiply each member by 3 to obtain

Finally, we divide each member by 2 to get

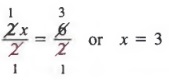
SOLVING FORMULAS

Equations that involve variables for the measures of two or more physical quantities are called formulas. We can solve for any one of the variables in a formula if the values of the other variables are known. We substitute the known values in the formula and solve for the unknown variable by the methods we used in the preceding sections.

Example 1 In the formula d = rt, find t if d = 24 and r = 3.

Solution We can solve for t by substituting 24 for d and 3 for r. That is,

d = rt

(24) = (3)t

8 = t

It is often necessary to solve formulas or equations in which there is more than one variable for one of the variables in terms of the others. We use the same methods demonstrated in the preceding sections.

Example 2 In the formula d = rt, solve for t in terms of r and d.

Solution We may solve for t in terms of r and d by dividing both members by r to yield

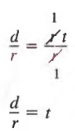
from which, by the symmetric law,

In the above example, we solved for t by applying the division property to generate an equivalent equation. Sometimes, it is necessary to apply more than one such property.

Example 3 In the equation ax + b = c, solve for x in terms of a, b and c.

Solution We can solve for x by first adding -b to each member to get

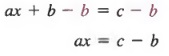
then dividing each member by a, we have