BASIC PROPERTIES OF MATRICES
A matrix having the same number of rows as columns is called a square matrix, The matrices below are square:
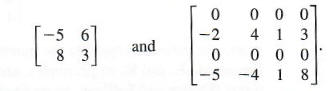
A matrix containing only one row is called a row matrix. Here are some examples:
[5 8], [6 -9 2], and [-4 0 0 0].
Finally, a matrix of only one column, as in part (d) of Example 1, is a column matrix.
It is customary to use capital letters to name matrices. Subscript notation is used to name the elements of a matrix, as follows.

Using this notation, the first row, first column element is denoted a11, the second row, third column element is denoted a23, and the ith row, jth column element is denoted aij.
Two matrices are equal if they are the same size and if each corresponding element, position by position, is equal. Using this definition, the matrices
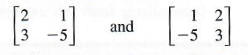
are not equal (even though they contain the same elements and are the same size), since the corresponding elements differ.
DECIDING WHETHER TWO MATRICES ARE EQUAL
Example 3
From the definition of equality given above, the only way that the statement
![]()
can be true is if 2 = x, 1 = y, p = -1, and q = 0.
The statement

can never be true, since the two matrices are different sizes. (One is 2 x 1 and the other is 3 x 1.)
ADDING MATRICES
At the beginning of this section we used the matrix

where the columns represent the numbers of cartons of three different types of vi tamins (A, E, and K, respectively), and the rows represent two different manufacturers (Dexter and Sullivan, respectively). For example, the element 7 represents 7 cartons of vitamin E pills from Dexter, and so on. Suppose another shipment from these two suppliers is described by the following matrix.

Here, for example, 8 cartons of vitamin K pills arrived from Sullivan. The number of cartons of each kind of pill that were received from these two shipments can be found from these two matrices.
In the first shipment, 2 cartons of vitamin A pills were received from Dexter,and in the second shipment, 3 cartons of vitamin A pills were received. Altogether, 2 + 3, or 5, cartons of these pills were received. Corresponding elements can be added to find the total number of cartons of each type of pill received.
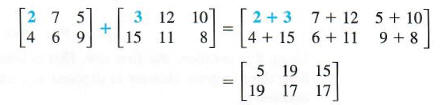
The last matrix gives the total number of cartons of each type of pill that were received. For example, 15 cartons of vitamin K pills were received from Dexter. Generalizing from this example leads to the following definition.
MATRIX ADDITION: The sum of two m x n matrices A and B is the m x n matrix A + B in which each element is the sum of the corresponding elements of A and B.
CAUTION: Only matrices of the same size can be added.
The matrices
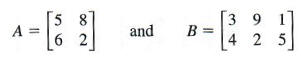
are different sizes. Therefore, the sum A + B does not exist.
A matrix containing only zero elements is called a zero matrix. For example, [0 0 0] is the 1 X 3 zero matrix, while

is the 2 X 3 zero matrix. A zero matrix can be written of any size.
In Chapter l the additive inverse of a real number a was defined as the real number -a such that a + (-a) = 0 and = a + a = 0. Given a matrix A, a matrix -A can be found such that A + (-A) = 0, where 0 is the appropriate zero matrix, and -A + A = 0. For example, if
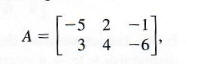
then the elements of matrix -A are the additive inverses of the corresponding elements of A. (Remember that each element of A is a real number and thus has an additive inverse.)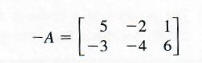
To check, first test that A + (-A) equals 0, the appropriate zero matrix.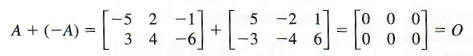
Then test that -A +A is also 0. Matrix -A is the additive inverse, or negative, of matrix A. Every matrix has a unique additive inverse.
SUBTRACTING MATRICES
Subtraction of real numbers was defined in Chapter L by saying that a - b = a + (-b). The same definition is used for subtraction of matrices.
If A and B are matrices of the same size, then
A - B = A + (-B)
Find each of the following differences.
The matrices

are different sizes and cannot be subtracted.
If a matrix A is added to itself, each element in the sum is twice as large as the corresponding element of A. For example,
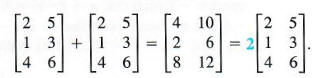
In the last expression, the number 2 in front of the matrix is called a scalar to distinguish it from a matrix. The example above suggests the following definition of multiplication of a matrix by a scalar.
MULTIPLICATION OF A MATRIX BY A SCALAR: The product of a scalar k and a matrix X is the matrix kX, each of whose elements is k times the corresponding element of X.
Find each product.