Example: (x^2-y^2)/(x-y)
To see your tutorial, please scroll down
Exponents and operations with polynomials
6.1 Exponents
To this point we have introduced the following properties of exponents.
If a is a nonzero integer and m and n are whole numbers, then
Property 1 a^m*a^n=a^(m+n)
Property 2 a^0=1
Property 3 a^n/a^m=a^(n-m) if n>=m
We will now extend Property 3 to include the case where n<m and introduce three more properties of exponents. All these properties are useful in simplifying algebraic expressions and operating (adding, subtracting, multiplying, and dividing) with algebraic expressions.
Consider the following examples :
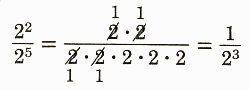
or 2^2/2^5=1/2^(5-2)=1/2^3
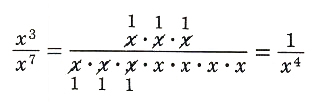
or x^3/x^7=1/x^(7-3)=1/x^4
We now complete Property 3 as follows:
Property 3 of Exponents
If a is a nonzero integer and m and n are whole numbers, then
a. a^n/a^m=a^(n-m) if n>=m
or b. a^n/a^m=1/a^(m-n) if n<m
Thus, in either case a or case b, the exponent for a will be positive or zero, but not negative. Negative exponents are discussed in Appendix I and in intermediate algebra.
Now consider an expression such as (2x)^3 where the base, 2x, is a product.
(2x)^3=(2x)*(2x)*(2x)
=2*2*2*x*x*x
=2^3*x^3=8x^3
Also, (3xy)^4=(3xy)*(3xy)*(3xy)*(3xy)
=3*3*3*3*x*x*x*x*y*y*y*y
=3^4*x^4*y^4=81x^4y^4
These examples lead to Property 4.
Property 4 of Exponents
If a and b are nonzero integers and n is a whole number, then
(ab)^n=a^(n)b^n
Fractions can be handled in a similar manner. For example,
(2/x)^3=2/x*2/x*2/x=(2*2*2)/(x*x*x)=2^3/x^3=8/x^3
((3x)/y)^4=(3x)/y*(3x)/y*(3x)/y*(3x)/y
=(3x*3x*3x*3x)/(y*y*y*y)=(3^4x^4)/y^4=(81x^4)/y^4
Property 5 of Exponents
If a and b are nonzero integers and n is a whole number, then
(a/b)^n=a^n/b^n
If a power is raised to a power, such as (2^2)^3 or (x^2)^5, we could write out the products, such as
(2^2)^3=2^2*2^2*2^2=2^(2+2+2)=2^6
(x^2)^5=x^2*x^2*x^2*x^2*x^2=x^(2+2+2+2+2)=x^10
But this process is time-consuming and can be handled in a more convenient way with Property 6.
Property 6 of Exponents
If a is a nonzero integers and m and n are whole numbers, then
(a^m)^n=a^(mn)
The following examples make use of all the various properties of exponents. Study the steps carefully. There may be more than one correct procedure to arrive at the simplified answer, but no properties of exponents are violated. You should apply the properties as they occur to you. Generally, there is no one best procedure.
Examples
1. (5x)^2=5^2*x^2=25x^2
2. (-3ab)^3=(-3)^3*a^3*b^3=-27a^3b^3
3. (y/x)^5=y^5/x^5
4. ((2x)/(3y))^2=(2x)^2/(3y)^2=(4x^2)/(9y^2)
5. (x^2)^4=x^(2*4)=x^8
6. (y^7)^2=y^(7*2)=y^14
7. ((-3a^5b)/(a^0b^9))^2(a^2/(2b))^3=((-3a^5)/b^8)^2(a^2/(2b))^3
=((-3a^5)^2)/((b^8)^2)*((a^2)^3)/((2b)^3)
=((-3)^2a^10)/(b^16)*a^6/(2^3b^3)=(9a^16)/(8b^19)
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
6.2 Division with Polynomials
The sum of fractions with common denominators can be written as a single fraction by adding the numerators and using the common denominator. For example,
3/a+(2b)/a+c/a=(3+2b+c)/a
Reversing the process, we can write
(3x^3+6x^2+9x)/(3x)=(3x^3)/(3x)+(6x^2)/(3x)+(9x)/(3x)=x^2+2x+3
Thus, we can express a single fraction with a monomial denominator as the sum of fractions with that denominator. This expression is sometimes preferred if some of the fractions can be simplified as we just did.
Similarly,
(x^2+2x+1)/x=x^2/x+(2x)/x+1/x=x+2+1/x
and (3x+6xy^2-9)/(3y)=(3xy)/(3y)+(6xy^2)/(3y)-9/(3y)=x+2xy-3/y
If we divide one polynomial by another, the quotient will be another polynomial with a remainder. The remainder must be of smaller degree than the divisor. If the remainder is 0, then the divisor and quotient are both factors of the dividend.
The long division procedure with a divisor that is not a monomial is illustrated step-by-step for
(3x^2-5x+4)/(x+2) or (3x^2-5x+4)÷(x+2)
Step 1.
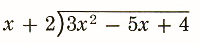
Write both polynomials in order of descending powers. If any powers are missing, fill in with 0’s.
Step 2.
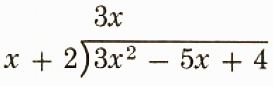
Mentally divide 3x^2 by x*(3x^2)/x=3x.
Write 3x above 3x^2.
Step 3.
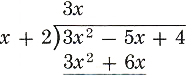
Multiply 3x times (x+2) and write the terms under the like terms in the dividend.
Step 4.
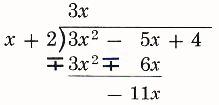
Subtract 3x^2+6x by changing signs and adding.
Step 5.
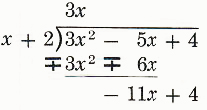
Bring down 4.
Step 6.
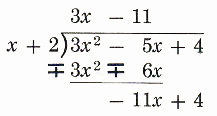
Mentally divide -11x by x. (-11x)/x=-11, Write -11 in the quotient directly above -11x.
Step 7.
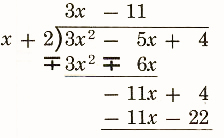
Multiply -11 times (x+2) and write the terms under like terms in the expression -11x+4.
Step 8.
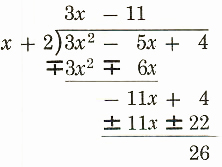
Subtract -11x-22by changing signs and adding. The remainder is 26.
Step 9.
Checking: Multiply the divisor and quotient and add the remain der; the result should be the dividend.
(3x-11)(x+2)+26=3x^2+6x-11x-22+26
=3x^2-5x+4
The answer can also be written in the form Q+R/D as 3x-11+26/(x+2)
The next example will be done in fewer steps. Follow the procedure closely.
(4x^3-7x+5)/(2x+1)
Step 1.
x^2 is missing power, so 0x^2 is supplied.
Step 2.
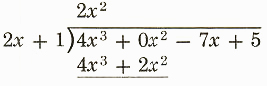
(4x^3)/(2x)=2x^2
2x^2(2x+1)=4x^3+2x^2
Step 3.
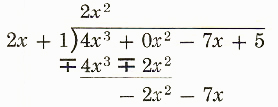
Subtract 4x^3+2x^2 and bring down -7x.
Step 4.
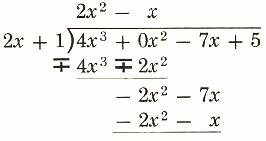
(-2x^2)/(2x)=-x Multiply -x times (2x+1).
Step 5.
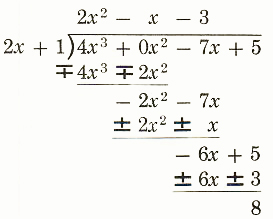
Continue dividing, using the same procedure. The remainder is 8.
Step 6.
Checking:
(2x+1)(2x^2-x-3)+8
=4x^3-2x^2-6x+2x^2-x-3+8
=4x^3-7x+5
The answer can also be written in the form
2x^2-x-3+8/(2x+1)
Let’s see how our polynomial solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
6.3 Multiplication and Division
Rational expressions are fractions that have polynomials for numerators and denominators. Some examples of rational expressions are:
x/(x^2+1),(x^2+5x+6)/(x^2+7x+12),(5a+3b)/(6a-b),(x-3)/(3-x),1/(5x)
To reduce a rational expression such as (x^2+5x+6)/(x^2+7x+12)numerator and denominator and “divide out" common factors, just as we did with fractions in Section 1.3. Thus,
(x^2+5x+6)/(x^2+7x+12)
= 
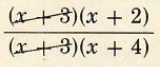
=(x+2)/(x+4)
The Fraction 15/17 cannot be reduced because 15 and 17 have no common factor other than +1 and -1. For the same reason, (x+2)/(x+4) cannot be reduced. That is, x+2 and x+4 have no common factor other than +1and -1. Trying to reduce a fraction such as (x+2)/(x+4) is a common mistake for beginning algebra students. You must remember: A fraction can be reduced only if the numerator and the denominator have a common factor. Common terms cannot be divided out. Only common factors can be divided out.
(x+2)/(x+4)!=2/4
but (5(x+2))/(5(x+4))=(x+2)/(x+4)
because 5 is a common factor.
Examples
Reduce each rational expression to lowest terms. No denominator can be 0.
1. (2x+4)/(3x+6)
=
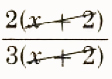
=2/3 (x!=-2)
2. (x^2-16)/(x+4)
=
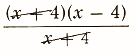
=x-4 (x!=-4)
3. a/(a^2-5a)
=
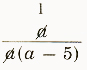
=1/(a-5) (a!=0,5)
4. (3-y)/(y-3)
=(-1(-3+y))/(y-3)
=
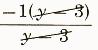
=-1 (y!=-3)
Note the important relationship illustrated in example 4:
(3-y)/(y-3)=-1
In general, for b!=a,
(a-b)/(b-a)=-1
because the numerator and denominator are opposite of each other. That is,
-(b-a)=-1(b-a)=-b+a=a-b
and -(a-b)=-1(a-b)=-a+b=b-a
Whenever this relationship occurs between a numerator and a denominator, the fraction can be reduced to -1.
(x-5)/(5-x)=-1 (x!=5)
(4-y)/(y-4)=-1 (y!=4)
Next, consider the three fractions
-6/2,6/-2 and -(6/2)
Are these equal? Yes! The negative sign can be With the numerator, with the denominator, or in front of the fraction, and the meaning or result will be the same.
-6/2=-3, 6/-2=-3, and -(6/2)=-3
In fact, We can make the following general statements
For integers a and b, b!=0,
-(a/b)=-a/b=a/-b
For polynomials P and Q, Q!=0,
-(P/Q)=-P/Q=P/-Q
At this stage of the discussion, we will assume that no denominator is 0. You should keep in mind that there are certain restrictions on the variable, but these restrictions will not be stated.
Examples
1. (x^2-16)/(4-x)
= 
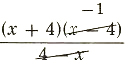
=(x+4)(-1)=-x-4
2. -((5-10x)/(2x-1))=-(5-10x)/(2x-1)
=
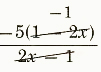
=-5(-1)=5
What do you think would be the product of (x+3)/x*(x-3)/(x+5)? Just as with fractions, multiply the numerators and multiply the denominators?
(x+3)/x*(x-3)/(x+5)=((x+3)(x-3))/(x(x+5))=(x^2-9)/(x^2+5x)
Any common factors should be “divided out" as in the following example.
(5x+15)/x^2*(x^2-3x)/(x^2-9)
=
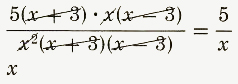
=5/x
If P,Q,R and S are polynomials with Q,S!=0, then
P/Q*R/S=(P*R)/(Q*S)
The quotient (x+2)/(x-1)÷(x^2-4)/(x^2-1)can be found by multiplying by the reciprocal of the divisor-again just as with fractions.
(x+2)/(x-1)÷(x^2-4)/(x^2-1)=(x+2)/(x-1)*(x^2-1)/(x^2-4)
=
If P,Q,R, and S are polynomials with Q,R,S!=0 then
P/Q÷R/S=P/Q*S/R
Examples
1. (x+5)/(7x)*(49x^3)/(x^2-25)
(x+5)/(7x)*(49x^3)/(x^2-25)
=
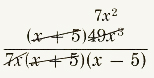
=(7x^2)/(x-5)
2. (a^2-49)/(12a^2)÷(a^2+8a+7)/(18a)
(a^2-49)/(12a^2)÷(a^2+8a+7)/(18a)=(a^2-49)/(12a^2)*(18a)/(a^2+8a+7)
=
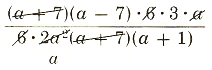
=(3(a-7))/(2a(a+1))
(Note: Generally, leaving the denominator factored as 2a(a+1) is more convenient than multiplying it out as 2a^2+2a)
Let’s see how our step by step polynomial solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
6.4 Addition and Subtraction
To add rational expressions with a common denominator, proceed just as with fractions: add the numerator and use the common denominator. For example,
5/(x+1)+6/(x+1)=(5+6)/(x+1)=11/(x+1)
Sometimes the sum can be reduced.
x^2/(x+1)+(2x+1)/(x+1)=(x^2+2x+1)/(x+1)=(x+1)^2/(x+1)=x+1
For polynomials P,Q, and R with Q!=0,
P/Q+R/Q=(P+R)/Q
To add 5/x^2+3/(x^2-4x), find a common denominator and change each fraction to an equal fraction with that denominator. The new denominator should be the least common multiple (LCM) of the original denominators. The LCM was discussed in Section 1.2 and Section 1.4. To find the LCM for a set of polynomials,
1. Completely factor each polynomial (including prime factors for numerical factors);'and
2. Form the product of all factors that appear using each factor the most number of times it appears in any one polynomial.
Thus, for the denominators x^2 and x^2-4x, we have
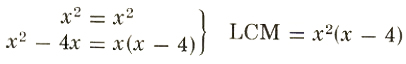
So x^2(x-4)is to be the common denominator:
5/x^2+3/(x^2-4x)=(5(x-4))/(x^2(x-4))+(3*x)/(x(x-4)*x)
=(5x-20)/(x^2(x-4))+(3x)/(x^2(x-4)
=(5x-20+3x)/(x^2(x-4))=(8x-20)/(x^2(x-4)
To subtract one rational expression from another with the same denominator, simply subtract the numerators and use the common denominator. Since the numerators will be polynomials, a good idea is to put both numerator in parentheses so that all changes in signs will be done correctly.
For example, many beginning students will make a mistake like the following:
7/(x+5)-(2-x)/(x+5)=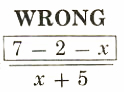
By using parentheses, such mistakes can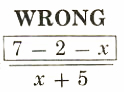55d6640c1393f09840c84c4a90.jpg" width="90" height="67" />=(7-2+x)/(x+5)=(5+x)/(x+5)=1
For polynomials P,Q, and R, with Q!=0,
P/Q-R/Q=(P-R)/Q
If the rational expressions do not have the same denominator, find the LCM of the denominators and change each fraction to an equal fraction with the LCM as denominator For example,
x/(x-1)-2/(x+1)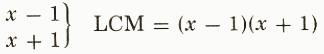 
x/(x-1)-2/(x+1)=(x(x+1))/((x-1)(x+1))-(2(x-1))/((x+1)(x-1))
=(x^2+x)/((x-1)(x+1))-(2x-2)/((x+1)(x-1))
=((x^2+x)-(2x-2))/((x-1)(x+1))=(x^2+x-2x+2)/((x-1)(x+1))
=(x^2-x+2)/((x-1)(x+1))
Another way to do the same problem is to place the negative sign with the numerator and add. The results are the same.
x/(x-1)-2/(x+1)=x/(x-1)+(-2)/(x+1)
=(x(x+1))/((x-1)(x+1))+(-2(x-1))/((x+1)(x-1))
=(x^2+x)/((x-1)(x+1))+(-2x+2)/((x+1)(x-1))
=(x^2+x-2x+2)/((x+1)(x-1))=(x^2-x+2)/((x+1)(x-1))
Examples
Perform the indicated operations and reduce if possible.
1. (x^2+5)/(x+5)+(6x)/(x+5)
(x^2+5)/(x+5)+(6x)/(x+5)
=(x^2+5+6x)/(x+5)
=(x^2+6x+5)/(x+5)
=
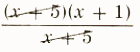
=x+1
2. 5/(x^2-1)+4/(x-1)^2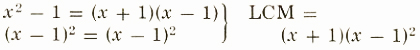 
5/(x^2-1)+4/(x-1)^2
=(5(x-1))/((x+1)(x-1)(x-1))+(4(x+1))/((x-1)^2(x+1))
=(5x-5+4x+4)/((x-1)^2(x+1))=(9x-1)/((x-1)^2(x+1))
3. (x+4)/(x+3)-(5x+1)/(x+3)
(x+4)/(x+3)-(5x+1)/(x+3)
=((x+4)-(5x+1))/(x+3)
=(x+4-5x-1)/(x+3)
=(-4x+3)/(x+3)
4. 3/(x-2)+5/(4-x^2) Factoring, 4-x^2 = (2+x)(2-x) and x-2=-1(2-x). Change the second fraction to avoid a factor of -1 in the denominator.
3/(x-2)+5/(4-x^2)
=3/(x-2)+(-5)/(x^2-4)
=(3(x+2))/((x-2)(x+2))+(-5)/((x+2)(x-2))
=(3x+6-5)/((x+2)(x-2))
=(3x+1)/((x+2)(x-2))
5. (2x)/(x^2-9)-1/(x^2+7x+12) x^2-9=(x+3)(x-3) x^2+7x+12=(x+4)(x+3) LCM=(x+3)(x-3)(x+4)
(2x)/(x^2-9)-1/(x^2+7x+12)
=(2x(x+4))/((x+3)(x-3)(x+4))+(-1(x-3))/((x+4)(x+3)(x-3)
=(2x^2+8x-x+3)/((x+3)(x-3)(x+4))
=(2x^2+7x+3)/((x+3)(x-3)(x+4))
=
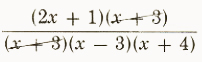
=(2x+1)/((x-3)(x+4))
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.