First-degree equations, inequalities and applications
7.1 First-Degree Equations
Equations are first-degree when they can be written in the form ax + b = c, where x is a variable and a, b, and c are known constants and a a!=0. We discussed the techniques for solving first-degree equations in Section 3.4 and again in Section 3.5 when dealing with formulas. Also, finding the solutions to proportions discussed in Sections 6.6 and 6.7 involved solving first-degree equations.
This topic is one of the most basic and important for any beginning algebra student and is presented again here for positive reinforcement and in preparation for solving a variety of applications in Sections 7.3, 7.4, and 7.5.
There is exactly one solution to a first-degree equation in one variable. This statement can be proved by the method of contradiction. The proof is not given here. Equations that have more than one solution will be discussed in Chapters 8, 9, and 10.
Examples
Solve the following equations.
1. 3x+14=x-2(x+1) Write the equation.
3x+14=x-2x-2 Use the distributive property to remove parentheses.
3x+14=-x-2 Simplify.
4x+14=-2 Add x to both sides.
4x=-16 Add -14 to both sides.
x=-4 Divide both sides by 4.
2. 1+2x+3-3x=20-x+6x Write the equation.
4-x=20+5x Simplify.
4=20+6x Add x to both sides.
-16=6x Add -20 to both sides.
-8/3=x Divide both sides by 6 and reduce.
3. (3x)/4-7=-1 Write the equation.
(3x)/4=6 Add +7 to both sides.
3x=24 Multiply both sides by 4.
x=8 Divide both sides by 3 and reduce.
Since (3x)/4=3/4*x/1=3/4x, we could solve an equation such as (3x)/4=6in one step by multiplying both sides by 4/3, the reciprocal of 3/4, as follows:
(3x)/4=6
(4/3*3/4)x=4/3*6
x=8
Example 3 can also be solved by multiplying first by 4 instead of adding +7 first. In this procedure, however, we must be sure to multiply each term by 4 on both sides of the equation.
(3x)/4-7=-1 Write the equation.
(3x)/4*4-7*4=-1*4 Multiply each term by 4.
3x-28=-4 Simplify.
3x=24 Add +28 to both sides.
x=8 Divide both sides by 3 and reduce.
This last technique has the advantage of leaving only integer coefficients and constants. If there is more than one fraction, then each term should be multiplied by the LCM of the denominators of the fractions.
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Example
(2x)/5+1/4=-(1/2)
(2x)/5*20+1/4*20=-(1/2)*20 Multiply each term by 20 the LCM of 5, 4, and 2.
8x+5=-10
8x=-15
x=-(15/8)
7.2 The Real Number Line and First-Degree Inequalities
We have discussed the integers, which include the whole numbers and their opposites,
...,-4,-3,-2,-1,0,1,2,3,4... (Integers)
and fractions formed using integers in the numerator and denominator with no denominator equal to 0. The formal name for such fractions is rational numbers. A rational number is any number that can be written in the form
a/b where a and b are integers and b!=0
In decimal form, all rational numbers can be written as repeating decimals. For example,
1/3=0.33333...
1/4=0.2500000... (repeats 0's)
1/7=0.142857142857142857...
and 5/3=1.66666...
Other forms of rational numbers are square roots of perfect square numbers. For example, since 5^2=25, the square root of 25 is 5 (Written root(25)=5). Also,
root(4)=2 since 2^2=4
-root(4)=-2 since (-2)^2=4
root(49)=7 since 7^2=49
-root(49)=-7 since(-7)^2=49
and root(4/9)=2/3 since (2/3)^2=4/9
The symbol √ is called a radical sign and the number under the radical sign is called the radicand.
Not all roots are integers or rational numbers. Numbers such as root(5),root(7),root(39), and -root(10) are called irrational numbers. In decimal form, all irrational numbers can be written as nonrepeating decimals. Other examples of irrational numbers are
root(2)=1.4142136... (square root of 2)
root(3,4)=1.5874011... (cube root of 4)
PI=3.14159265358979... (pi, ratio of circumference to diameter of a circle)
E=2.718281828459045... (base of natural logarithms)
Irrational numbers are just as important as rational numbers and just as useful in solving equations, as we will see in Chapter 10. Number lines have points corresponding to irrational numbers as well as rational numbers (See Figure 7.1).

Figure 7.1
Consider a circle with a diameter of 1 unit, rolling on a line. If the circle touches the line at the point 0, at what point on the line will the same point on the circle again touch the line?
The point will be at PI on the number line because PI is the circumference of the circle. (See Figure 7.2.)
Together the rational numbers and irrational numbers form the real numbers. That is, every rational number and every irrational number is also a real number. The properties of the real numbers under addition and multiplication are listed below Figure 7.2 on page 181.
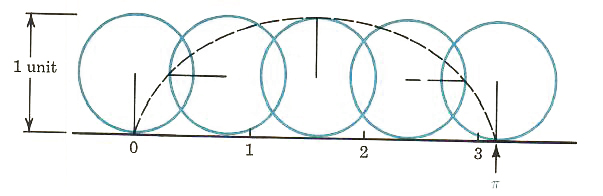
Figure 7.2
Properties of Real Numbers
For real numbers a,b, and c,
| Addition | Property | Multiplication |
| a+b is a real number | closure | a*b is a real number |
| a+b=b+a | commutative | a*b=b*a |
| a+(b+c)=(a+b)+c | associative | a*(b*c)=(a*b)*c |
| a+0=a | identity | a*1=a |
| a+(-a)=0 | inverse | a*1/a=1 (a!=0) |
Distributive property: a(b+c)=ab+ac
Number lines are now called real number lines because for every real number there is one corresponding point on a line, and for every point on a line there is one corresponding real number.
We are now interested in solving first-degree inequalities and graphing their solutions on a real number line. An inequality that can be written in the form ac+bor ax + b <= cwhere x is a variable and a,b, and c are constants and a!=0 is called a first-degree inequality.
Solving an inequality such as 2x + 1 < 7 is similar to solving a firstdegree equation. The object is to find an equivalent inequality (one with the same solutions) that is simpler in form.
2x+1<7
2x+1-1<7-1
2x<6
(2x)/2<6/2
x<3
 The shading indicates all real numbers less than 3. The open circle around 3 indicates 3 is not included in the graph.
The shading indicates all real numbers less than 3. The open circle around 3 indicates 3 is not included in the graph.
The important difference between solving equations and solving inequalities involves multiplying or dividing by negative numbers. Multiplying or dividing both sides of an inequality by a negative number reverses the sense of the inequality; “less than” becomes “greater than,” and vice versa. For example (arrows point out where inequalities are reversed)
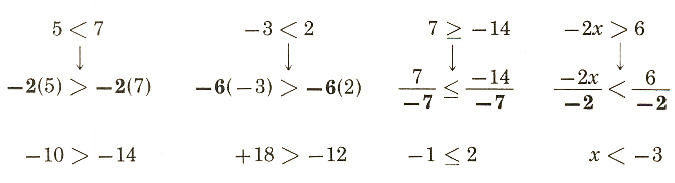
Solving a first-degree inequality depends on the following axiom:
1. If a nonzero constant is added to both sides of an inequality, the new inequality is equivalent to the original inequality.
2. If both sides of an inequality are multiplied by (or divided by) a positive constant, the new inequality of the same sense is equivalent to the original inequality.
3. If both sides of an inequality are multiplied by (or divided by) a negative constant, the new inequality of the opposite sense is equivalent to the original inequality.
Examples
Solve the following inequalities and graph the solutions
1. 5x+4<=-1 Write the inequality.
5x+4-4<=-1-4 Add -4 to both sides.
5x<=-5 Simplify.
(5x)/5<=-5/5 Divide both sides by 5.
x<=-1 Simplify.
 (Note: the solid dot means -1 is included.)
(Note: the solid dot means -1 is included.)
Let’s see how our inequality solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
2. x+1>=3-2x
x+1-x>=3-2x-x
1>=3-3x
1-3>=3-3x-3
-2>=-3x
-2/-3<=(-3x)/-3
2/3<=x

Alternative Procedure.
x+1>=3-2x
x+1+2x>=3-2x+2x
3x+1>=3
3x+1-1>=3-1
3x>=2
(3x)/3>=2/3
x>=2/3 Note that the two inequalities, 2/3<=x and x>=2/3, are identical in meaning.
We can also use the number line to graph numbers that satisfy more than one inequality. For example, 3 < x < 4 says that x is less than 4 and greater than 3. Also, x>=2 or x < 0 says that x is greater than or equal to 2 or less than 0. The graphs of these inequalities are shown below as examples.
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Examples
Graph the solutions to each of the following inequalities
1. 3 < x < 4 ![]()
2. x>=2 or x<0 ![]()
(Shading the circle around 2 indicates that 2 is included.)
3. -root(3)<x<root(2) ![]()
7.3 Applications (Distance, Geometry)
The difficulty or ease with which you solve a particular problem depends on many factors, including your personal experiences and general reasoning abilities. For example, suppose you were given the following problem:
“A car travels 170 miles in 3 hours. What was the average speed?”
The problem does not say directly to MULTIPLY, DIVIDE, ADD, or SUBTRACT. You must know that rate multiplied by time equals distance or, r*t=d. You are given the distance (170 miles) and the time (3 hours). You are to find the average speed. The tool you need is the formula r*t=d.
Let r = average speed. Then,
3*r=170
r=56*2/3mph
Example 1: Distance
A man leaves on a business trip, and at the same time his wife takes their children to visit their grandparents. The cars, traveling in opposite directions, are 360 miles apart at the end of 3 hours. If the man’s average speed is 10 mph more than his wife‘s, what is her average speed?
Let x = average speed of wife
rate*time=distance
| Wife | x | 3 | 3x |
| man | (x+10) | 3 | 3(x+10) |
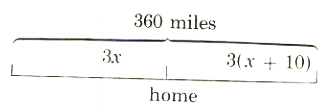
| distance for wife | + | distance for man | = | distance apart |
| 3x | + | 3(x+10) | = | 360 |
3x+3x+30=360
6x=330
x=55 mph
The wife’s average speed is 55 mph.
Example 2: Distance
Two trains, A and B, are 540 kilometers apart and travel toward each other on parallel tracks. Train A travels at 40 kilometers per hour and train Btravels at 50 kilometers per hour. In how many hours will they meet?
Let x = time
rate*time=distance
| train A | 40 | x | 40x |
| train B | 50 | x | 50x |
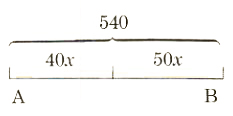
40x+50x=540
90x=540
x=6 hrs
The trains will meet in 6 hours.
Example 3: Geometry
A rectangle with a perimeter 140 meters has a length that is 20 meters less than twice the width. Find the dimensions of the rectangle.
Draw a diagram and use the formula P=2l+2w.
Let w= width
2w-20= length
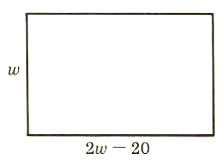
2(w)+2(2w-20)=140
2w+4w-40=140
6w=180
w=30 meters
2w-20=40 meters
The width is 30 meters and the length is 40 meters.
7.4 Applications (Interest, Work)
People in business know several formulas involving the principal (amount of money invested), rate (percent or rate of interest), and interest (the actual profit or interest earned). These formulas can depend on such related topics as the way the interest is paid on a loan (monthly, daily, yearly, etc.), whether or not there are penalties for early payment of a loan, or escalation clauses if an investment is particularly profitable.
In this section, we will use only the basic formula that calculates interest on an annual basis: P * R = {Iota}, or principal times rate equals interest.
Example 1: Interest
A man invests in a certain bond yielding 9% interest and then invests $500 in a high-risk stock yielding 12%. After one year, his total interest from the two investments is $240. What amount did he invest in the bond?
Let Pprincipal invested at 9%.
principal*rate=interest
| bond | P | 0.09 | 0.09P |
| high risk stock | 500 | 0.12 | 0.12(500) |
| interest on bond | + | interest on stock | = | total income |
| 0.09P | + | 0.12(500) | = | 240 |
0.09P+60=240
0.09P=180
(0.09P)/(0.09)=(180)/(0.09)
P=$2000
He invested $2000 in the bond yielding 9% interest.
Example 2: Interest
A woman has $7000. She decides to separate her funds into two investments. One yields an interest of 6% and the other, 10%. If she wants an annual income from the investments to be $580, how should she split the money?
Since we know the total to be invested is $7000, if one investment is $x, the other must be $7000- $x.
Let x = amount invested at 10%
7000 - x = amount invested at 6%
principal*rate=interest
| 10% investment | x | 0.10 |
0.10x |
| 6% investment | (7000-x) | 0.06 | 0.06(7000-x) |
| interest on 10% investment | + | interest on 6% investment | = | total income |
| 0.10x | + | 0.06(7000-x) | = | 580 |
10x+6(7000-x)=5800 Multiply each term by 100 to eliminate decimals.
10x+42000-6x=5800
4x=16000
x=$4000@10%
7000-x=$3000@6%
She should invest $4000 at 10% and $3000at 6%.
Problems involving “work” can be very sophisticated and require calculus and physics. The problems we will be concerned with relate to the time involved to complete the work on a particular job. These problems involve only the idea of what fraction of the job is done in one unit of time (hours, minutes, days, weeks, etc.). For example, if a man can dig a ditch in 4 hours, what part (of the ditch digging job) did he do in one hour? The answer is 1/4. If the job took 5 hours, he would do 1/5 in one hour. If the job took x hours, he would do 1/x in one hour.
Example 3: Work
Mike can clean his family’s pool in 2 hours. His younger sister, Stacey, can do it in 3 hours. If they work together, how long will it take them to clean the pool?
Let x = number of hours working together
| hours | part in 1 hour | |
| Mike | 2 | 1/2 |
| Stacey | 3 | 1/3 |
| together | x | 1/x |
| part done in 1 hr by Mike | + | part done in 1 hr by Stacey | = | part done in 1 hr together |
| 1/2 | + | 1/3 | = | 1/x |
1/2(6x)+1/3(6x)=1/x(6x) Multiply each term on both sides of the equation by 6x the LCM of the denominators.
3x+2x=6
5x=6
x=6/5hr
Together they can clean the pool in 6/5 hours, or 1 hour, 12 minutes.
Example 4: Work
A man was told that his new Jacuzzi pool would fill through an inlet valve in 3 hours. He knew something was wrong when the pool took 8 hours to fill. He found he had left the drain valve open. How long will it take to drain the pool?
Let t = time to drain pool.
(Note: In this case, the inlet and outlet valves work against each other.)
| hours | part in 1 hour | |
| inlet | 3 | 1/3 |
| outlet | t | 1/t |
| together | 8 | 1/8 |
| part filled by inlet | - | part emptied by outlet | = | part filled together |
| 1/3 | - | 1/t | = | 1/8 |
1/3(24t)-1/t(24t)=1/8(24t)
8t-24=3t
5t=24
t=24/5
The pool will drain in 24/5 hours, or 4 hours, 48 minutes.
7.5 Applications (Mixture, Inequalities)
Problems involving mixtures occur in physics and chemistry and in such places as a candy store or a tobacco shop. Two or more items of a different percentage of concentration of a chemical such as salt, chlorine, or antifreeze are to be mixed; or two or more types of tobacco are to be mixed to form a final mixture that satisfies certain conditions of percentage of concentration.
The basic plan is to write an equation that deals only with one part of the mixture. The following examples explain how this can be accomplished.
Example 1: Mixture
A particular experiment in chemistry demands a 10% solution of acid. If the lab assistant has 9 ounces of a 5% solution on hand, how much acid should be added to get the 10% solution? (Hint: Write an equation that deals only with amounts of acid.)
Let x = amount of acid to be added.
amount of solution ⋅ percent acid = amount of acid
| original solution | 9 | 0.05 | 0.05(9) |
| added solution | x | 1.00 | 1.00(x) |
| final solution | (x+9) | 0.10 | 0.10(x+9) |
| acid in 9 oz | + | acid added | = | acid in final solution |
| 0.05(9) | + | 1.00(x) | = | 0.10(x+9) |
5(9)+100(x)=10(x+9)
45+100x=10x+90 Multiply each term by 100.
90x=45
x=45/90
x=0.5 oz of acid
Check:
| acid in 9 oz | + | acid added | = | acid in final solution |
| 0.05(9) | + | 0.5 | = | 0.10(0.5+9) |
0.45+0.5=0.10(9.5)
0.95=0.95
The 10% solution can be had by adding 0.5 oz of acid.
Example 2: Mixture
How many gallons of a 20% salt solution should be mixed with a 30% salt solution to produce 50 gallons of 23% solution? (Hint: Write an equation that deals only with amounts of salt.)
Let x amount of 20% solution Note: Since the total number of gallons is known. one amount is found by subtracting the other amount from the total.
50-x = amount of 30% solution
amount of solution ⋅ percent salt = amount of salt
| 20% solution | x | 0.20 | 0.20x |
| 30% solution | 50-x | 0.30 | 0.30(50-x) |
| 23% solution | 50 | 0.23 | 0.23(50) |
| Salt in 20% solution | + | Salt in 30% solution | = | Salt in 23% solution |
| 0.20x | + | 0.30(50-x) | = | 0.23(50) |
20x+30(50-x)=23(50)
20x+1500-30x=1150
-10x=1150-1500
-10x=-350
x=35 gel of 20% solution
Check:
| Salt in 20% solution | + | Salt in 30% solution | = | Salt in 23% solution |
| 0.20(35) | + | 0.30(50-35) | = | 0.23(50) |
7.0+0.30(15)=11.5
7.0+4.5=11.5
11.5=11.5
Thirty-five gallons of the 20% solution should be added to 15 gallons of the 30% solution.
The following example using inequalities is self-explanatory. Study it carefully.
Example 3: Inequalities
A physics student has grades of 85, 98, 93, and 90 on four examinations. If he must average 90 or better to receive an A for the course, What scores can he receive on the final exam and get an A?
Let x = score on final exam.
(The average is found by adding the scores and dividing by 5.)
(85+98+93+90+x)/5>=90
(366+x)/5>=90
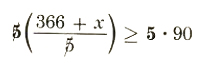
366+x>=450
x>=450-366
x>=84
If the student scores 84 or more on the final exam, he will average 90 or more and receive an A in physics.