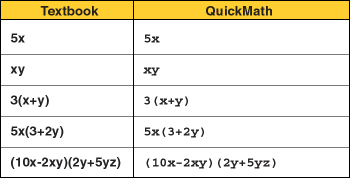
Here are some examples of typical expressions involving multiplication. This table shows you what they would look like in a textbook and how they would need to be entered for QuickMath.