Command Factor Expression
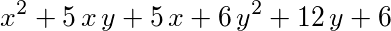 
- A sum consisting of 6 terms; the 1st term of the sum is equal to a power; the base is x; the exponent is two; the 2nd term of the sum is a product comprising 3 factors; the 1st factor of the product is equal to five; the 2nd factor of the product is x; the 3rd factor of the product is y; the 3rd term of the sum is equal to a product that comprises 2 factors; the 1st factor of the product is five; the 2nd factor of the product is x; the 4th term of the sum is equal to a product consisting of 2 factors; the 1st factor of the product is equal to six; the 2nd factor of the product is equal to a power; the base is y; the exponent is two; the 5th term of the sum is a product that consists of 2 factors; the 1st factor of the product is equal to twelve; the 2nd factor of the product is y; the 6th term of the sum is equal to six;
- x to the power of two plus five times x times y plus five multiplied by x plus six times y exponentiated by two plus twelve multiplied by y plus six.
Result
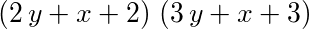 
- A product consisting of 2 factors. The 1st factor of the product is a sum containing 3 terms. The 1st term of the sum is equal to a product that contains 2 factors. The 1st factor of the product is equal to two. The 2nd factor of the product is equal to y. The 2nd term of the sum is x. The 3rd term of the sum is equal to two. The 2nd factor of the product is equal to a sum that comprises 3 terms. The 1st term of the sum is equal to a product comprising 2 factors. The 1st factor of the product is equal to three. The 2nd factor of the product is equal to y. The 2nd term of the sum is x. The 3rd term of the sum is equal to three.
- left parenthesis two times y plus x plus two right parenthesis times open bracket three times y plus x plus three close bracket.
|