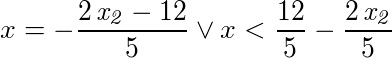Command Solve Inequality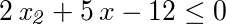 
- an inequality in which left side of inequality less than or equal to right side of inequality; the left side of the inequality is equal to a sum that contains 3 terms; the first term of the sum is a product of 2 factors; the first factor of the product is equal to two; the second factor of the product is equal to x 2-th; the second term of the sum is a product that comprises 2 factors; the first factor of the product is five; the second factor of the product is equal to x; the third term of the sum is negative twelve; the right side of the inequality is equal to zero;
- two times x 2-th plus five times x plus negative twelve smaller or equal than zero.
VariableResultA nonpolynomial inequality has been used, so the solution set may be incorrect. Exact 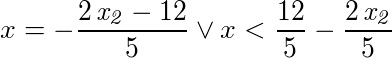 
- an inequality in which left side of inequality smaller than right side of inequality; the left side of the inequality is equal to x; the right side of the inequality is a sum of 2 terms; the first term of the sum is equal to a quotient: dividend of the quotient is twelve; divisor of the quotient is five; the second term of the sum is equal to a negative fraction: the top of the fraction is a product that contains 2 factors; the first factor of the product is two; the second factor of the product is equal to x 2-th; the bottom of the fraction is five;
- opening brace x less than twelve over five plus negative two multiplied by x 2-th over five closing brace.
Approximate
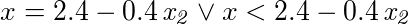 
- an inequality in which left side of inequality smaller than right side of inequality; the left side of the inequality is x; the right side of the inequality is a sum of 2 terms; the first term of the sum is two point four; the second term of the sum is a negative product comprising 2 factors; the first factor of the product is zero point four; the second factor of the product is x 2-th;
- opening bracket x less than two point four plus negative zero point and four tenth multiplied by x 2-th closing bracket;
|