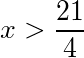QuickMath Download on App Store Download on Google Play
Welcome to Quickmath Solvers! Download on App Store Download on Google Play
Created on: 2012-01-08

A sample problem solved by Quickmath web math calculator

creating partial fractions from negative 29. | understand how to factor a product that comprises 2 factors; 12*x+30*y+36*z2

Command

Solve

Inequality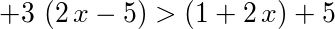
3*(2*x-5) > +(1+2*x)+5

  1. an inequality in which left side of inequality greater than right side of inequality; the left side of the inequality is equal to a product of 2 factors; the first factor of the product is equal to three; the second factor of the product is a sum containing 2 terms; the first term of the sum is a product that comprises 2 factors; the first factor of the product is equal to two; the second factor of the product is equal to x; the second term of the sum is equal to negative five; the right side of the inequality is equal to a sum of 2 terms; the first term of the sum is positive a sum containing 2 terms; the first term of the sum is equal to one; the second term of the sum is a product consisting of 2 factors; the first factor of the product is two; the second factor of the product is equal to x; the second term of the sum is five;
  2. three multiplied by opening bracket two times x plus negative five closing bracket larger than positive open parenthesis one plus two multiplied by x close parenthesis plus five;
Variable
Result

Exact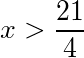

<<<<x > 21/4>>>>

  1. an inequality in which left side of inequality greater than right side of inequality; the left side of the inequality is x; the right side of the inequality is equal to a fraction: the numerator of the fraction is twenty one; the denominator of the fraction is four;
  2. left bracket left brace x greater than twenty one over four right brace right bracket.


Approximate

<<<<x > 5.25>>>>

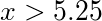
  1. an inequality in which left side of inequality greater than right side of inequality. The left side of the inequality is equal to x. The right side of the inequality is equal to five point two five.
  2. open parenthesis open parenthesis x greater than five point two five close parenthesis close parenthesis;