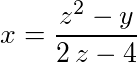QuickMath Download on App Store Download on Google Play
Welcome to Quickmath Solvers! Download on App Store Download on Google Play
Created on: 2011-12-05

A sample problem solved by Quickmath algebra calculator

the outcome of expanding log((x-5)^3)/((x+2)*(x-1)^2) | 3*y-3 > -y-11 inequality solved

Command

Solve

Equation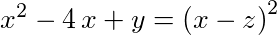
x^2-4*x+y = (x-z)^2

  1. an equation Left side of the equation is equal to a sum that comprises 3 terms; the first term of the sum is a power; the base is x; the exponent is two; the second term of the sum is a negative product that comprises 2 factors; the first factor of the product is equal to four; the second factor of the product is x; the third term of the sum is equal to y RHS is equal to a power; the base is a sum of 2 terms; the first term of the sum is equal to x; the second term of the sum is equal to negative z; the exponent is two;
  2. x to the power two plus negative four multiplied by x plus y is equal to opening bracket x plus negative z closing bracket raised to the power of two;
Variable
Result

Exact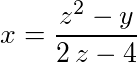

x = (z^2-y)/(2*z-4)

  1. an equation Left side of the equation is x RHS is equal to a fraction: the numerator of the fraction is a sum comprising 2 terms. The first term of the sum is a power. The base is z. The exponent is two. The second term of the sum is equal to negative y. The denominator of the fraction is a sum comprising 2 terms. The first term of the sum is equal to a product containing 2 factors. The first factor of the product is two. The second factor of the product is equal to z. The second term of the sum is negative four.
  2. x is equal to z raised to the power of two plus negative y over two times z plus negative four;