Command Factor Expression
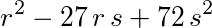 
- A sum that contains 3 terms. The first term of the sum is equal to a power. The base is r. The exponent is two. The second term of the sum is equal to a negative product consisting of 3 factors. The first factor of the product is equal to twenty seven. The second factor of the product is equal to r. The third factor of the product is equal to s. The third term of the sum is equal to a product containing 2 factors. The first factor of the product is seventy two. The second factor of the product is equal to a power. The base is s. The exponent is two.
- r raised to the power two plus negative twenty seven times r times s plus seventy two times s to the power two.
Result
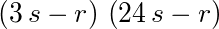 
- A product comprising 2 factors; the first factor of the product is equal to a sum containing 2 terms; the first term of the sum is a product that comprises 2 factors; the first factor of the product is equal to three; the second factor of the product is equal to s; the second term of the sum is equal to negative r; the second factor of the product is equal to a sum comprising 2 terms; the first term of the sum is equal to a product of 2 factors; the first factor of the product is equal to twenty four; the second factor of the product is s; the second term of the sum is equal to negative r;
- left parenthesis three times s plus negative r right parenthesis times opening parenthesis twenty four times s plus negative r closing parenthesis.
|