Addition and Subtraction of Polynomials

Addition of Polynomials

The sum of two specific numbers can be written as a third specific number. Given the specific numbers 2 and 3, we can write their sum as 2 + 3, or as 5.

The sum of the literal numbers a and b can merely be indicated as a + b. The a and b are called terms of the sum.

Terms that have identical literal factors are called like terms:  2abc, 3bac, -10cba are like terms. On the other hand, 2abc and 3abd are unlike terms, since 2abc has c as a factor while 3abd does not. The numerical coefficients of the terms do not affect whether the terms are like or unlike.

When the terms to be added are like terms, such as 5a and 7a, the sum 5a + 7a can be simplified by use of the distributive law of multiplication.

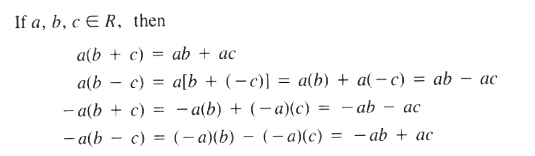
Using the distributive law of multiplication, we have

    5a + 7a = (5 + 7)a = 12a

Also 4a + a - 8a = (4+1)a - 8a

=5a - 8a

=(5 - 8)a

=- 3a

or 4a + a - 8a = (4 + 1 - 8)a

= -3a

It is important to realize that

    2a + 4a = (2 + 4)a = 6a

and 5a - 3a = (5-3)a = 2a (not just 2)

When we add polynomials, we combine only like terms in the polynomials

Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples solved step by step.

Example Add 3a - 5b and  -2a+2b

Solution (3a - 5b) + (-2a + 3b) = 3a - 5b - 2a + 3b

  =(3a - 2a) + (-5b + 3b)

  =(3-2)a + (-5 + 3)b = a - 2b

Example Add 3a - 2b + c and 6a + 4b - 5c

Solution (3a + 2b + c) + (6a + 4b -5c) = 3a - 2b +c +6a + 4b -5c

 =(3a + 6a) + (-2b + 4b) + (c -5c)

=(3 + 6)a + (-2 + 4)b + (1-5)c

=9a + 2b -4c

An easy way to find the sum of polynomials is to write the polynomials in rows one under the other, so that like terms are in the same column. This is similar to addition of

Specific numbers, when we write specific numbers in rows so that the units. tens, hundreds, and so forth are in separate columns.

Example Find the sum of the following polynomials

       2ab -6c +d 3c - 5d and 2d - 4ab +4c

Solution

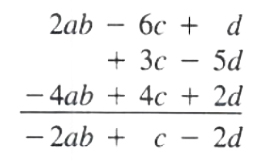
      (2ab - 6c +d) + (3c - 5d) + (2d - 4ab + 4c) = -2ab + c - 2d

Let's see how our Polynomial solver shows all the solution steps for this and similar problems. Click on "Solve Similar" button to see more examples.

Subtraction of Polynomials

In algebraic language we symbolize the subtraction of b from a by a - b, which is the same as a + (-b). That is. to subtract b from a, we add the additive inverse (the negative) of b to a.

The additive inverse of +6x is -6x. That is, -(+6x) = -6x.

The additive inverse of - 10y is + 10y. That is, -(-10y) = +10y

When the terms to be subtracted are like terms. the difference can be simplified using the distributive law of multiplication.

Example 1. Subtract (3a) from(8a)

         (8a) - (3a) = 8a - 3a = (8 - 3)a = 5a

2. Subtract (-3a) from (8a).

         (8a) - (-3a) = 8a + 3a = (8 + 3)a = 11a

3. Subtract (3a) from (-8a).

         (-8a) - (3a) = -8a - 3a = (-8 -3)a = -11a

4. Subtract (-3a) from (-8a).

         (-8a) - (-3a) = -8a + 3a = (-8 +3)a = -5a 

To subtract one polynomial, called the subtrahend, from another polynomial, called the minuend, add the minuend to the additive inverse of the subtrahend and combine like terms.

The additive inverse of a polynomial is the additive inverse of every term in the polynomial.

Subtraction of Polynomials

The additive inverse of 5a - 6b + 8 is -5a + 6b -8 That is,

      -(5a - 6b + 8) = -5a + 6b - 8

Example Subtract (3a - 5b) from (6a - 7b)

Solution (6a - 7b) - (3a - 5b) = 6a - 7b - 3a + 5b

=(6a - 3a) + (-7b + 5b)

=(6 - 3)a + (-7 +5)b

=3a - 2b

Let's see how our polynomial solver simplifies this problem step by step. Click on "Solve Similar" button to see more examples.

Example Subtract (3a - 2b + 5) from (8a + 6b -2)

Solution (8a + 6b -2) - (3a -2b +5) = 8a + 6b -2 -3a +2b -5

  =(8a -3a) + (6b +2b) + (-2 -5)

  =(8 -3)a + (6 +2)b + (-2 -5)

  =5a +8b -7

We can subtract polynomials more simply by writing them in rows. Write the minuend in the first row and the subtrahend in the second row, so that like terms are in the same column. The additive inverse of a polynomial is the same polynomial with the signs of the terms changed. Thus we change the signs of each term in the subtrahend. write the new signs in circles above the original signs, and add like terms using the new signs.

Example From 7ab -2c +8 subtract 8ab -5c +4

Solution  

      (7ab -2c +8) - (8ab -5c +4) = -ab +3c +4

Let's see how our Polynomial simplifier shows step by step solutions to  this and similar problems. Click on "Solve Similar" button to see more examples.

Example Subtract 2x - 3y - 6 from 4x - 3y +10

Solution 

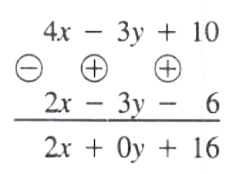
Since 0 , y = 0, that term does have to be written.

      (4x - 3y + 10) - (2x - 3y - 6) = 2x +16

Example Subtract 6ab + 2c -4 from 8ab -2b +3

Solution

      (8ab -2b +3) - (6ab + 2c - 4) = 2ab - 2b + 7 - 2c