Applications of Quadratic Equations

Application type problems are designed to teach you to read carefully, to think clearly, and to translate from English to algebraic expressions and equations. The problems do not tell you directly to add, subtract, multiply, divide, or square. You must decide on a method of attack from the wording of the problem combined with your previous experience and knowledge. Study the following examples and read the explanations carefully. They are similar to some, but not all, of the problems in the exercises.

       In a right triangle, one of the angles is a right angle (measures 90°) and the side opposite this angle (the longest side) is called the hypotenuse. Pythagoras was a famous Greek mathematician who is given credit for proving the following very important and useful theorem.

Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the two sides.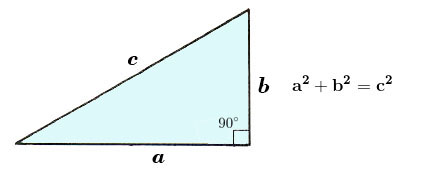

Example 1 illustrates how the Pythagorean Theorem can be used.

Example 1: The Pythagorean Theorem 

The length of a rectangle is 7 feet longer than the width. If one diagonal measures 13 feet, what are the dimensions of the rectangle?

Draw a diagram for problems involving geometric figures whenever possible.

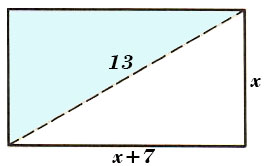
     Let x = Width of the rectangle

     x + 7 = length of the rectangle

(x+7)^2+x^2=13^2        Using the Pythagorean Theorem x^2+14x+49+x^2=169 2x^2+14x+49-169=0 2x^2+14x-120=0 2(x^2+7x-60)=0 2(x-5)(x+12)=0 x-5=0   or   x+12=0 x=5               x=-12

A negative number does not fit the conditions of the problem.

x=5ft width x+7=12ft length

Check:  5^2+12^2=13^2

            25+144=169

            169=169

The width is 5 ft and the length is 12 ft.

Now let's practice solving this type quadratic equation. This is how our quadratic solver would solve it step-by-step:

Example 2: Work

Working for a janitorial service, a woman and her daughter clean a building in 5 hours. If the daughter were to do the job by herself, she would take 24 hours longer than her mother would take. How long would it take her mother to clean the building without the daughter’s help?

          This problem is similar to the work problems discussed in previous section.

Let  x = time for mother alone

      x + 24 = time for daughter alone

1/x(5x)(x+24)+1/(x+24)(5x)(x+24)=1/5(5x)(x+24)    Multiply each term by the LCM of the denominators. 5(x+24)+5x=x(x+24) 5x+120+5x=x^2+24x 0=x^2+24x-10x-120 0=x^2+14x-120 0=(x-6)(x+20) x-6=0   or   x+20=0 x=6               x=-20

The value of x can't be negative for this problem.

So the mother could do the job alone in 6 hours.

Example 3: Distance, Rate, Time 

An airplane travels at a top speed of 200 mph. The plane, flying at top speed, is clocked over a distance of 960 miles and takes 2 hours more on the return trip because of a head Wind. (A tail wind was helping on the first leg of the flight.) What was the wind velocity?

     The basic formula is d = rt (distance = rate x time). Also, t = d/r; and r = d/t.

     If we know or can represent any two of the three quantities, the formula using these two should be used.

Let x = wind velocity

200 + x = speed going 200-x = speed returning 960 = distance each way

    We know distance and can represent rate (or speed), so the formula t = d/r is appropriate.

960/(200-x)(200-x)(200+x)-960/(200+x)(200-x)(200+x)=2(200-x)(200+x) 960(200+x)-960(200-x)=2(40000-x^2) 192000+960x-192000+960x=80000-2x^2 2x^2+1920x-80000=0 x^2+960x-40000=0 (x-40)(x+1000)=0 x-40=0   or   x+1000=0 x=40               x=-1000

The value of x can't be negative for this problem.

The wind velocity was 40 miles per hour.

Check: 960/(200-40)-960/(200+40)=2

            960/160-960/240=2

            6-4=2

            2=2

Example 4: Geometry

A square piece of cardboard has a small square, 2 in. by 2 in., cut from each corner. The edges are then folded up to form a box with a volume of 5000 cubic inches. What are the dimensions of the box? (Hint: The volume is the product of the length, width, and height. V = lwh.)

Draw a diagram illustrating the information.

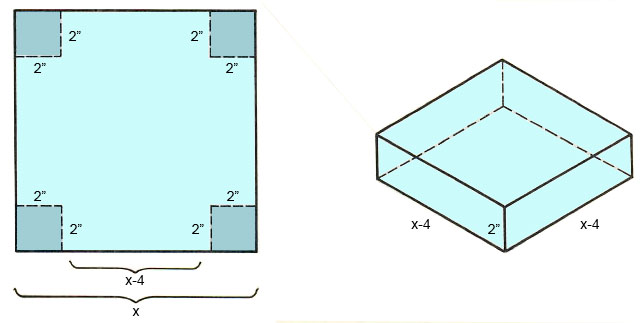
Let x = one side of the square.

2(x-4)(x-4)=5000 2(x^2-8x+16)=5000 x^2-8x+16=2500 x^2-8x-2486=0 (x-54)(x+46)=0 x-54=0   or   x+46=0 x=54            x=-46   The value of x can't be negative. x-4=50

Hence, The dimensions of the box are 50 in. by 50 in. by 2 in.