Example: 2x-1=y,2y+3=x
To see your tutorial, please scroll down
Common monomial factors, factoring special products and factoring polynomials
=9^3
=x^5
=1/1=1If a is a nonzero integer and m and n are whole numbers with n>=m, then
a^n/a^m=a^(n-m)
We will discuss this formula in more detail in Chapter 6.
Examples
Find the following quotients.
1. (24x^6)/(4x^4)=6x^(6-4)=6x^2
2. (-12a^3)/(3a)=-4a^(3-1)=-4a^2
3. (15a^4)/(5a^4)=3a^(4-4)=3a^0=3
By thinking of ab + ac as a product, we can find factors of ab + ac using the distributive property in a reverse sense as
ab+ac=a(b+c)
One factor is a and the other factor is b + c.
Applying this same reasoning to 2x^2 + 6x gives
2x^2+6x=2x*x+2x*3
=2x(x+3)
Note that 2x will divide into each term of the polynomial 2x^2 + 6x That is,
(2x^2)/(2x)=x and (6x)/(2x)=3
Finding the common monoinial factor in a polynomial means to choose the monomial with the highest degree and largest integer coefficient that will divide into each term of the polynomial. This monomial will be one factor and the sum of the various quotients will be the other factor. For example, factor
24x^6-12x^4-18x^3
On inspection, 6x^3 will divide into each term and
(24x^6)/(6x^3)=4x^3, (-12x^4)/(6x^3)=-2x, (-18x^3)/(6x^3)=-3
so 24x^6-12x^4-18x^3=6x^3(4x^3-2x-3)
With practice, all this work can be done mentally.
Examples
Factor the greatest common monomial in each polynomial.
1. x^3-7x=4(x^2-7) or x^3-7x=x*x^2+x(-7)=x(x-7)
2. 5x^3-5x^2-5x=5x(x^2-x-1)
3. -4x^5+2x^3-6x^2=-2x^2(2x^3-x+3)
If all the terms are negative or if the leading term (the term of highest degree) is negative, we will generally factor a negative common monomial, as in Example 3. This will leave a positive coefficient for the first term in parentheses.
All factoring can be checked by multiplying since the product of the factors must be the original polynomial.
A polynomial may be in more than one variable. For example, 5x^2y+10xy^2 is in the two variables x and y. Thus, a common monomial factor may have more than one variable.
5x^2y+10xy^2=5xy*x+5xy*2y
=5xy(x+2y)
Similarly,
4xy^3-2x^2y^2+8xy^2=2xy^2*2y+2xy^2(-x)+2xy^2*4
=2xy^2(2y-x+4).
(Note: (4xy^3)/(2xy^2)=2y, (-2x^2y^2)/(2xy^2)=-x, (8xy^2)/(2xy^2)=4)
Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
5.2 Factoring Special Products
In Section 4.4 we discussed the following special products of binomials
I. (x+a)(x+b)=x^2+(a+b)x+ab
II. (x+a)(x-a)=x^2-a^2 difference of two squares
III. (x+a)^2=x^2+2ax+a^2 perfect square trinomial
IV. (x-a)^2=x^2-2ax+a^2 perfect square trinomial
If we know the product polynomial, say x^2 + 9x + 20, we can find the factors by reversing the procedure. By having memorized all four forms, we recognize x^2 + 9x + 20 as in form I. We need to know the factors of 20 that add to be 9. They are 5 and 4 because 5*4 = 20 and 5 + 4 = 9. So, using form I,
x^2+9x+20=(x+5)(x+4)
Also, x^2-12x+20=(x-2)(x-10)
(-2)(-10)=20 and (-2)+(-10)=-12
and x^2-x-20=(x-5)(x+4)
(-5)(+4)=-20 and -5+4=-1
If the polynomial is the difference of two squares, we know from form II that the factors are the sum and difference of the terms that were squared.
x^2-a^2=(x+a)(x-a)
x^2-9=(x+3)(x-3)
x^2-y^2=(x+y)(x-y)
25y^2-4=(5y+2)(5y-2)
If the polynomial is a perfect square trinomial, then the last term must be a perfect square and the middle coefficient must be twice the term that was squared. (Note: We are assuming here that the coefficient of x^2 is 1. The case where the coefficient is not 1 will be covered in Section 5.3.) Using form III and form IV,
x^2+6x+9=(x+3)^2 9=3^2 and 6=2*3
x^2-14x+49=(x-7)^2 49=(-7)^2 and -14=2(-7)
Recognizing the form of the polynomial is the key to factoring. Sometimes the form may be disguised by a common monomial factor or by a rearrangement of the terms. Always look for a common monomial factor first. For example,
5x^2y-20y=5y(x^2-4) factoring the common monomial 5y
=5y(x+2)(x-2) difference of two squares
Examples
Factor each of the following polynomials completely.
1. x^2-x-12
x^2-x-12=(x-4)(x+3) -4(3)=-12 and -4+3=-1
2. y^2-10y+25
y^2-10y+25=(y-5)^2 perfect square trinomial
3. 6a^2b-6b
6a^2b-6b=6b(a^2-1) common monomial factor
=6b(a+1)(a-1) difference of two squares
4. 3x^2-15+12x
3x^2-15+12x=3(x^2-5+4x) common monomial factor
=3(x^2+4x-5) rearrange terms
=3(x+5)(x-1) -1(5)=-5 and -1+5=4
5. a^6-64 a^6=(a^3)^2
a^6-64=(a^3+8)(a^3-8) difference of two squares
Closely related to factoring special products is the procedure of completing the square. This procedure involves adding a square term to a binomial so that the resulting trinomial is a perfect square trinomial, thus “completing the square.” For example,
x^2+10x______ =(...)^2
The middle coefficient, 10, is twice the number that is to be squared. So, by taking half this coefficient and squaring the result, we will have the missing constant.
x^2+10x______ =(...)^2
x^2+10x+25=(x+5)^2 1/2(10)=5 and 5^2=25
For x^2+18x, we get
x^2+18x+____ =(...)^2
x^2+18x+81=(x+9)^2 1/2(18)=9 and 9^2=81
5.3 More on Factoring Polynomials
Using the FOIL method of multiplication discussed in Section 4.4, we can find the product
(2x+5)(3x+1)=6x^2+17x+5
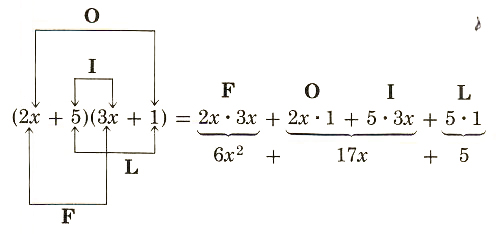
F: the product of the first two terms is 6x^2.
the sum of the inner and outer products is 17x.
L: he product of the last two terms is 5.
To factor the trinomial 6x^2 + 31x + 5 as a product of two binomials, we know the product of the first two terms must be 6x^2. By trial and error we try all combinations of factors of 6x^2, namely 6x and x or 3x and 2x, along with the factors of 5. This will guarantee that the first product, F, and the last product, L, are correct.
a. (3x+1)(2x+5)
b. (3x+5)(2x+1)
c. (6x+1)(x+5)
d. (6x+5)(x+1)
Now, for these possibilities, we need to check the sums of the inner and outer products to find 31x.
a.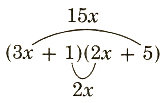 
15+2x=17x
b.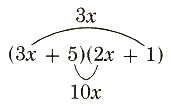 
3x+10x=13x
c.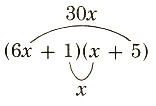 
30x+x=31x
We have found the correct combination of factors, so we need not try (6x + 5)(x + 1). So,
6x^2+31x+5=(6x+1)(x+5)
With practice the inner and outer sums can be found mentally and much time can be saved; but the method is still basically trial and error.
Examples
1. Factor 6x^2-31x+5
Solution:
Since the middle term is -31x and the constant is +5, we know that the two factors of 5 must be -5 and -1.
6x^2-31x+5=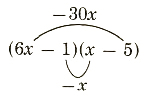
-30x-x=-31x
2. Factor 2x^2+12x+10 completely.
Solution:
2x^3+12x+10=2(x^2+6x+5) First find any common monomial factor.
=
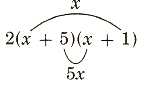x+5x=6x
Special Note: To factor completely means to find factors of the polynomial none of which are themselves factorable. Thus, 2x^2+12x+10=(2x+10)(x+1) is not factored completely since 2x + 10 = 2(x + 5). We could write
2x^2+12x+10=(2x+10)(x+1)=2(x+5)(x+1)
Finding the greatest common monomial factor first generally makes the problem easier. The trial-and-error method may seem difficult at first, but with practice you will learn to “guess” better and to eliminate certain combinations quickly. For example, to factor 10x^2+x-2, do we use 10x and x or 5x and 2x; and for -2, do we use -2 and +1 or +2 and -1? The terms 5x and 2x are more likely candidates since they are closer together than 10x and x and the middle term is small, 1x. So,
(5x+1)(2x-2) -10x+2x=-8x reject
(5x-1)(2x+2) +10x-2x=8x reject
(5x+2)(2x-1) -5x+4x=-x reject
(5x-2)(2x+1) 5x-4x=x reject
10x^2+x-2=(5x-2)(2x+1)
Not all polynomials are factorable. For example, no matter what combinations we try, 3x^2 - 3x + 4 will not have two binomial factors with integer coefficients. This polynomial is irreducible; it cannot be factored as a product of polynomials with integer coefficients.
An important irreducible polynomial is the sum of two squares, a^2 + b^2. For example, x^2 + 4 is irreducible. There are no factors with integer coefficients whose product is x^2 + 4.
Examples
Factor completely. Look first for the greatest common monomial factor.
1. 2x^2-50=2(x^2-25)=2(x+5)(x-5)
2. 6x^3-8x^2+2x=2x(3x^2-4x+1)=2x(3x-1)(x-1)
3. 2x^2+x-6=(2x-3)(x+2)
4. x^2+x+1=x^2+x+1 irreducible
Factoring polynomials with four terms can sometimes be accomplished by using the distributive law, as in the following examples.
Examples
1. xy+5x+3y+15=x(y+5)+3(y+5)
=(y+5)(x+3)
2. ax+ay+bx+by=a(x+y)+b(x+y)
=(x+y)(a+b)
3. x^2-xy-5x+5y=x(x-y)+5(-x+y)
This does not work because x-y!=-x+y.
Try factoring -5 instead of +5 from the last two terms.
x^2-xy-5x+5y=x(x-y)-5(x-y)
=(x-y)(x-5)
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.