Complex Algebraic Expressions & Proportions with Applications

6.5  Complex Algebraic Expressions

  An expression that contains various combinations of addition, subtraction, multiplication, and division with rational expressions is called a complex algebraic expression. Examples of complex algebraic expressions are:

  (1/x+1/y)/(x+y),(1/(x+2)-1/x)/(1+2/x) and (4-x)/(x+3)+x/(x+3)÷(x)/(x-3)

  In an expression such as (1/x+1/y)/(x+y), the large fraction bar is a symbol of inclusion. The expression could be written as follows:

  (1/x+1/y)/(x+y)=(1/x+1/y)÷(x+y)

Similarly, (1/(x+2)-1/x)/(1+2/x)=(1/(x+2)-1/x)÷(x+2/x)

  Simplify by working with the numerator and denominator separately as if they were in parentheses. Make the numerator a single fraction and the denominator a single fraction. Then divide.

  (1/x+1/y)/(x+y)=((1*y)/(x*y)+(1*x)/(y*x))/((x+y)/1)=((y+x)/(xy))/((x+y)/1)

  ==1/(xy)

  (1/(x+2)-1/x)/(1+2/x)=((1*x)/((x+2)x)-(1(x+2))/(x(x+2)))/(x/x+2/x)

  =((x-(x+2))/(x(x+2)))/((x+2)/x)=((x-x-2)/(x(x+2)))/((x+2)/x)

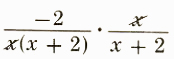  ==(-2)/((x+2)^2)

  A second method is to find the LCM of the denominators in the fractions in both the original numerator and the original denominator, and then multiply both the numerator and the denominator by this LCM.

  (1/x+1/y)/(x+y)=(1/x+1/y)/((x+y)/1)  x y 1  LCM=xy

  =((1/x+1/y)xy))/(((x+y)/1)xy)=(1/x*xy+1/y*xy)/((x+y)xy)

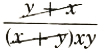  ==1/(xy)

  (1/(x+2)-1/x)/((1+2)/x)=((1/(x+2)-1/x)*x(x+2))/((1+2/x)*x(x+2)  x x+2  LCM=x(x+2)

  =

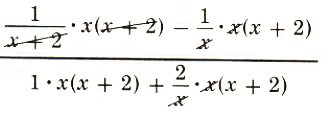
  =(x-(x+2))/(x(x+2)+2(x+2))=(x-x-2)/((x+2)(x+2))=(-2)/((x+2)^2)

  Each of the techniques just described is valid. Sometimes one is easier to use than the other, but the choice is up to you.

  In an expression such as

  (4-x)/(x+3)+x/(x+3)÷x/(x-3)

  the rules for order of operations indicate that the division is to be done first.

  (4-x)/(x+3)+x/(x+3)÷x/(x-3)

  =(4-x)/(x+3)+x/(x+3)*(x-3)/x

  =(4-x)/(x+3)+(x-3)/(x+3)

  =(4-x+x-3)/(x+3)

  =1/(x+3)

Example

  1. Simplify the following complex algebraic expression.

  (1/(x+y)-1/(x-y))/((2y)/(x^2-y^2))=((1(x-y))/((x+y)(x-y))-(1(x+y))/((x-y)(x+y)))/((2y)/(x^2-y^2))

  =(((x-y)-(x+y))/((x-y)(x+y)))/((2y)/(x^2-y^2))=(x-y-x-y)/((x-y)(x+y))*(x^2-y^2)/(2y)

  =

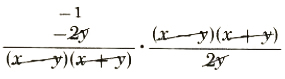
  =-1

  Or, using the technique of multiplying the numerator and the denominator by the LCM of the denominators of the various fractions,

  (1/(x+y)-1/(x-y))/((2y)/(x^2-y^2))=((1/(x+y)-1/(x-y))(x+y)(x-y))/(((2y)/(x^2-y^2))(x+y)(x-y)

  =

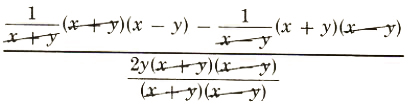
  =((x-y)-(x+y))/(2y)

  =(x-y-x-y)/(2y)

  =(-2y)/(2y)

  =-1

Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

6.6  Proportions with Applications

  Consider the statement, “At that university, there are two male students for every three female students.” Does this mean there are only 5 students, 2 of which are men and 3 are women? Not very likely. Suppose the odds on a horse race are 10 to 1 on Old Blue. If Old Blue wins and you bet $2, what do you win?

  These are examples of ratios. A ratio is a comparison of two numbers, usually Written as a:b or a/b. The ratio of men to women students can be written 2:3 or 2/3 The ratio of dollars payoff to dollars bet on Old Blue would be 10:1 or 10/1.

  We are interested in proportions. A proportion is an equation that states two ratios are equal. Examples are

  3/4=6/8, 10/1=x/2, (3n)/(5n)=3/5, and (x+3)/2=(x-5)/4

  Is the proportion 6/10=9/15 true ? One way to answer this question is to reduce both fractions.

  6/10=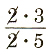=3/5 and 9/1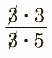5==3/5

  So, 6/10=9/15 is true.

  Another technique is to note 6*15=10*9 or 6*15=90and 10*9=90. We say the product of the extremes is equal to the product of the means. The following format can be used in identifying the extremes and means of a proportion.

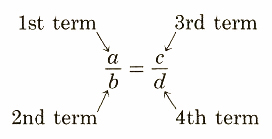
  a and d (the lst and 4th terms) are called the extremes; b and c (the 2nd and 3rd terms) are called the means.

  If a/b=c/d, then a*d=b*c

  This relationship can be shown in the following way.

    a/b=c/d

  a/b*(bd)/1=c/d*(bd)/1  Multiply both sides by bd.

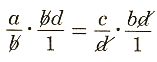    Simplify.

  a*d=b*c

  If one or more of the terms is not known, the equation should be solved to find a value for the unknown represented in the terms. The first step should be to find the product of the means and the product of the extremes and set these equal to each other.

Examples

  Solve the following proportions for the unknown number

  1. 12/15=8/x

   12x=15*8

   (12x)/12=(15*8)/12

   x=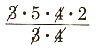=10

  Or, reducing 12/15 first to 4/5:

   12/15=8/x

   4/5=8/x

   4x=5*8

   (4x)/4=40/4

   x=10

  2. (x+3)/2=(x-5)/4

   4(x+3)=2(x-5)

   4x+12=2x-10

   4x+12-2x-12=2x-10-2x-12

   2x=-22

   (2x)/2=-22/2

   x=-11

Check:

   (-11+3)/2=(-11-5)/4

   -8/2=-16/4

   -4=-4

Let’s see how our equation solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  Proportions arise naturally in everyday problems. For example, if tires are on sale at 2 for $75 but you need 5 new tires, what would you pay for the 5 tires? Setting up a proportion gives:

  Solving,

    2/75=5/x

    2x=5*75

    (2x)/2=375/2

    x=$187.50

  The cost of 5 tires would he $187.50.

Example

  1. On an architect's scale drawing of a building, 1/2 inch represents 12 feet What does 3 inches represent?

  Solution:

   (1/2inch)/(12 feet)=(3 inches)/(x feet)

   1/2x=3*12

   2*1/2x=36*2

   x=72

  Three inches represents 72 feet.