Equation of Circle and Parabolas
7.5 The Equation of a Circle
A circle C in the XY plane, with center at the point (h, k) and radius r, is the set of all points at distance r from the point (h, k). Let P: (x,y) be any point on C. Then by the distance formula from Section 7.1 we have
root((x-h)^2+(y-k)^2)=r
An equivalent equation is
(1) (x-h)^2+(y-k)^2=r^2
See Figure 7.
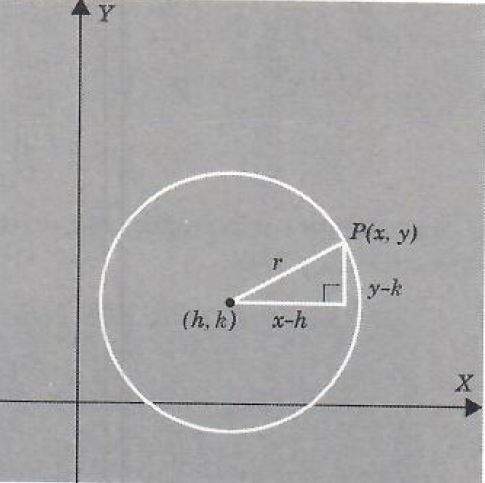
FIGURE 7.
Example 1.
Obtain an equation for the circle having its center at (-1,3/2) and a radius of 2.
Substituting into (1) we obtain
(x-(-1)^2)+(y-3/2)^2=2^2
which simplifies to
(x+1)^2+(y-3/2)^2=4
This is a convenient form in which to leave the equation, since it readily yields the radius and the coordinates of the center.
Consider the equation
(1) Ax^2+Ay^2+Bx+Cy+D=0, A!=0
We recall from Section 6.7 that by using the method of completing the square, this equation can be written in the form
(2) (x-h)^2+(y-k)^2=r^2
We recognize from the form of (2) that its graph, and hence the graph of (1), is the circle with center (h, k) and radius r.
Example 2.
Graph 2x^2+2y^2-3x+4y-3=0
Completing the square we have
x^2+y^2-3/2x+2y-3/2=0
x^2-3/2x+y^2+2y=3/2
x^2-3/2x+9/16+y^2+2y+1=3/2+9/16+1
(x-3/4)^2+(y+1)^2=49/16
(x-3/4)^2+(y+1)^2=(7/4)^2
From this last equation we recognize that its graph is the circle with center (3/4,-1) and radius 7/4.
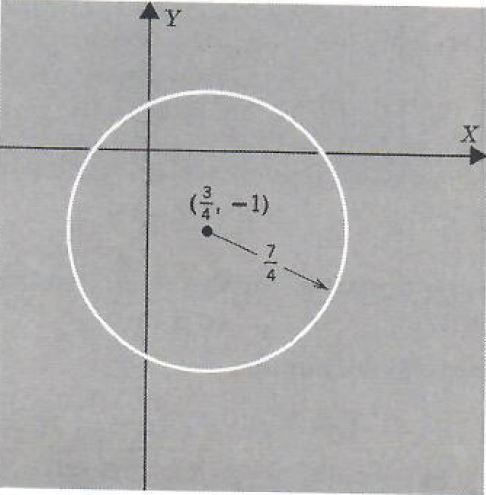
Let's see how our graph generator solves this problem and similar problems and generate graphs. Click on "Solve Similar" button to see more examples.
7.6 Some Parabolas and Their Equations
In many situations a certain type of curve, called a parabola, appears. For example, the path traced out by a stone thrown into the air (not vertically) is a part of a parabola. The arc of water from a hose is a part of a parabola. The reflecting mirror in a car headlight is in the shape of a parabolic dish, and so are the mirrors in a good reflecting telescope.
In a coordinate plane, parabolas are graphs of certain types of second degree equations in the variables x and y. An example of such an equation is
(1) y=x^2
Plotting points and graphing we obtain the curve as shown in Figure 8. From the equation we can tell that as x increases positively or negatively y increases positively. The point at which the parabola turns most sharply is its vertex. The vertex of the parabola in Figure 8 is the point (0,0). This parabola opens upward and the vertical line through its vertex divides it into mirror image halves. This line is called the axis of symmetry of the parabola.
The parabola y=x^2 is just one of the many parabolas with vertical axis and vertex at the origin. In fact, these parabolas are the graphs of equations of the form
(2) y=ax^2
where a is a nonzero real number. If a is positive, then the parabola opens upward. while if a is negative it opens down. To sketch the
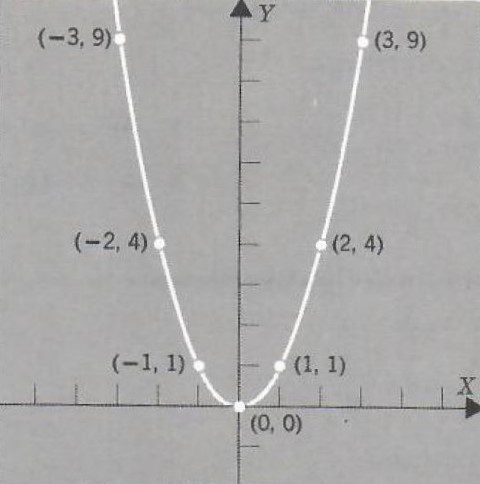
FIGURE 8.
| x | y |
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
graph of a parabola it is usually sufficient to plot the vertex and two or three points on each side of the axis of symmetry.
Example 1 Graph y=-(1/2)x^2.
This is a parabola with vertex at the origin and the Y axis as its axis of symmetry. Since the coefficient -1/2 is negative, the parabola opens downward.
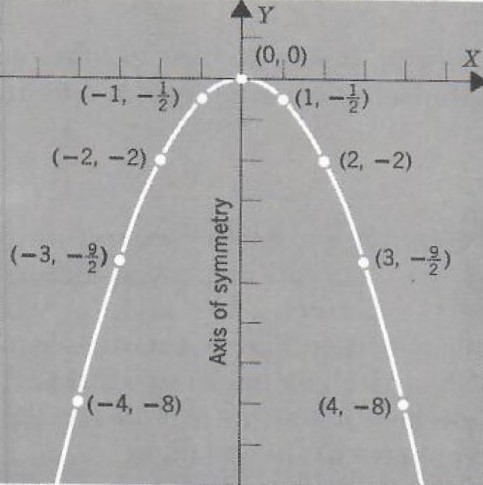
| x | y |
| -4 | -8 |
| -3 | -9/2 |
| -2 | -2 |
| -1 | -1/2 |
| 0 | 0 |
| 1 | -1/2 |
| 2 | -2 |
| 3 | -9/2 |
| 4 | -8 |
Equations of the form
(3) y-k=a(x-h)^2
also have graphs that are parabolas. In fact, they are parabolas with vertex at the point (h,k) and whose axis of symmetry is the vertical line through (h,k). They open up or down depending on whether a is positive or negative.
Example 2. Graph y-3=1/3(x+1)^2.
This is a parabola with vertex at (-1,3) which opens up. Its axis of symmetry is the line x=-1.
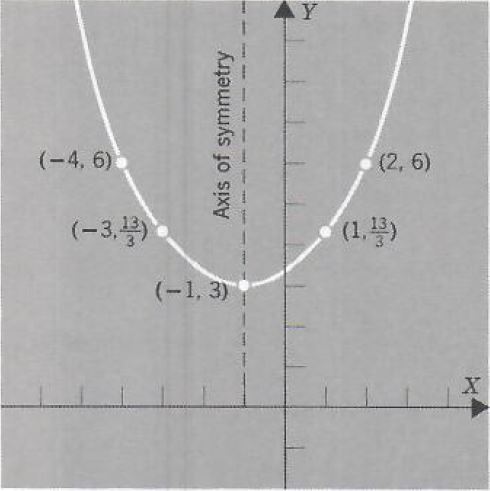
| x | y |
| -4 | 6 |
| -3 | 13/3 |
| -2 | 10/3 |
| -1 | 3 |
| 0 | 10/3 |
| 1 | 13/3 |
| 2 | 6 |
| 3 | 25/3 |
Consider an equation of the form
(4) y=ax^2+bx+c
By completing the square we can transform this equation to one of the form (3) above. Thus the graph of (4) is a parabola. From the resulting equation we can determine the vertex, axis of symmetry, and the direction in which the parabola opens.
Example 3. Graph y=2x^2+3x-1.
We complete the square on the right-hand side
y=2x^2+3x-1
=2(x^2+3/2x+9/16)-1-2*9/16
=2(x+3/4)^2-17/8
y+17/8=2(x+3/4)^2
The graph of the resulting equation is seen to be a parabola opening upward with vertex at (-3/4,-17/8) and axis of symmetry the line x=-3/4
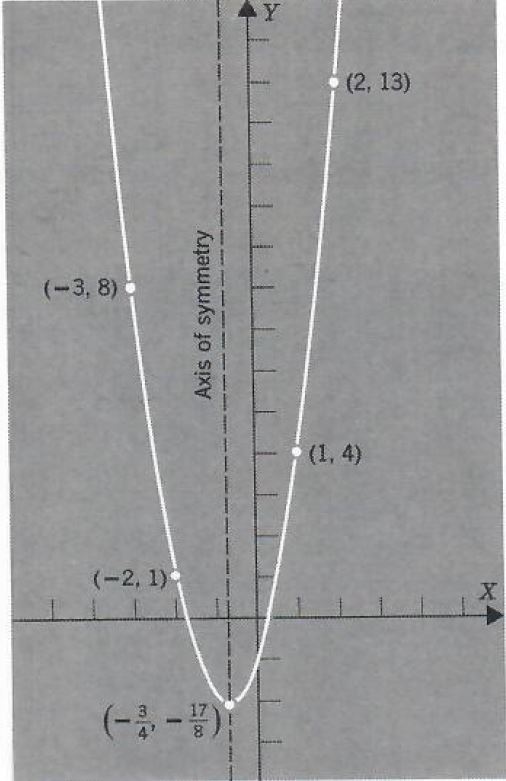
| x | y |
| -2 | 1 |
| -3 | 8 |
| 1 | 4 |
| 2 | 13 |
Similarly, equations of the form
(5) x=ay^2+by+c
have parabolas for graphs. These parabolas have horizontal axes of symmetry and open either to the left or to the right depending on whether a is negative or positive. Again we find the vertex and axis of symmetry by completing the square.
Example 4. Graph x=1/2y^2-2y+3.
x=1/2(y^2-4y)+3
=1/2(y^2-4y+4)+3-2
=1/2(y-2)^2+1
=(x-1)=1/2(y-2)^2
The graph of this equation is a parabola with vertex at (1,2), it opens
to the right, and its axis of symmetry is the line y=2.
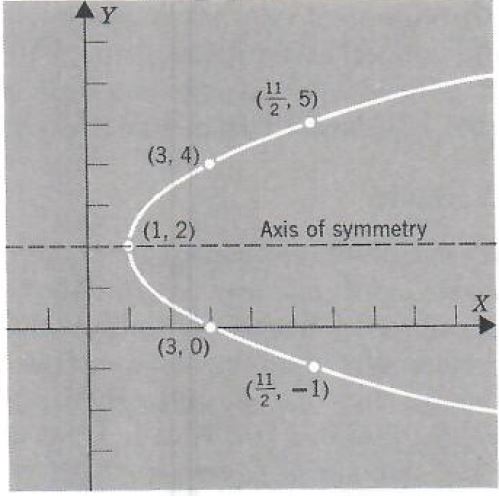
| x | y |
| 11/2 |
--1 |
| 3 | 0 |
| 3/2 | 1 |
| 1 | 2 |
| 3/2 | 3 |
| 3 | 4 |
| 11/2 | 5 |
Let's see how our graph generator solves this problem and similar problems and generate graphs. Click on "Solve Similar" button to see more examples.
Example 5.
Find an equation of the parabola having vertex (3,1), vertical axis of symmetry, and passing through the point P: (2,3).
From equation (3)
y-1=a(x-3)^2
Substituting the coordinates of P we obtain
3-1=a(2-3)^2
a=2
Thus, our equation is
y-1=2(x-3)^2