Ellipse and hyperbola

THE ELLIPSE AND THE HYPERBOLA 

  We have studied two types of second-degree relations thus far: parabolas and circles. We now look at another type, the ellipse.

ELLIPSES   The definition of an ellipse is also based on distance.

ELLIPSES  An ellipse is the set of all points in a plane the sum of whose distances from two fixed points is constant. The two fixed points are called the foci of the ellipse.

  

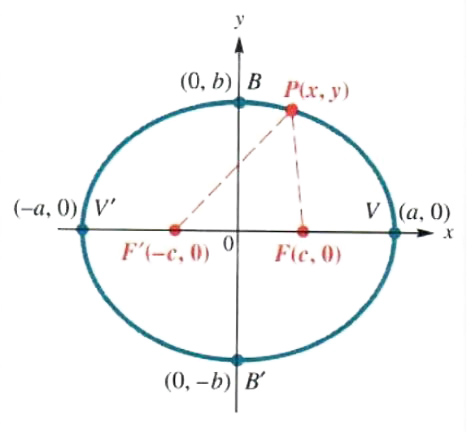
  Figure 3.37

  For example. the ellipse in Figure 3.37 has foci at points F and F '. By the definition, the ellipse is made up of all points P such that the sum d(P, F) + d(R F ’) is constant. The ellipse in Figure 3.37 has its center at the origin. Points V and V ’ are the vertices of the ellipse, and the line segment connecting V and V ’ is the major axis. The foci always lie on the major axis. The line segment from B to B ‘ is the minor axis. The major axis has length 2a, and the minor axis has length 2b.

  If the foci are chosen to be on the x-axis (or y - axis), with the center of the ellipse at the origin, then the distance formula and the definition of an ellipse can be used to obtain the following result. (See Exercise 43.)

EQUATION OF AN ELLIPSE

  The ellipse centered at the origin with x-intercepts a and -a, and y-intercepts b and -b, has equation

  (x^2)/(a^2)+(y^2)/(b^2)=1,

  Where a!=b.

  In an equation of an ellipse, the coefficients of x^2 and y^2 must be different positive numbers. (What happens if the coefficients are equal?)

  An ellipse is the graph of a relation. As suggested by the graph in Figure 3.37, if the ellipse has equation (x^2/a^2) + (y^2/b^2) = 1, the domain is [-a, a] and the range is [-b, b]. Notice that the ellipse in Figure 3.37 is symmetric with respect to the x-axis, the y-axis, and the origin. More generally, every ellipse is symmetric with respect to its major axis, its minor axis, and its center.

  Ellipses have many useful applications. As the earth makes its year-long journey around the sun, it traces an ellipse. Spacecraft travel around the earth in elliptical orbits, and planets make elliptical orbits around the sun. An interesting recent application is the use of an elliptical tub in the nonsurgical removal of kidney stones.

Example 1

GRAPHING AN ELLIPSE CENTERED AT THE ORIGIN

  Graph 4x^2 + 9y^2 = 36.

  To gel the form of the equation of an ellipse, divide both sides by 36.

  (x^2)/9+(y^2)/4=1

  This ellipse is centered at the origin, with x-intercepts 3 and -3, and y-intercepts 2 and -2. Additional ordered pairs that satisfy the equation of the ellipse may be found and plotted as needed (a calculator with a square root key will be helpful). The domain of this relation is -3,3. and the range is -2,2. The graph is shown in Figure 3.38. 

  

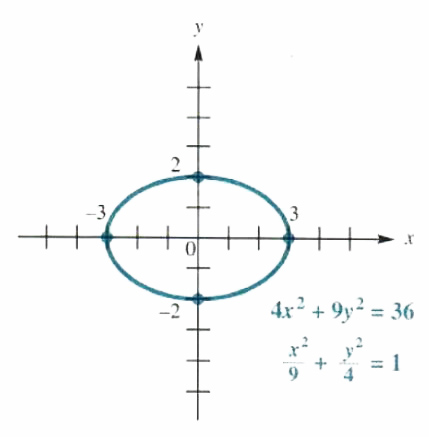
  Figure 3.38

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.  

Example 2

FINDING THE EQUATION OF AN ELLIPSE

  Give the equation of the ellipse with center at the origin, a vertex at (5,0), and minor axis of length 6.

  The equation will have the form (x^2/a^2)+(y^2/b^2)=1. One vertex is at (5,0), so a = 5. The minor axis has length 2b. so

  2b=6

  b=3.

  The equation is

  x^2/25+y^2/9=1

  Recall from Section 3.4 that the circle x^2 + y^2 = r^2, whose center is at the origin, can be translated away from the origin so that the circle (x - h)^2 + (y - k)^2 = r^2 has its center at (h, k). In a similar manner, an ellipse can be translated so that its center is away from the origin.

IN SIMPLEST TERMS

One of the most useful properties of an ellipse is its reflexive property. if a beam is projected from one focus onto the ellipse, it will reflect to the other focus. This feature has helped scientists develop the lithographer, a machine that uses shock waves to crush kidney stones. The waves originate at one focus and are reflected to hit the kidney stone which is positioned at the second focus.

  To determine the focus of an ellipse, use the formula b^2=a^2-c^2, where
the distance from the center to one end of the major axis is represented by a, the distance from the center to one end of the minor axis is represented by b, and the distance from the center to each focus is represented by c. The foci will lie on the major axis. Solving this formula for c gives c=+-root(a^2-b^2).

In finding the foci of the ellipse x^2/25+y^2/9=1, we see that a^2=25,b^2=9 and c=+-root(16)=+-4. Since the center of the ellipse is at (0, 0), the foci are located at (-4, 0) and (4, 0).

Example 3

GRAPHING AN ELLIPSE TRANSLATED AWAY FROM THE ORIGIN

  Graph ((x-2)^2)/(9)+((y+1)^2)/(16)=1 

  If the equation were 

  x^2/9+y^2/16=1,

  

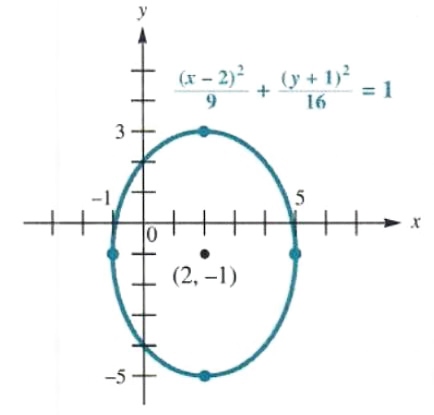
  Figure 3.39

  we would have an ellipse with center at (0, 0). The terms in the numerators of the fractions on the left side, however. indicate that this relation represents an ellipse centered at (2, -1). Graph the ellipse using the fact that a = 3 and b=4. Stan at (2. -1) and locate two points each 3 units away from (2. -1) on a horizontal line, one to the right of (2. -1) and one to the left. Locate two other points on a vertical line through (2. -1), one 4 units up and one 4 units down. Since b > a, the vertices are on the
vertical line through the center. The vertices are (2. 3) and (2. -5). Find additional points as necessary. The final graph is shown in Figure 3.39. As the graph suggests, the domain is -1,5, and the range is -5,3.

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.  

 

HYPERBOLAS  The definition of an ellipse requires that the sum of the distances form two fixed points be constant. The definition of hyperbola involves the difference rather than the sum.

HYPERBOLAS  A hyperbole is the set of all points in a plane such that the absolute value of the difference of the distances from two fixed points (called foci) is constant.

  Some applications of hyperbolas are given in the exercises.

  As with ellipses, the equation of a hyperbola can be found from the distance formula and the definition of a hyperbola. (See Exercise 45.)

EQUATIONS OF HYPERBOLAS 

  A hyperbola centered at the origin, with x-intercepts a and -a, has an equation of the form

  x^2/a^2-y^2/b^2=1,

  while a hyperbola centered at the origin, with y-intercepts b and -b, has an equation of the form

  y^2/b^2-x^2/a^2=1.

  Some texts use y^2/a^2-x^2/b^2=1 for this last equation. For a brief introduction such as this, the form given is commonly used.

  The x-intercepts are the vertices of a hyperbola with the equation (x^2/a^2)-(y^2/b^2)=1, and the y-intercepts are the vertices of a hyperbola with the equation (y^2/b^2)-(x^2/a^2)=1. The line segment between the vertices is the transverse axis of the hyperbola‘ and the midpoint of the transverse axis is the center of the hyperbola.

Example 4

GRAPHING A HYPERBOLA CENTERED AT THE ORIGIN

  Graph the hyperbola x^2/16-y^2/9=1.

  By the first equation of a hyperbola given earlier. the hyperbole is centered at the origin and has x-intercepts 4 and -4. However, if x = 0,

  -y^2/9=1  or  yy^2=-9,

  which has no real solutions. For this reason, the graph has no y-intercepts. To complete the graph. find some other ordered pairs that belong to it. For example, if x=6,

  6^2/16-y^2/9=1  Let x=6.

  -y^2/9=1-39/16  Subtract 36/16

  y^2/9=20/16  Multiply by -1 and combine terms.

  y^2=180/16=45/4  Multiply by 9; lowest terms.

  y=+-(3root(5))/(2)≈ +-3.4.  Take square roots and use a calculator.

  The graph includes the points (6,3.4) and (6, -3.4). If x = -6, y ≈ +-3.4, so the points (-6, 3.4) and (-6, -3.4) also are on the graph. These points, along with other points on the graph, were used to help sketch the final graph shown in Figure 3.40. The graph suggests that the domain of this hyperbola is (-∞,-4) {union} (4,∞), while the range is (-∞,∞). Using the tests for symmetry would show that this hyperbola is symmetric with respect to the x-axis, the y-axis, and the origin. 

    

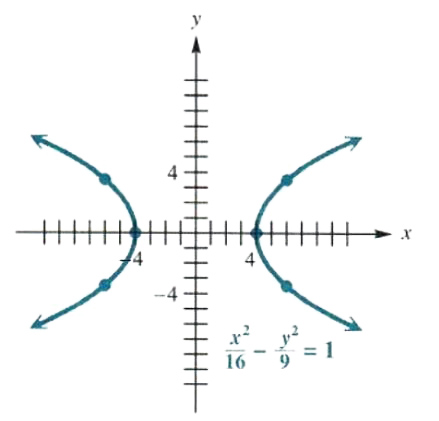
  Figure 3.4

  Starting with

  x^2/a^2-y^2/b^2=1

  and solving for y gives

  x^2/a^2-1=y^2/b^2

  (x^2-a^2)/a^2=y^2/b^2

  y=+-b/(a)root(x^2-a^2)

  If x^2 is very large in comparison to a^2, the difference x^2-a^2 would be very close to x^2. If this happens, then the points satisfying equation (*) above would be very close to one of the lines

  y=+-b/(a)x.

  Thus, as |x| gets larger and larger, the points of the hyperbola x^2/a^2-y^2/b^2=1 come closer and closer to the lines y=(+-b/a)x. These lines, called the asymptotes of the hyperbola, are very helpful when graphing the hyperbola. An asymptotes is a line that the graph of a relation approaches but never reaches as |x| gets large. Asymptotes are discussed again in Sections 5.1 and 6.6.

Example 5

USING ASYMPTOTES TO GRAPH A HYPERBOLA

  Graph x^2/25-y^2/49=1.

  

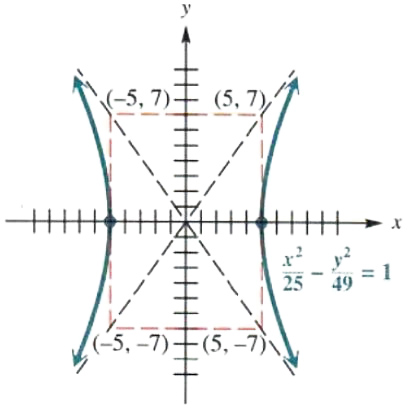
  Figure 3.41  

  For this hyperbola, a = 5 and b = 7. with these values, y = (+-b/a)x becomes y = (+-7/5)x. Use the x-intercepts: if x = 5, then y = (+-7/5)(5) = +-7, and if x = -5, y = 17. These four points, (5, 7),(5, -7), (-5, 7), and (-5, -7), lead to the rectangle shown in Figure 3.41. The extended diagonals of this rectangle are the asymptotes of the hyperbola. The hyperbola has x-intercepts 5 and -5. The domain is (-∞,-5) {union} (5,∞), and the range is (-∞,∞). The final graph is shown in Figure 3.41. 

  The rectangle used to find the asymptotes of the hyperbola in Example 5 is called the fundamental rectangle.

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.  

ASYMPTOTES OF A HYPERBOLA

  The asymptotes of the hyperbola with equation

  x^2/a^2-y^2/b^2=1  or  y^2/b^2-x^2/a^2=1

  are the extended diagonals of the fundamental rectangle with vertices at (a, b),(a, -b), (-a, b), and (-a, -b).

  By using slopes of the diagonals of the fundamental rectangle, we can verify that the equations of the diagonals are as follows.

EQUATIONS OF ASYMPTOTES

  The equations of the asymptotes of either of the hyperbolas (x^2/a^2)-(y^2/b^2)=1 or (y^2/b^2)-(x^2/a^2)=1 are

  y=+-b/(a)x.

  Like the relations studied earlier in this chapter, hyperbolas may be translated. The type of translation can be determined from the equation. just as it was with parabolas, circles, and ellipses.

Example 6

GRAPHING A HYPERBOLA TRANSLATED AWAY FROM THE ORIGIN 

  Graph ((y+2)^2)/(9)-((x+3)^2)/(4)=1.

  

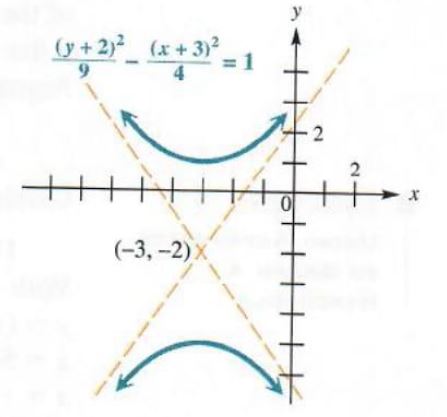
  Figure 3.42

  This hyperbola has the same graph as

  y^2/9-x^2/4=1,

  except that it is centered at (-3, -2). See Figure 3.42. 

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.  

Example 7

FINDING THE EQUATION OF A HYPERBOLA

  Write the equation of the hyperbola centered at (-2, 1), with a vertex at (-2. 3), and with a equal to half of b.

  Since both the vertex and the center are on the transverse axis, it must be the vertical line x = -2. The equation will have the form 

  ((y-1)^2)/(b^2)-((x+2)^2)/(a^2)=1.

  The distance from the center to the given vertex at (-2, 3) gives b for this hyperbola. Using the distance formula,

  b=root((-2+2)^2+(1-3)^2)=2.

  From the information given. a = (1/2)b = (1/2)(2) = 1, so the equation is

  ((y-1)^2)/(4)-((x+2)^2)/(1)=1.

3.6  THE CONIC SECTIONS

  The graphs of the second degree relations studied in this chapter, parabolas, hyperbolas, ellipses, and circles, are called conic sections since each can be obtained by cutting a cone with a plane. as shown in Figure 3.43.

  

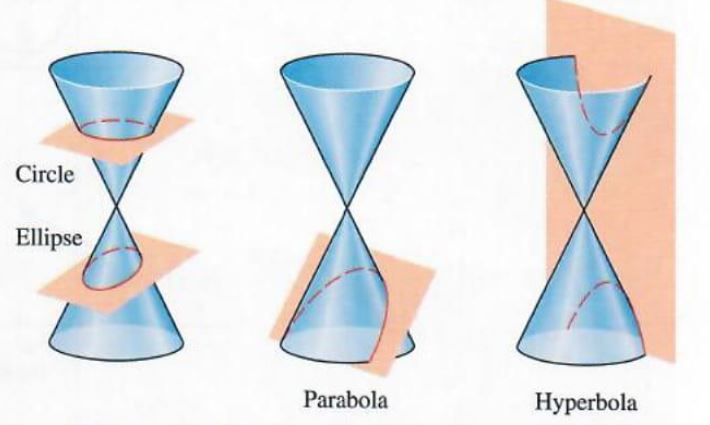
  Figure 3.43

  All conic sections presented in this chapter have equations of the form

  Ax^2+Bx+Cy^2+Dy+{Epsilon}=0,

  where either A or C must be nonzero. The special characteristics of each of the conic sections are summarized below.

EQUATIONS OF CONIC SECTIONS

Conic Section	Characteristic	Example
Parabola	Either A=0 or C=0, but not both.	y=x^2 x=3y^2+2y-4
Circle	A=C!=0	x^2+y^2=16
Ellipse	A!=C,AC>0	x^2/16+y^2/25=1
Hyperbola	AC<0	x^1-y^2=1

  The following chart summarizes our work with conic sections. 

  In order lo recognize the type of graph that a given conic section has, it is sometimes necessary to transform the equation into a more familiar form, as shown in the next examples.

Example 1

DETERMINING THE TYPE OF A CONIC SECTION FROM ITS EQUATION

  Decide on the type of conic section represented by each of the following equations, and sketch each graph.

  (a) 25y^2-4x^2=100.

  Divide each side by 100 to get 

  y^2/4-x^2/25=1.

  This is a hyperbola centered at the origin, with foci on the y-axis, and y-intercepts 2 and -2 The points (5 ,2) (5 ,-2) ,(-5 2) (-5,-2) determine the fundamental rectangle. The diagonals of the rectangle are the asymptotes, and their equations are

  y=+-2/5x.

  The graph is shown in Figure 3.44

  

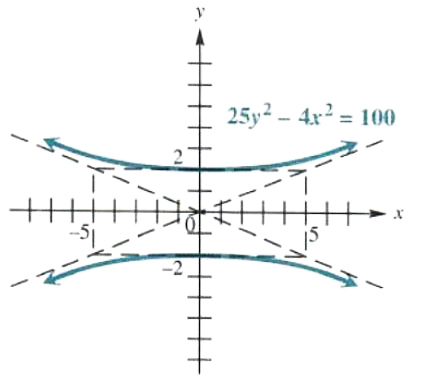
  Figure 3.44

  (b) x^2=25+5y^2

  Rewriting the equation as

  x^2-5y^2=25

  or  x^2/25-y^2/5=1

  shows that the equation represents a hyperbola centered at the origin, with asymptotes

  y=+-b/(a)x

  or  y=(+-root(5))/(5)x

  The x-intercepts are +-5; the graph is shown in Figure 3.45.

  

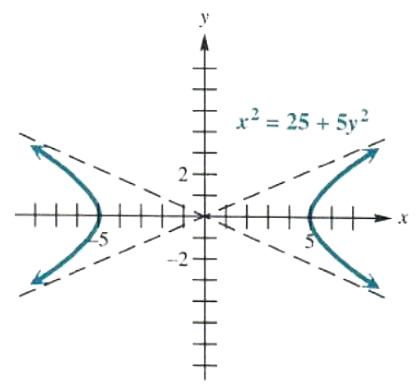
  Figure 3.45

  (c) 4x^2-16x+9y^2+54y=-61

  Since the coefficients of the x^2 and y^2 terms are unequal and both positive, this equation might represent an ellipse. (It might also represent a single point or no points at all.) To find out, complete the square on x and y.

  4(x^2-4x)+9(y^2+6y)=-61  Factor out a 4; Factor out a 9.

  4(x^2-4x+4-4)+9(y^2+6y+9-9)=-61  Add and subtract the same quantity.

  4(x^2-4x+4)-16+9(y^2+6y+9)-81=-61  Regroup and distribute.

  4(x-2)^2+9(y+3)^2=36  Add 97 and factor.

  ((x-2)^2)/9+((y+3)^2)/4=1  Divide by 36.

  This equation represents an ellipse having center at (2, -3) and graph as shown in Figure 3.46.

  

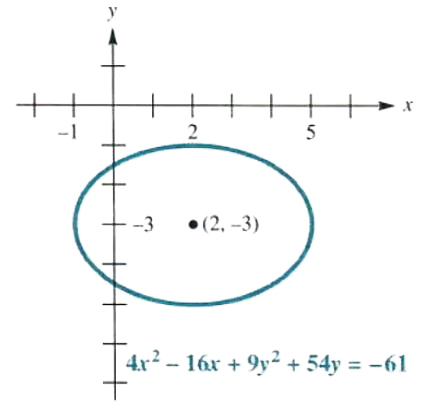
  Figure 3.46

  (d) x^2-8x+y^2+10y=-41

  Complete the square on both x and y, as follows

  (x^2-8x+16)+(y^2+10y+25)=-41+16+25

  (x-4)^2+(y+5)^2=0.

  This result shows that the equation is that of a circle of radius 0; that is, the point (4, -5). Had a negative number been obtained on the right (instead of 0), the equation would have represented no points at all, and there would be no graph.

  (e) x^2-6x+8y-7=0

  Since only one variable is squared (x, and not y), the equation represents a parabola. Rearrange the terms to get the term with y (the variable that is not squared) alone on one side. Then complete the square on the other side of the equation.

  8y=-x^2+6x+7

  8y=-(x^2-6x)+7  Regroup and factor out -1.

  8y=-(x^2-6x+9)+7+9  Add 0 in the form -9 + 9.

  8y=-(x-3)^2+16  Factor.

  y=-1/8(x-3)^2+2  Multiply both sides by 1/8.

  The parabola has vertex at (3, 2), and opens downward, as shown in Figure 3.47. 

  

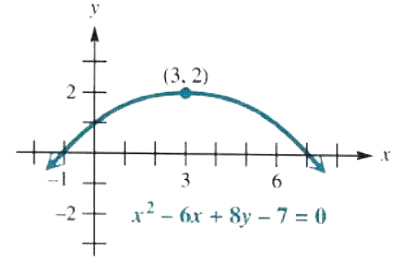
  Figure 3.47

DETERMINING THE TYPE OF A CONIC SECTION FROM ITS EQUATION

  Graph 4y^2-16y-9x^2+18x=-43.

  Complete the square on x and on y.

  4(y^2-4y)-9(x^2-2x)=-43

  4(y^2-4y+4)-9(x^2-2x+1)=-43+16-9

  4(y-2)^2-9(x-1)^2=-36

  Because of the -36, it is very tempting to say that this equation does not have a graph. However, the minus sign in the middle on the left shows that the graph is that of a hyperbola. Dividing through by --36 and rearranging terms gives

  ((-1)^2)/(4)-((y-2)^2)/(9)=1

  a hyperbola centered at (1 , 2), with graph as shown in Figure 3.48. 

  

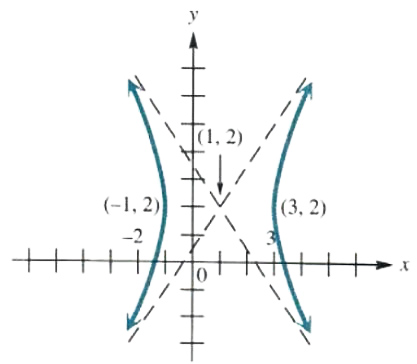
  Figure 3.48

  Relations are sometimes defined as square roots of expressions so that their graphs consist of only a portion of the graph of a complete conic section. The final example illustrates one such relation.

Example 3

GRAPHING A RELATION DEFINED BY A SQUARE ROOT

  Graph y=-root(1+4x^2)

  Squaring both sides gives

  y^2=1+4x^2

  or  y^2-4x^2=1

  Use the fact that 4 = 1/(1/4) to write the equation as

  y^2/1-x^2/(1/4)=1

  the equation of a hyperbola with y-intercepts 1 and -1. Use the points (1/2, 1),(1/2, -1), (-1/2, 1), and (-l/2, -1) to sketch the asymptotes. Since the given equation y=-root(1+4x^2) restricts y to nonpositive values, the graph is the lower branch of the hyperbola, as shown in Figure 3.49. The domain of y=-root(1+4x^2) is the set of all x such that 1+4x^2>=0. This condition is satisfied for all x in the interval (-∞,∞). The range is (-∞,-1). 

  

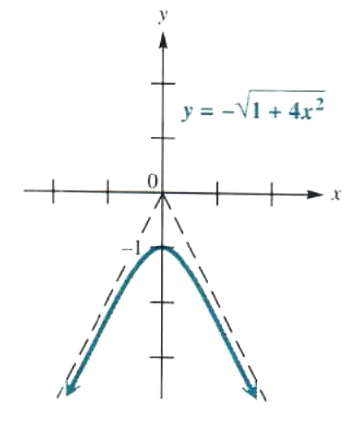
  Figure 3.49

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.